5 назовите математические растения

Математика в природе: самые красивые закономерности в окружающем мире

От радуг, речных изгибов и теней до паутины, сот и отметин на шкурах животных — видимый мир полон закономерностей, которые можно описать математически. Рассказываем о самых интересных из них.

Читайте «Хайтек» в

Математика в природе

Первые древнегреческие философы пытались описать и объяснить порядок в природе, предугадывая современные идеи. В своих работах о закономерностях природы Платон (около 427–347 до н. э.) писал о существовании универсалий. Он предполагал, что они состоят из идеальных форм (др.-греч. εἶδος, форма), а физические объекты — это не более чем несовершенные копии. Таким образом, цветок может быть примерно круглым, но это никогда не будет идеальный круг . Пифагор рассматривал закономерности в природе, так же, как и гармонии в музыке, берущими начало из числа, как первоначала всего сущего . Эмпедокл в какой-то степени предвосхитил эволюционное объяснение структуры организмов Дарвина .

В 1202 году Леонардо Фибоначчи открыл последовательность чисел Фибоначчи западному миру в своей «Книге абака» . Фибоначчи привел (несуществующий) биологический пример численного роста теоретической популяции кроликов . В 1917 году Дарси Томпсон (1860–1948) опубликовал свою книгу «О росте и форме». Его описание взаимосвязи филлотаксиса (расположения листьев на стебле растения) и чисел Фибоначчи (математическое отношение закономерностей спирального роста в растениях) стало классическим. Он показал, что простые уравнения могут описать все с виду сложные закономерности спирального роста рогов животных и раковин моллюсков .

Тюринг, Плато, Геккель, Цейзинг — знаменитые деятели искусства и науки — искали строгие законы математики и находили ее в красоте природы.

Спираль Фибоначчи — геометрическая прогрессия красоты

Спирали распространены среди растений и некоторых животных, особенно среди моллюсков. Например, у моллюсков-наутилид каждая ячейка их раковины — примерная копия следующей, масштабированная константой и выложенная в логарифмическую спираль.

Чаще всего в природе встречается последовательность Фибоначчи. Она начинается с чисел 1 и 1, а затем каждое последующее число получается путем сложения двух предыдущих чисел. Следовательно, после 1 и 1 следующее число — 2 (1 + 1). Следующее число — 3 (1 + 2), затем 5 (2 + 3) и так далее.

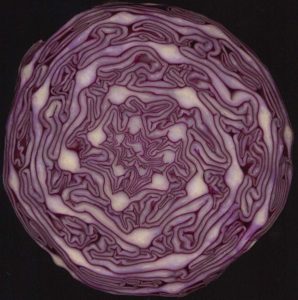
Спирали в растениях наблюдаются в расположении листьев на стебле, а также в структуре бутона и семян цветка — например, у подсолнуха или структуры плода ананаса и салака. Последовательность Фибоначчи можно заметить и у сосновой шишки, где огромное количество спиралей расположено по часовой и против часовой стрелки. Эти механизмы объясняются по-разному — математикой, физикой, химией, биологией. Каждое из объяснений верно само по себе, но необходимо учитывать их все .

С точки зрения физики, спирали — конфигураций низких энергий, которые возникают спонтанно путем самоорганизации процессов в динамических системах. С точки зрения химии, спираль может быть образована реакционно-диффузионным процессом с привлечением как активации, так и ингибирования. Филлотаксис контролируется протеинами, которые управляют концентрацией растительного гормона ауксина, который активирует рост среднего стебля наряду с другими механизмами контроля относительного угла расположения бутона к стеблю. С точки зрения биологии листья расположены настолько далеко друг от друга, насколько позволяет естественный отбор, так как он максимизирует доступ к ресурсам, особенно к солнечному свету, для фотосинтеза.

Фракталы — бесконечное (почти) повторение

Фракталы — еще одна интересная математическая форма, которую каждый видели в природе. Сам Фрактал — это самоподобная повторяющаяся форма, что означает, что одна и та же основная форма появляется снова и снова. Другими словами, если вы увеличите или уменьшите масштаб, везде будет видна одна и та же.

Эти самоподобные циклические математические конструкции, обладающие фрактальной размерностью, встречаются довольно часто, особенно среди растений. Самый известный пример — папоротник.

Кстати, бесконечная повторяемость невозможна в природе, поэтому все фрактальные закономерности — это только аппроксимации (приближения). Например, листья папоротников и некоторых зонтичных растений (например, тмин) являются самоподобными до второго, третьего или четвертого уровня.

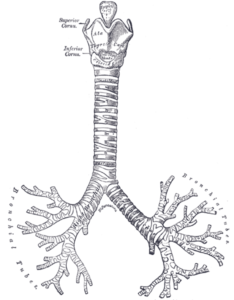
Схожие с папоротником паттерны встречаются также у многих растений (брокколи, капуста сорта Романеско, кроны деревьев и листья растений, плод ананаса), животных (мшанки, кораллы, гидроидные, морские звезды, морские ежи). Также фрактальные паттерны имеют место в структуре разветвления кровеносных сосудов и бронхов животных и человека.

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференцируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введен Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.

Многоугольники — инженерный гений

При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники.

Например, соты, в которых пчелы хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и как-то координируют свои попытки сделать соты одинаковыми.

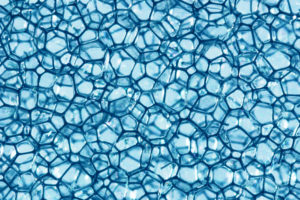
Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов. Почему так происходит?

Пена — это множество пузырей. В природе существуют пенопласты из разных материалов. Пена, состоящая из мыльных пленок , подчиняется законам Плато, согласно которым три мыльные пленки соединяются под углом 120 градусов, а четыре грани соединяются в каждой вершине тетраэдра под углом 109,5 градусов. Затем по законам Плато требуется, чтобы пленки были гладкими и непрерывными, а также имели постоянную среднюю кривизну в каждой точке. Например, пленка может оставаться почти плоской в среднем, имея кривизну в одном направлении (например, слева направо), и в то же время искривляться в обратном направлении (например сверху вниз). Лорд Кельвин сформулировал задачу упаковки клеток одного объема наиболее эффективным способом в виде пены в 1887 году; его решение — кубическая сота со слабо изогнутыми гранями, удовлетворяющими законам плато. До 1993 года это решение оставалось лучшим, пока Денис Ваэрен и Роберт Фэлан не предложили структуру Ваэра-Фэлена . Впоследствии эта структура была адаптирована для внешней стены Пекинского национального плавательного комплекса, построенного для проведения летних Олимпийских игр 2008 года .

Природа озабочена экономией. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.

Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.

Читать далее

Источник

Назовите математические растения?

Назовите фамилию ученого, одного из основателей математической логики, в честь которого назван катер на Луне?

Назовите фамилию ученого, одного из основателей математической логики, в честь которого назван катер на Луне?

Математическое действие?

Назови математические классы , назови разряды всех классов , назови все правила на умножение и деление 0 и 1?

Назови математические классы , назови разряды всех классов , назови все правила на умножение и деление 0 и 1.

Математическая сказка?

Математическая сказка?

Математические ребусы?

Назовите Часть растения которые растут на побегах с их помощью растения питается и дышит?

Назовите Часть растения которые растут на побегах с их помощью растения питается и дышит.

Математическая сказка?

Математическое действие?

Вы зашли на страницу вопроса Назовите математические растения?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

— 823855 Поставь луйс Пожалюйста.

Под буквой А, а рпавельней : а — в + а + с.

Тут графики корень(1. 3, 0) в первом.

23 / 5 * 4 / 9 + 4 / 9 * 22 / 5 = 92 / 45 + 88 / 45 = 180 / 45 = 4.

30 минут = 0, 5часа1 : 0, 5 = 2км / чответ : 2 км / ч.

30 : 1 = 30(км|м. ) Ответ : скорость пешехода 30 км ч.

Вероятность вынуть синий кубик : 3 / (5 + 12 + 3) = 3 / 20 вероятность выпадения 5 : 1 / 6 вероятность искомая : 3 / 20 * 1 / 6 = 1 / 40 Ответ : 1 / 40.

Обозначим сумму всех чисел таблицы через S, а незакрашенное число через N. По условию S = 2708. Пусть сумма 12 синих чисел равна , а сумма 12 красных , тогда + = + 4 = 5. Т. е. S = 5 + N. Видим, что S и N должны давать одинаковые остатки от де..

© 2000-2023. При полном или частичном использовании материалов ссылка обязательна. 16+
Сайт защищён технологией reCAPTCHA, к которой применяются Политика конфиденциальности и Условия использования от Google.

Источник

5 назовите математические растения

Ученые узнали, что растения с математической точностью рассчитывают запасы крахмала, которых должно хватить, чтобы пережить ночь, сообщает «TG Daily».

«Это первый пример фундаментальных биологических процессов с такими сложными арифметическими вычислениями, которые мы увидели», говорит профессор из Центра Джона Иннеса Мартин Говард.

Растения питаются в течение дня, за счет энергии солнца, преобразовывая углекислый газ в крахмал и сахар. Как только солнце садится, они зависят только от запасов крахмала.

Результаты исследования опубликуют в журнале eLife. В нем говорится о том, как растения поразительно точно регулируют скорость потребления крахмала. Эти корректировки гарантируют, что запаса крахмала хватит до рассвета, даже если неожиданно пропадет источник света или изменится запас крахмала.

Ученые из центра Джона Иннеса говорят, что для того чтоб регулировать запас крахмала так точно растения должны выполнять сложные математические расчеты.

«Возможность выполнять арифметические вычисления, жизненно необходимы для роста и урожайности растения», говорит биолог Элисон Смит.

Понимания того, как растения растут в темноте, поможет открыть новые способы повышения урожайности.

Ночью механизм внутри листьев измеряет запас крахмала и оценивает, сколько времени осталось до рассвета. Информация о времени поступает во внутренние часы, которые похожи на наши биологические часы. Размер запаса крахмала делится на отрезок времени до наступления рассвета, для того чтобы установить правильную скорость потребления, так чтобы на рассвете было использовано около 95% запаса крахмала.

«Расчеты настолько точно что растения не только не испытывают голод но и наиболее эффективно используют свою пищу», говорит Смит.

«Если запасы крахмала будут использоваться слишком быстро, то растение будет голодать и перестанет расти ночью, а если слишком медленно, то часть крахмала будет потрачена впустую».

Ученые с помощью математического моделирования выяснили, как такое вычисление происходит внутри растения. Они предположили, что информация о размере запаса крахмала и времени до рассвета кодируется в виде двух молекул (S – крахмал, Т — время). Если молекула S стимулирует потребление крахмала, то молекула T ограничивает темп потребления, то есть S делим на T.

—>Категория : Растения | —>Добавил : mykar (24.06.2013)

Источник