6 класс схемы графы деревья

Страница 203 параграф 13 Работа 14 задание №1, ГДЗ по информатике за 6 класс к учебнику Босовой

§13. Схемы. Создаём информационные модели — схемы, графы и деревья. Страница 203 §13 Работа 14 задание №1

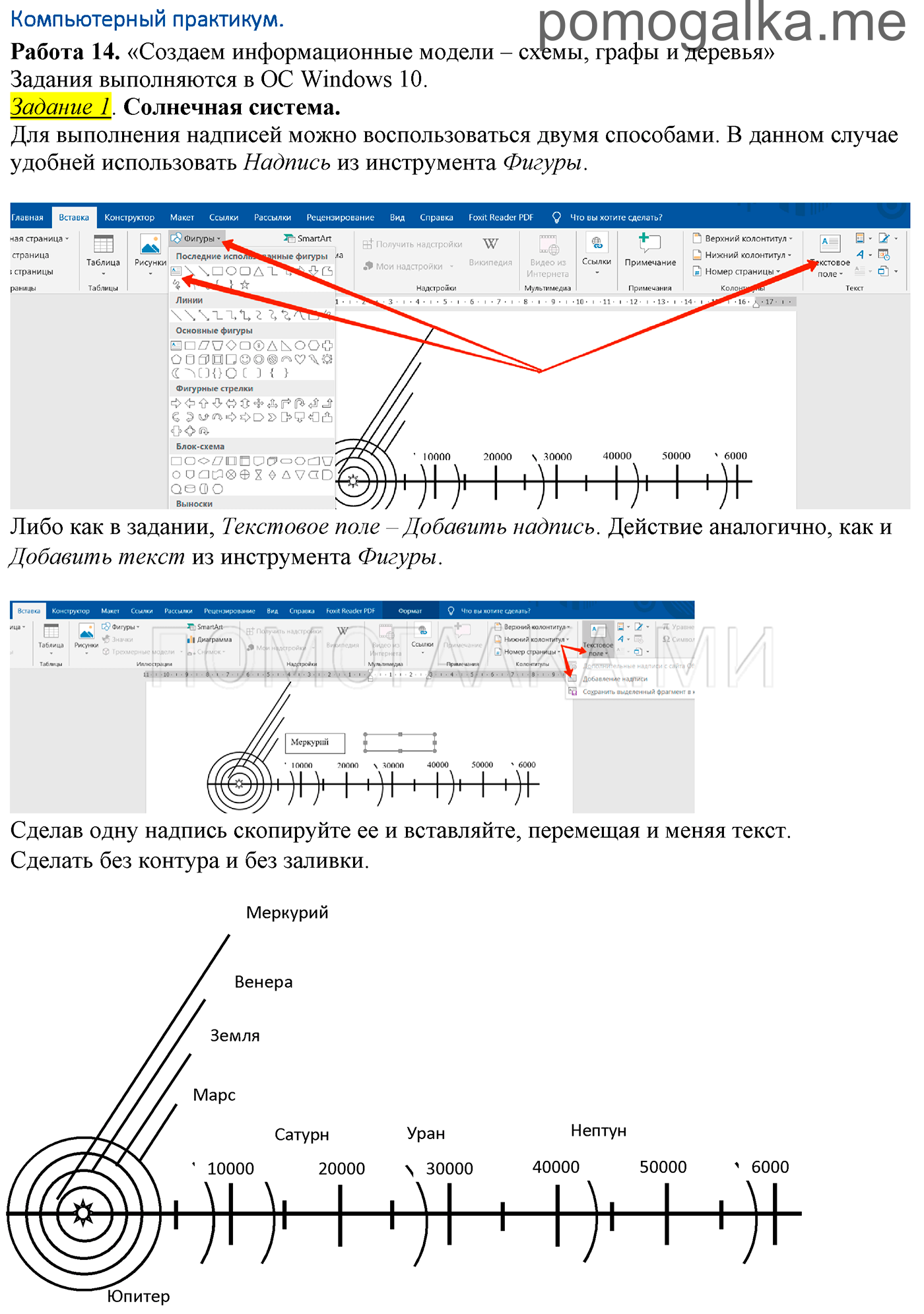
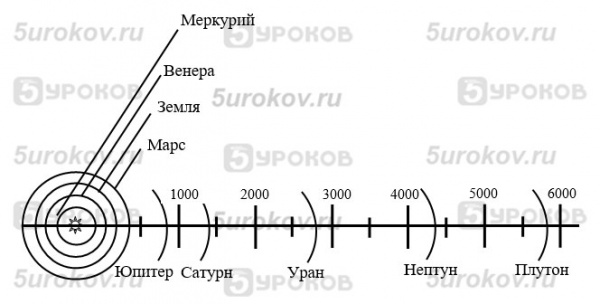
Задание 1. Солнечная система. Работа 14. Создаем информационные модели – схемы, графы и деревья
Для выполнения надписей можно воспользоваться двумя способами. В данном случае удобней использовать Надпись из инструмента Фигуры.
Либо как в задании, Текстовое поле – Добавить надпись. Действие аналогично, как и Добавить текст из инструмента Фигуры.
Сделав одну надпись скопируйте ее и вставляйте, перемещая и меняя текст.
Сделать без контура и без заливки.

Источник

Страница 206 параграф 13 Работа 14 задание №6, ГДЗ по информатике за 6 класс к учебнику Босовой

§13. Схемы. Создаём информационные модели — схемы, графы и деревья. Страница 206 §13 Работа 14 задание №6

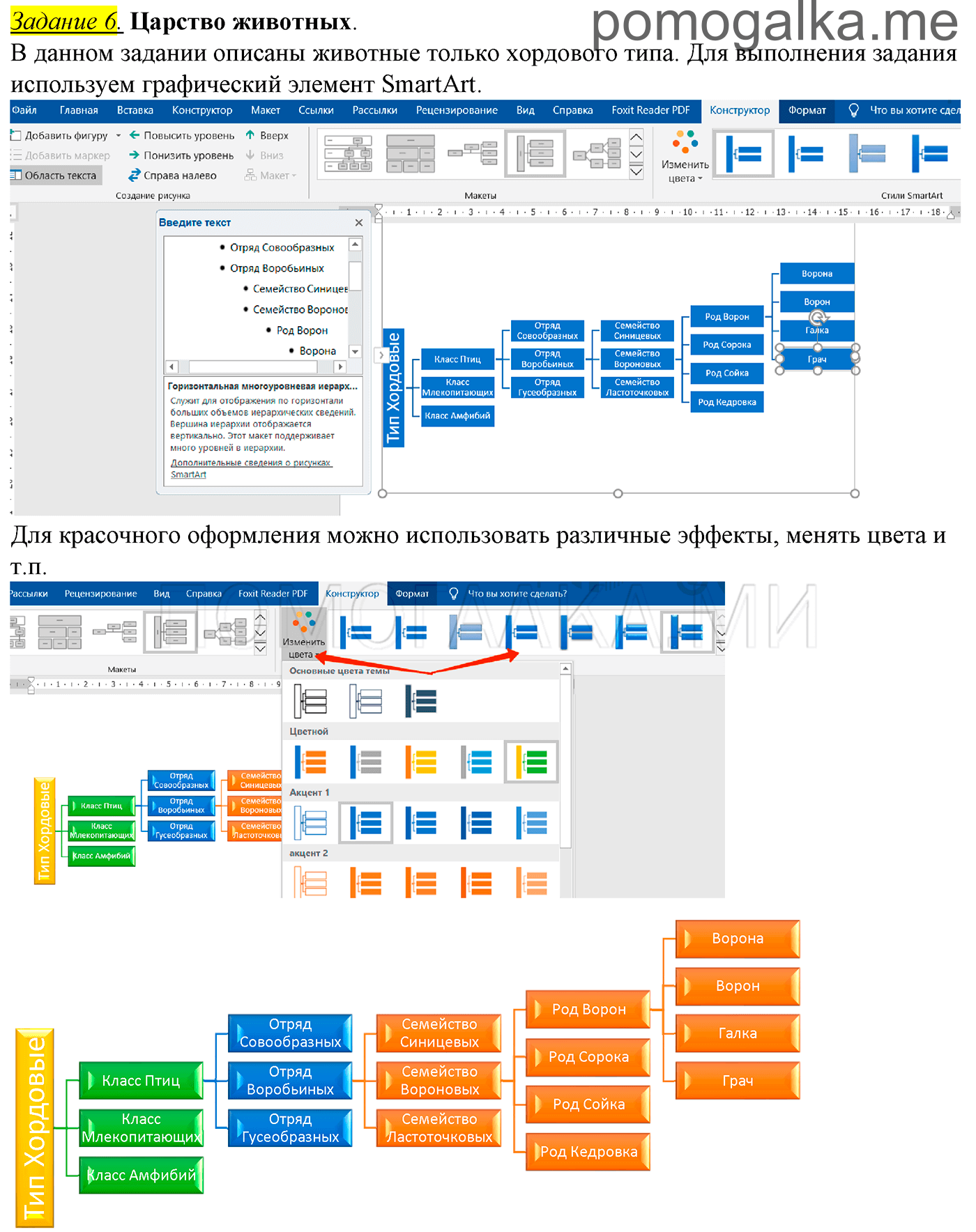
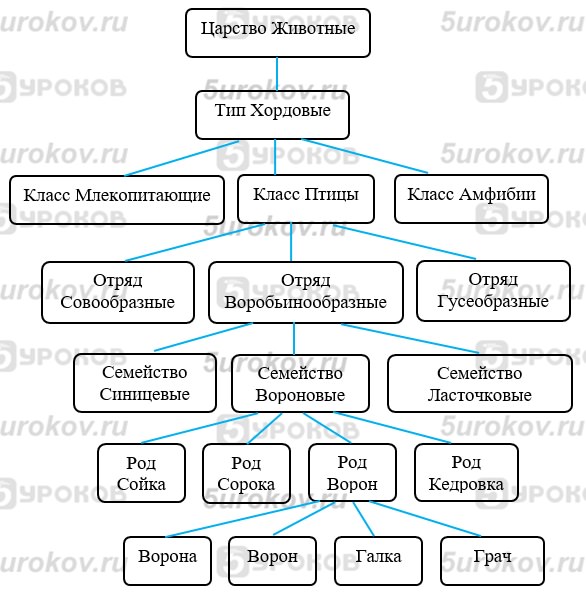
Задание 6. Царство животных 14. Создаем информационные модели – схемы, графы и деревья
В данном задании описаны животные только хордового типа. Для выполнения задания используем графический элемент SmartArt.
Для красочного оформления можно использовать различные эффекты, менять цвета и т.п.

Источник

Страница 204 параграф 13 Работа 14 задание №2, ГДЗ по информатике за 6 класс к учебнику Босовой

§13. Схемы. Создаём информационные модели — схемы, графы и деревья. Страница 204 §13 Работа 14 задание №2

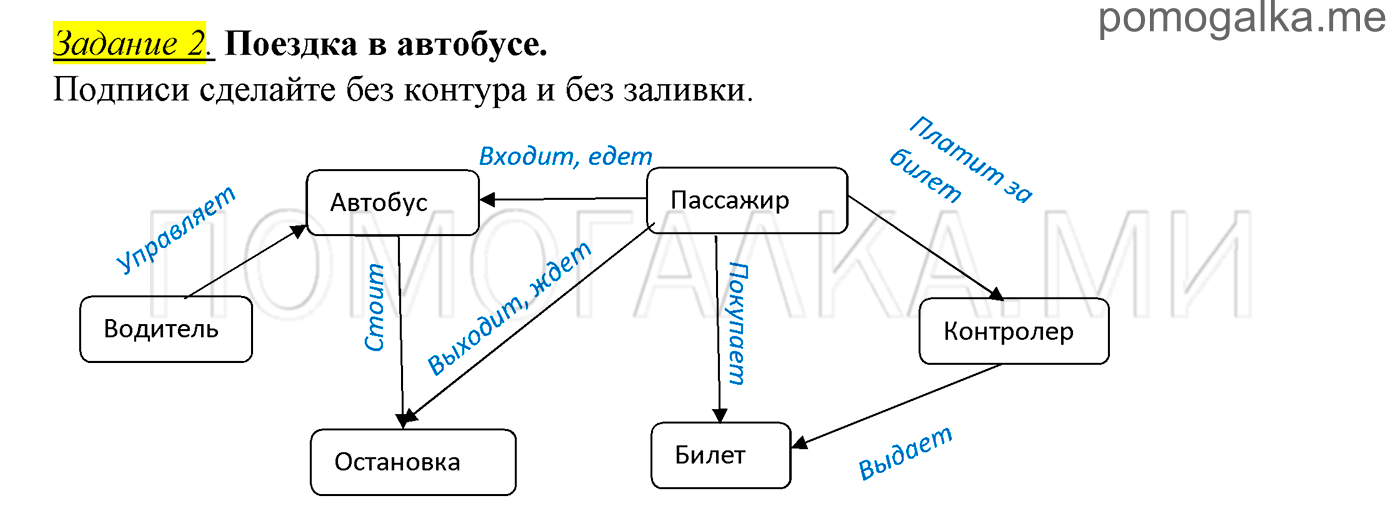
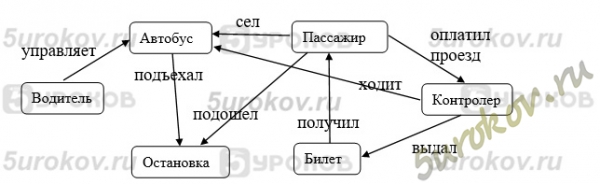
Задание 2. Поездка в автобусе. Работа 14. Создаем информационные модели – схемы, графы и деревья
Подписи сделайте без контура и без заливки.

Источник

Работа 14 Создаём информационные модели — схемы, графы и деревья

Задание 1. Солнечная система

Задание 2. Поездка в автобусе

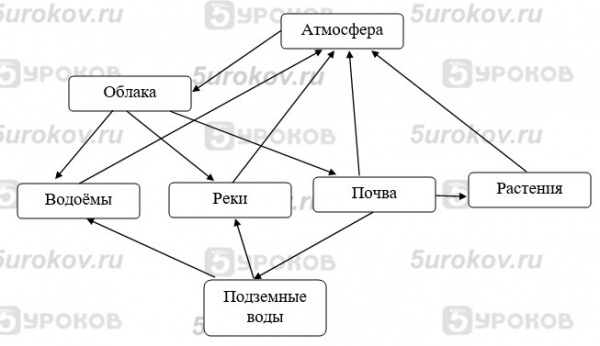
Задание 3. Круговорот воды в природе

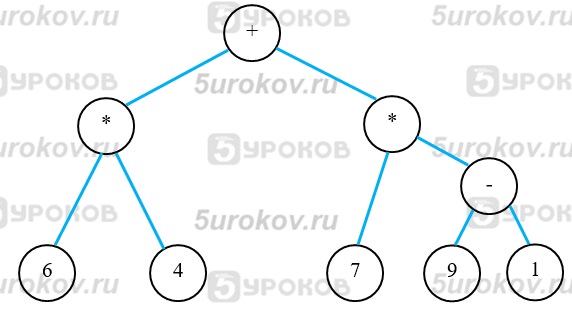
Задание 4. Арифметические выражения
Постройте дерево для арифметического выражения 6 * 4 + 7 * (9 – 1)

Задание 6. Царство животных
Составьте схему по следующему описанию. (Описание в учебнике)

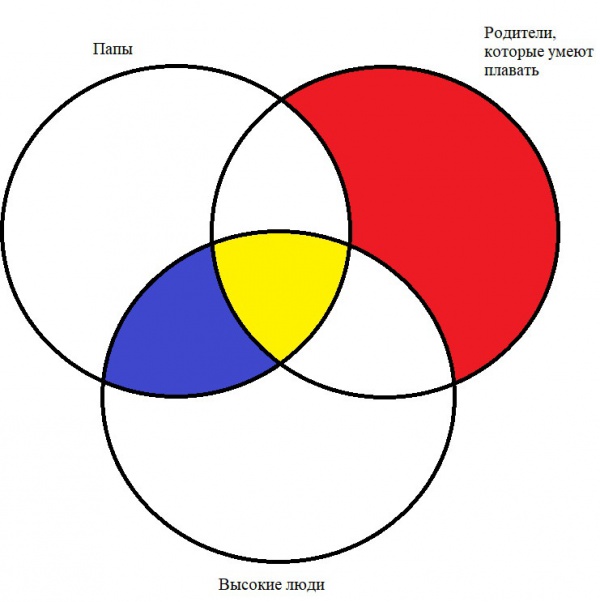
Задание 7. Круги Эйлера
Постройте схему, на которой кругами обозначьте три множества: множество всех высоких людей; множество всех пап; множество родителей, умеющих плавать. Подпишите эти множества.
Желтый цвет — множество всех высоких пап, умеющих плавать.
Синий цвет — множество всех высоких пап, не умеющих плавать.
Красный цвет — множество всех невысоких мам, умеющих плавать.

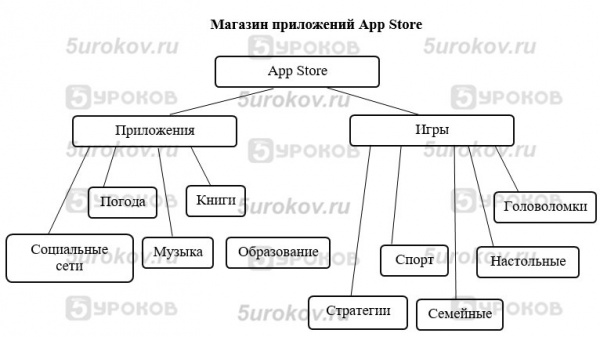
Задание 8. Творческое задание
Мы составили схему магазина приложений App Store.

Источник

Схемы

В повседневной жизни нас окружает множество разнообразных схем: схемы проезда, схемы дорожных развязок, схема метрополитена, схема расположения мест в зрительном зале, схема движения пригородных электропоездов и многие другие.

Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схемы может быть представлен и внешний вид объекта, и его структура.

Например, внешний вид зрительного зала представлен на схеме, изображённой на рис. 40. Представление о внешнем виде квартиры можно получить по схеме на рис. 41.

Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта. На карте (рис. 42) изображён внешний вид территории северо-восточной части Центральной России. На ней показаны древние русские города, образующие знаменитое на весь мир Золотое кольцо.

Схемы на рис. 40-42 являются информационными моделями внешнего вида соответствующих объектов. Они предназначены для того, чтобы у человека была возможность, например, выбрать подходящее место в зрительном зале, оценить размеры и расположение комнат будущей квартиры, разработать маршрут путешествия по Золотому кольцу и т. д. Для этих моделей большое значение имеет соблюдение масштаба. Для карты также имеет значение соблюдение ориентации по сторонам света. Но, несмотря на точность рассмотренных информационных моделей, более подробные сведения об изображённых на них объектах (местах в зале, домах, дорогах, городах) из них получить нельзя.

Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта.

Например, туристический маршрут «Золотое кольцо России» более образно запечатлен на схеме на рис. 43.

Здесь не полностью выдержан масштаб, но зато акцентировано внимание на городах, образующих Золотое кольцо, и их достопримечательностях.

Информационные модели на графах

Наглядным средством представления состава и структуры системы является граф. Граф состоит из вершин, связанных линиями. Если линия направленная (со стрелкой), то она называется дугой; линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей. Вершины могут изображаться кругами, овалами, точками, прямоугольниками и т. д.

Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель рассматриваемой системы в форме графа.

Ранее мы рассматривали графы — схемы отношений, отражающие имеющиеся связи между объектами.

Например, граф, отражающий отношение «переписываются» между объектами класса «дети», может выглядеть, как показано на рис. 44.

Отношение «переписываются» («пишут письма друг другу») является двухсторонним (симметричным). Поэтому соответствующие вершины соединены линиями без стрелок (рёбрами).

Граф называется неориентированным, если его вершины соединены ребрами.

Путь по вершинам и рёбрам графа, включающий любое ребро графа не более одного раза, называется цепью.

Пример цепи: Юра — Аня — Витя — Коля (см. рис. 44).

Цепь, начальная и конечная вершины которой совпадают, называется циклом.

Пример цикла: Аня — Коля — Витя — Аня.

Иначе выглядит граф, отражающий отношение «пишет письма» между теми же объектами класса «дети». Линии со стрелками (дуги) придают ему совершенно иной смысл (рис. 45).

Граф называется ориентированным, если его вершины соединены дугами.

Приведите примеры цепи и цикла в графе на рис. 45.

Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).

На рисунке 46 информация о городах Золотого кольца представлена взвешенным графом: веса его вершин — года основания городов, веса рёбер — расстояния в километрах между городами.

Назовите пути и циклы в графе на рис. 46.

Граф с циклами называется сетью.

На рисунке 47 в виде графа представлена информационная модель сказки про Царевну-лягушку.

Вершины этого графа — персонажи и предметы из сказки, дуги — связи между ними. В отличие от предыдущих примеров,

здесь все связи различны. Поэтому они подписываются рядом с соответствующими дугами.

Такой граф называется семантической сетью. Считается, что любую информацию можно представить в виде семантической сети, на которой будут отражены объекты (понятия) и связи (отношения) между ними.

Деревья

Иерархия — это расположение частей или элементов целого в порядке от высшего к низшему. Системы, элементы которых находятся в отношениях «является разновидностью», «входит в состав» и других отношениях подчинённости, называются иерархическими системами (системами с иерархической структурой).

Например, иерархическую структуру имеет школа, потому что в ней установлены следующие отношения подчинённости: директор — заместители директора — учителя — ученики.

Иерархическую структуру имеют системы, элементы которых связаны отношением «входит в состав».

На рисунке 48 изображён граф иерархической системы, представляющий состав прикладного программного обеспечения (ПО) компьютера.

Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.

Обычно у дерева, представляющего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Каждая вершина дерева (кроме корня) имеет только одного предка — обозначенный ею объект входит в один класс верхнего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один ко многим». Вершины, не имеющие порождённых вершин, называются листьями.

Древовидными являются схемы отношений «является разновидностью», используемые для наглядного представления классификации объектов (рис. 49).

Иерархию легко изобразить «лесенкой» — в виде многоуровневого списка. Объекты одного уровня иерархии располагаются на одном уровне в списке. Чем ниже уровень иерархии, тем правее находится соответствующий уровень списка:

Рептилии
Черепахи
Крокодилы
Клювоголовые
Чешуйчатые
Ящерицы
Змеи

По иерархическому принципу организована система хранения файлов во внешней памяти компьютера. Операционная система позволяет получить на экране компьютера изображение файловой системы в виде дерева (рис. 50).

Родственные связи между членами семьи удобно изображать с помощью схемы, называемой генеалогическим или родословным деревом. Изображать генеалогическое дерево можно в любом направлении — это дело вкуса разработчика модели.

Использование графов при решении задач

Графы удобно использовать при решении некоторых классов задач.

Задача 1

Сколькими способами можно рассадить в ряд на три стула трёх учеников? Выписать все возможные случаи.

Решение этой задачи удобнее всего представить в виде дерева. За его корневую вершину возьмём произвольную точку плоскости О.

На первый стул можно посадить любого из трёх учеников — обозначим их А, В л С. На схеме это соответствует трём ветвям, исходящим из точки О (рис. 51).?

Посадив на первый стул ученика А, на второй стул можно посадить ученика В или С. Если же на первый стул сядет ученик В, то на второй можно посадить А или С. Если на первый стул сядет С, то на второй можно будет посадить А или В. Это соответствует на схеме двум ветвям, исходящим из каждой вершины первого уровня (рис. 52).

Очевидно, что третий стул в каждом случае займёт оставшийся ученик. Это соответствует одной ветви дерева, которая «вырастает» на каждой из предыдущих ветвей (рис. 53).

Выпишем все пути от вершин первого уровня к вершинам третьего уровня: А-В-Су А-С-В, В-А-С, В-С-А, С-А-Б, С-В-А. Каждый из выписанных путей определяет один из вариантов рассаживания учеников на стулья. Так как других путей нет, то искомое число способов — 6.

Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их число. В этом случае рассуждать нужно так: на первый стул можно усадить одного из трёх человек, на второй — одного из двух оставшихся, на третий — одного оставшегося: 3-2-1 = 6.?

Задача 2

Чтобы принести Царю-батюшке молодильные яблоки, должен Иван-царевич найти единственный верный путь к волшебному саду. Встретил Иван-царевич на развилке трёх дорог старого ворона и вот какие советы от него услышал:

1) иди сейчас по правой тропинке;

2) на следующей развилке не выбирай правую тропинку;

3) на третьей развилке не ходи по левой тропинке.

Пролетавший мимо голубь шепнул Ивану-царевичу, что только один совет ворона верный и что обязательно надо пройти по тропинкам разных направлений. Наш герой выполнил задание и попал в волшебный сад. Каким маршрутом он воспользовался?

Обозначим левую, среднюю и правую тропинки соответственно Л, С и П. Возможные маршруты представим в виде графа. При этом подсказки ворона отметим более «жирными» рёбрами. Так как только один совет ворона верен, то на графе ему будет соответствовать маршрут, имеющий одно «жирное» ребро. Этот маршрут обозначен дополнительной пунктирной линией (рис. 54).

Источник