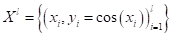Методы классификации и прогнозирования. Деревья решений
На сегодняшний день существует большое число алгоритмов, реализующих деревья решений: CART , C4.5, CHAID, CN2, NewId, ITrule и другие.
Алгоритм CART
Алгоритм CART ( Classification and Regression Tree), как видно из названия, решает задачи классификации и регрессии. Он разработан в 1974-1984 годах четырьмя профессорами статистики — Leo Breiman (Berkeley), Jerry Friedman (Stanford), Charles Stone (Berkeley) и Richard Olshen (Stanford).
Атрибуты набора данных могут иметь как дискретное, так и числовое значение.
Алгоритм CART предназначен для построения бинарного дерева решений . Бинарные деревья также называют двоичными. Пример такого дерева рассматривался в начале лекции.
Другие особенности алгоритма CART :
- функция оценки качества разбиения;
- механизм отсечения дерева;
- алгоритм обработки пропущенных значений;
- построение деревьев регрессии.
Каждый узел бинарного дерева при разбиении имеет только двух потомков, называемых дочерними ветвями. Дальнейшее разделение ветви зависит от того, много ли исходных данных описывает данная ветвь . На каждом шаге построения дерева правило , формируемое в узле, делит заданное множество примеров на две части. Правая его часть ( ветвь right) — это та часть множества, в которой правило выполняется; левая ( ветвь left) — та, для которой правило не выполняется.
Функция оценки качества разбиения, которая используется для выбора оптимального правила , — индекс Gini — был описан выше. Отметим, что данная оценочная функция основана на идее уменьшения неопределенности в узле. Допустим, есть узел, и он разбит на два класса. Максимальная неопределенность в узле будет достигнута при разбиении его на два подмножества по 50 примеров, а максимальная определенность — при разбиении на 100 и 0 примеров.
Правила разбиения. Напомним, что алгоритм CART работает с числовыми и категориальными атрибутами. В каждом узле разбиение может идти только по одному атрибуту. Если атрибут является числовым, то во внутреннем узле формируется правило вида xi внутреннем узле формируется правило xi V(xi), где V(xi) — некоторое непустое подмножество множества значений переменной xi в обучающем наборе данных.
Механизм отсечения. Этим механизмом, имеющим название minimal cost-complexity tree pruning , алгоритм CART принципиально отличается от других алгоритмов конструирования деревьев решений. В рассматриваемом алгоритме отсечение — это некий компромисс между получением дерева «подходящего размера» и получением наиболее точной оценки классификации. Метод заключается в получении последовательности уменьшающихся деревьев, но деревья рассматриваются не все, а только «лучшие представители».
Перекрестная проверка (V- fold cross-validation) является наиболее сложной и одновременно оригинальной частью алгоритма CART . Она представляет собой путь выбора окончательного дерева, при условии, что набор данных имеет небольшой объем или же записи набора данных настолько специфические, что разделить набор на обучающую и тестовую выборку не представляется возможным.
Итак, основные характеристики алгоритма CART : бинарное расщепление, критерий расщепления — индекс Gini, алгоритмы minimal cost-complexity tree pruning и V- fold cross-validation, принцип «вырастить дерево, а затем сократить», высокая скорость построения, обработка пропущенных значений.
Алгоритм C4.5
Алгоритм C4.5 строит дерево решений с неограниченным количеством ветвей у узла. Данный алгоритм может работать только с дискретным зависимым атрибутом и поэтому может решать только задачи классификации. C4.5 считается одним из самых известных и широко используемых алгоритмов построения деревьев классификации.
Для работы алгоритма C4.5 необходимо соблюдение следующих требований:
- Каждая запись набора данных должна быть ассоциирована с одним из предопределенных классов, т.е. один из атрибутов набора данных должен являться меткой класса.
- Классы должны быть дискретными. Каждый пример должен однозначно относиться к одному из классов.
- Количество классов должно быть значительно меньше количества записей в исследуемом наборе данных.
Последняя версия алгоритма — алгоритм C4.8 — реализована в инструменте Weka как J4.8 (Java). Коммерческая реализация метода: C5.0, разработчик RuleQuest, Австралия.
Алгоритм C4.5 медленно работает на сверхбольших и зашумленных наборах данных.
Мы рассмотрели два известных алгоритма построения деревьев решений CART и C4.5. Оба алгоритма являются робастными, т.е. устойчивыми к шумам и выбросам данных.
Алгоритмы построения деревьев решений различаются следующими характеристиками:
- вид расщепления — бинарное (binary), множественное (multi-way)
- критерии расщепления — энтропия, Gini, другие
- возможность обработки пропущенных значений
- процедура сокращения ветвей или отсечения
- возможности извлечения правил из деревьев.
Ни один алгоритм построения дерева нельзя априори считать наилучшим или совершенным, подтверждение целесообразности использования конкретного алгоритма должно быть проверено и подтверждено экспериментом.
Разработка новых масштабируемых алгоритмов
Наиболее серьезное требование, которое сейчас предъявляется к алгоритмам конструирования деревьев решений — это масштабируемость, т.е. алгоритм должен обладать масштабируемым методом доступа к данным.
Разработан ряд новых масштабируемых алгоритмов, среди них — алгоритм Sprint, предложенный Джоном Шафером и его коллегами [36]. Sprint, являющийся масштабируемым вариантом рассмотренного в лекции алгоритма CART , предъявляет минимальные требования к объему оперативной памяти.
Выводы
В лекции мы рассмотрели метод деревьев решений; определить его кратко можно как иерархическое, гибкое средство предсказания принадлежности объектов к определенному классу или прогнозирования значений числовых переменных.
Качество работы рассмотренного метода деревьев решений зависит как от выбора алгоритма, так и от набора исследуемых данных. Несмотря на все преимущества данного метода, следует помнить, что для того, чтобы построить качественную модель, необходимо понимать природу взаимосвязи между зависимыми и независимыми переменными и подготовить достаточный набор данных.
Источник
Алгоритм CART (CART algorithm)
Популярный алгоритм построения деревьев решений, который может работать как с дискретной, так и с непрерывной выходной переменной, т.е. решать задачи и классификации, и регрессии.
Алгоритм строит бинарные деревья решений, которые содержат только два потомка в каждом узле. В процессе работы происходит рекурсивное разбиение примеров обучающего множества на подмножества, записи в которых имеют одинаковые значения целевой переменной.
Алгоритм реализует обучение с учителем и использует в качестве критерия для выбора разбиений в узлах индекс чистоты Джини (Gini impurity index). В процессе роста дерева алгоритм CART проводит для каждого узла полный перебор всех атрибутов, на основе которых может быть построено разбиение, и выбирает тот, который максимизирует значение индекса Джини.
Основная идея алгоритма заключается в том, чтобы выбрать такое разбиение из всех возможных в данном узле, чтобы полученные дочерние узлы были максимально однородными. При этом каждое разбиение производится только по одному атрибуту.
Если атрибут X , по которому производится разбиение, является номинальным c I категориями, то для него существует 2 ( I − 1 ) возможных разбиения, а если порядковым или непрерывным с K различными значениями, существует K − 1 различных разбиений по X . Дерево строится, начиная с корневого узла, путем итеративного использования следующих шагов в каждом узле:
- Для каждого атрибута ищется лучшее разбиение (в смысле однородности результирующих подмножеств).
- Среди всех разбиений, найденных на предыдущем шаге, выбирается то, для которого критерий разбиения наибольший.
- Узел разбивается с использованием лучшего разбиения, найденного на шаге 2, если не выполнено условие остановки.
Процедура упрощения деревьев решений, построенных на основе алгоритма CART, реализуется с помощью специального метода соотношения издержки-сложность (Cost-Complexity Pruning) и перекрестной проверки (для малых наборов данных, где полноценное разделение на обучающее и тестовое множества проблематично).
Алгоритм обладает следующими преимуществами:
- не является статистическим, поэтому не требует вычисления параметров вероятностных распределений;
- атрибуты разбиения выбираются непосредственно в процессе построения дерева, поэтому нет необходимости проводить процедуру отбора переменных для модели;
- устойчив к выбросам и аномальным значениям;
- высокая скорость работы.
К недостаткам алгоритма можно отнести неустойчивость относительно данных: даже небольшие изменения в обучающем множестве порождают значительные изменения в структуре дерева решений.
Алгоритм предложен в 1984 г. Лео Брейманом, Джеромом Фридманом, Ричардом Олшеном и Чарльзом Стоуном.
Источник
Решающие деревья в задачах регрессии. Алгоритм CART
На предыдущих занятиях мы с вами рассматривали решающие деревья для задач классификации. Однако, в ряде случаев, их применяют и для задач регрессии, когда алгоритм на выходе формирует одно вещественное значение (или несколько значений) для каждого входного вектора . То есть, в листьях такого дерева хранятся соответствующие вещественные числа.
Давайте, для определенности, я сразу приведу пример такого решающего дерева.
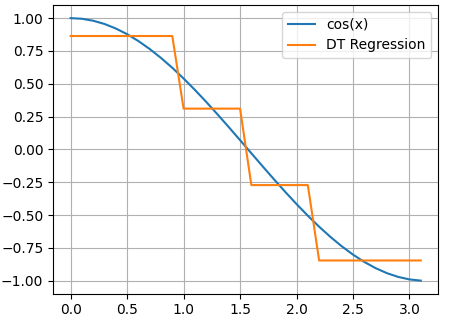
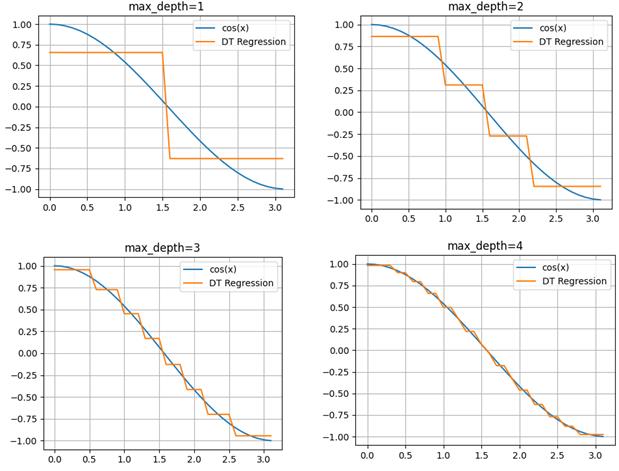
Смотрите, изначально наши данные представляют собой точки функции cos(x):
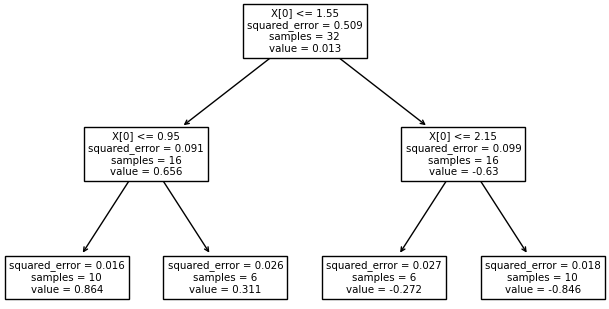
Здесь аргумент функции cos() – это признак, а значения функции в каждой точке – целевые переменные. Затем, по признаку (аргументу функции) выполняется разделение исходного множества точек на непересекающиеся подмножества. В результате, при глубине дерева два, получаем четыре подинтервала и четыре листа. Причем, в каждом листе хранится одно константное вещественное значение, которым заменяются все значения выделенного подмножества. Поэтому мы видим на графике ступенчатую функцию при аппроксимации косинусоиды решающим деревом.
Вот общая идея использования решающих деревьев для задач регрессии. И здесь возникают два главных вопроса:
- По какому критерию оценивать качество деления на подмножества (то есть, что использовать в качестве меры неопределенности – impurity)?
- Как вычислять вещественные значения в полученных листовых вершинах?
Хорошая новость, что на оба этих вопроса имеется единый ответ. Я начну с последнего. Часто в задачах регрессии требуется обеспечить минимум среднеквадратичной ошибки прогноза: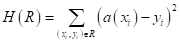 
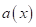
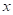
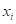
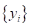
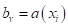
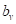
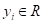
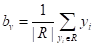
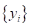
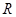
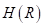
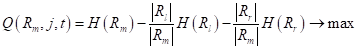
Здесь 
— ответ (прогноз) модели на входной вектор признаков ; 
— множество объектов 
, дошедших до некоторой листовой вершины v, и соответствующие им целевые значения 
. Так как при использовании решающих деревьев каждое подмножество аппроксимируется некоторым константным значением: 
то для минимизации квадратичного критерия, величину 
следует вычислять, как среднее арифметическое от всех целевых значений 
, попавших в листовую вершину v дерева: 
Можно легко доказать, что эта величина будет наилучшим образом описывать значения подмножества при квадратичном критерии. Так как величина 
зависит от множества , а значит, от способа разбиения деревом исходной обучающей выборки, то ее было бы логично использовать в качестве меры информативности (impurity) и выбирать в каждой промежуточной вершине разбиение так, чтобы максимизировался информационный выигрыш: 
То есть, мы будем выбирать порог t так, чтобы impurity левого и правого подмножеств 
были как можно меньше. Вот примеры разбиения исходной последовательности деревом глубиной от единицы до четырех: 
Как видите, вначале выделяются два равных подмножества и две константы, которые грубо описывают график косинусоиды. И это описание наилучшее с точки зрения квадратического критерия. При увеличении глубины, получаем все больше и больше информации об исходном сигнале, и для глубины 4 вполне угадывается график косинусоиды.
Реализация решающих деревьев на Python с помощью Scikit-Learn
Итак, мы с вами в целом познакомились с идеей решающих деревьев для задач классификации и регрессии. Осталось узнать, как можно реализовать эти подходы при решении практических задач. В самом простом варианте это можно сделать на языке Python с использованием библиотеки Scikit-Learn. В этой библиотеке имеется ветка:
которая отвечает за построение решающих деревьев. Разработчики Scikit-Learn использовали алгоритм: Classification and Regression Trees (CART) с помощью которого можно выполнять как классификацию, так и решать задачи регрессии. Подробнее об этом можно почитать на странице официальной документации: https://scikit-learn.org/stable/modules/tree.html Давайте, вначале построим решающее дерево для задачи регрессии. Для этого сформируем обучающее множество в виде значений функции косинуса:
import numpy as np import matplotlib.pyplot as plt x = np.arange(0, np.pi, 0.1).reshape(-1, 1) y = np.cos(x)
clf = tree.DecisionTreeRegressor(max_depth=3) clf = clf.fit(x, y)
Источник