Алгоритм для создания дерево

Алгоритм формирования бинарного дерева «в ширину»

3. Если прочитанный символ точка, то БД пустое, иначе создать корень, записать в него символ, корень поместить в очередь.

4. Пока очередь не пуста, выполнять п.5.

5. Взять вершину из очереди. Прочитать символ. Если символ точка, то левое поддерево пустое, иначе создать корень левого поддерева, записать в него символ и включить в очередь. Прочитать следующий символ. Если символ точка, то правое поддерево пустое, иначе создать корень правого поддерева, записать в него символ и включить в очередь.

При обходе БД (см. рис.25) в обратном порядке получим последовательность: ..D..EC..FB. I..JHGA

Если ограничить эту последовательность концевым маркером, то ее можно будет использовать в качестве исходных данных для формирования БД «снизу вверх».

Алгоритм формирования бинарного дерева «снизу вверх»

1. Инициализировать очередь.

2. Последовательно обрабатывать символы последовательности, пока не достигнут концевой маркер.

3. Если прочитанный символ точка, то поместить в очередь пустое БД, иначе создать корень, записать в него символ, взять из очереди его левое, затем правое поддерево, полученное БД поместить в очередь.

4. Если по окончании работы алгоритма очередь окажется пустой, то сформировано пустое БД, иначе очередь будет содержать единственный элемент — корень сформированного дерева.

При обходе БД (см. рис.25) в симметричном порядке получим последовательность: .D.C.E.B.F.A.G.I.H.J.

Такую же последовательность получим при обходе в симметричном порядке БД на рис.26, поэтому она неоднозначно определяет БД и не может быть использована в качестве исходных данных для формирования БД.

Рассмотрим алгоритм формирования БД, в котором для любой вершины T_i значения всех вершин в левом поддереве должны быть меньше значения в вершине T_i, а в правом — больше. Такое дерево можно построить, обработав последовательность неповторяющихся значений.

Рекурсивный алгоритм формирования бинарного дерева

1. Прочитать элемент последовательности.

2. Если БД пустое, то создать корень и записать в него значение элемента, иначе включить элемент в левое поддерево, если его значение меньше значения корня, или включить в правое поддерево, если значение элемента больше значения корня.

Итеративный алгоритм формирования бинарного дерева

1. Пока в последовательности неповторяющихся значений есть элементы, читать и включать их в дерево в соответствии с п.2 или п.3.

2. Если БД пустое, то создать корень, записать в него значение.

3. Если значение элемента меньше значения корня и у корня есть левый сын, то перейти к левому сыну, считать его корнем и выполнять п.3, если же левого сына нет, то создать и записать в него значение элемента. Если значение элемента больше значения корня и у корня есть правый сын, то перейти к правому сыну, считать его корнем и выполнять п.3, если же правого сына нет, то создать и записать в него значение элемента.

Применив рассмотренные алгоритмы к последовательности целых чисел 20, 15, 23, 10, 5, 12, 30, 18, 44, 25 получим БД на рис.27.

Рис.27. БД, построенное по итеративному алгоритму

Если последовательность будет упорядоченной, то БД вырождается в последовательность.

Пусть необходимо построить БД для последовательности из n элементов, имеющее минимальную высоту. Тогда все уровни дерева, кроме, может быть, последнего, будут заполнены. Для того чтобы построить такое БД, нужно элементы последовательности распределять поровну между левым и правым поддеревом. Такое распределение достаточно просто можно выполнить для упорядоченной по возрастанию последовательности.

Источник

Создание бинарного дерева

Когда я начал изучать ruby, я решил реализовать бинарное дерево и некоторые из его основных операций (insert, delete, walk, и search), для того, что бы лучше вникнуть в язык. Бинарные деревья, это хорошее упражнение, что бы понять особенности языка, такие как: условные операторы, циклы, классы. В то же время, это возможность решить интересную задачу. Алгоритм бинарного дерева хорошо описан во многих книгах и в интернете.
Для усложнения задачи, я так же реализовал отрисовку бинарного дерева средствами html5 и Canvas. Это позволяет более наглядно понять работу бинарного дерева. Вы можете посмотреть демонстрацию на веб сайте.
Далее я кратко опишу реализацию основных методов построения бинарного дерева.

Бинарное дерево или дерево двоичного поиска

Собственно код, представленный ниже, реализует Дерево двоичного поиска (BST), которое является более конкретной версией бинарных деревьев. В двоичном дереве, каждый узел имеет не более 2 детей, один из них называется «левое поддерево», а другой «правое поддерево», сортировка отсутствует. В двоичном дереве поиска, все узлы хранятся в порядке, отраженном в следующем правиле:

Допустим x это узел в двоичном дереве поиска, если y является «левым поддеревом» для x, то y.key ≤ x.key. Если y является «правым поддеревом» для x, то y.key ≥ x.key.

Реализация бинарного дерева поиска

Класс, для работы с деревом, который я реализовал можно использовать следующим образом:

require "binarytree" tree = BinaryTree.new(40) tree.add(30) tree.add(100) tree.add(20) tree.add(35) tree.add(25) tree.add(34) puts "Tree nodes: #" => "20, 25, 30, 34, 35, 40, 100"

Этот клас мы можем использовать с числами, строками или любыми собственными типами ruby, поддерживающими сопоставление (т.е. )

Добавление узлов в бинарном дереве

Код для добавления узлов в бинарном дереве показан ниже. Этот код сначала проверяет, есть ли у нас уже корневой узел, если нет, то создаем корневой узел с новым значением. Если у нас уже есть корневой узел, сканируем узлы дерева (с помощью правила указанного выше) пока не дойдем до конечного узла. Как только мы достигли конечного узла мы обновляем его, чтобы указать на новый узел.

 def add(new_value) if @root == nil @root = Node.new(new_value) @total_nodes = 1 return end current = @root while(true) if new_value >= current.value if current.right == nil current.right = Node.new(new_value) break else current = current.right end else if current.left == nil current.left = Node.new(new_value) break else current = current.left end end end @total_nodes += 1 end 

Ходьба по дереву

Одним из преимуществ двоичного дерева поиска в том, что очень легко получить значения, хранящиеся в нем. Этот процесс называется «ходьба по отсортированному дереву». Например, если у нас есть дерево со следующими значениями: 100, 50, 200 и 150, то отсортированное дерево даст нам значения: 50, 100, 150 и 200. Хождение по дереву можно реализовать с помощью рекурсивной функции. Однако рекурсивный метод, хотя и элегантный, но не очень эффективен, если дерево большого размера. Код, который я реализовал не использует рекурсию, но вместо этого использует массив, как стек для отслеживания узлов, которые он посещает. Это решение не такое элегантное, как рекурсия, но оно хорошо работает, даже если в дереве тысячи узлов.

 def walk return nil if @root == nil node = @root stack = [] ignore_left = false while(true) #p "processing #" if ignore_left #p "ignoring nodes to the left" ignore_left = false else if node.left != nil #p "moving to the left" stack  

 def draw_node(root, x, y, block) return if root == nil block.call(root, x, y, x, y) draw_left(root.left, x, y, block) if root.left != nil draw_right(root.right, x, y, block) if root.right != nil end 

 def draw_left(node, parent_x, parent_y, block) if node.right != nil count = 1 + children_count(node.right) else count = 0 end x = parent_x - @x_distance - (count*@x_distance) y = parent_y + @y_distance block.call(node.value, x, y, parent_x, parent_y) draw_left(node.left, x, y, block) if node.left != nil draw_right(node.right, x, y, block) if node.right != nil end 

 def draw_right(node, parent_x, parent_y, block) if node.left != nil count = 1 + children_count(node.left) else count = 0 end x = parent_x + @x_distance + (count*@x_distance) y = parent_y + @y_distance block.call(node.value,x,y, parent_x, parent_y) draw_left(node.left, x, y, block) if node.left != nil draw_right(node.right, x, y, block) if node.right != nil end 

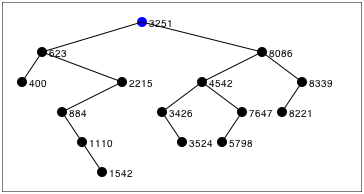
 require "binarytree" require "binarytreedrawer" tree = BinaryTree.new tree.add(100) tree.add(50) tree.add(150) tree.add(25) tree.add(75) tree.add(125) tree.add(175) drawer = BinaryTreeDrawer.new(tree) drawer.draw(0,0, Proc.new < |value, x, y, px, py| puts "Value #at (#, #)" >) => Value 100 at (0, 0) => Value 50 at (-40, 30) => Value 25 at (-60, 60) => Value 75 at (-20, 60) => Value 150 at (40, 30) => Value 125 at (20, 60) => Value 175 at (60, 60) 

 drawer = BinaryTreeDrawer.new(@tree) drawer.draw(0, 0, Proc.new < |value, x, y, px, py| circles , offsetY + #, 5);" lines , offsetY + #, centerX + #, offsetY + #);" labels , offsetY+5+#, \"#\");" >)