Алгоритм нахождения пути дерева

Алгоритмы на деревьях

Пусть дан граф [math]G = \langle V, E \rangle [/math] . Тогда диаметром [math]d[/math] называется [math]\max\limits_ dist(v, u)[/math] , где [math]dist[/math] — кратчайшее расстояние между вершинами.

Алгоритм

• Возьмём любую вершину [math] v \in V [/math] и найдём расстояния до всех других вершин. [math]d[i] = dist(v, i)[/math]

• Возьмём вершину [math] u \in V [/math] такую, что [math]d[u] \geqslant d[t][/math] для любого [math]t[/math] . Снова найдём расстояние от [math]u[/math] до всех остальных вершин. Самое большое расстояние — диаметр дерева.

Расстояние до остальных вершин будем искать алгоритмом [math]BFS[/math] .

Реализация

//граф g представлен списком смежности int diameterTree(list> g): v = u = w = 0 d = bfs(g, v) for i = 0, i < n, i++ if d[i] > d[u] u = i d = bfs(g, u) for i = 0, i < n, i++ if d[i] > d[w] w = i return d[w]

Обоснование корректности

Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.

После запуска алгоритма получим дерево [math]BFS[/math] .

В дереве [math]BFS[/math] не существует ребер между вершинами из разных поддеревьев некоторого их общего предка.

Предположим, существует ребро [math]u, v[/math] между соседними поддеревьями:

Мы свели задачу к нахождению вершины [math]w[/math] , такой что сумма глубин поддеревьев максимальна.

Докажем, что одно из искомых поддеревьев содержит самый глубокий лист. Пусть нет, тогда, взяв расстояние от [math]w[/math] до глубочайшего листа, мы можем улучшить ответ.

Таким образом мы доказали, что нам нужно взять вершину [math]u[/math] с наибольшей глубиной после первого [math]BFS[/math] , очевидно, что ей в пару надо сопоставить вершину [math]w[/math] , такую что [math]dist(u, w)[/math] максимально. Вершину [math]w[/math] можно найти запуском [math]BFS[/math] из [math]u[/math] .

Оценка времени работы

Все операции кроме [math]BFS[/math] — [math]O(1)[/math] . [math]BFS[/math] работает за линейное время, запускаем мы его два раза. Получаем [math]O(|V| + |E|)[/math] .

Центр дерева

Определения

Определение:

Эксцентриситет вершины [math]e(v)[/math] (англ. eccentricity of a vertex) — [math]\max\limits_ dist(v, u)[/math] , где [math]V[/math] — множество вершин связного графа [math]G[/math] .

Определение:

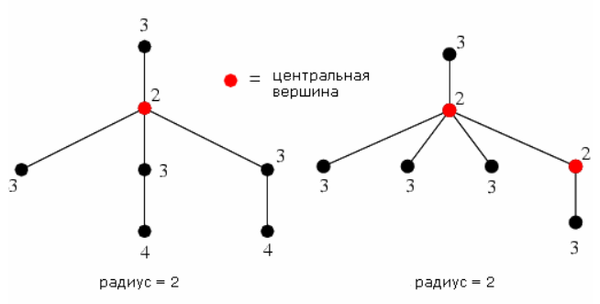
Радиус [math]r(G)[/math] (англ. radius) — наименьший из эксцентриситетов вершин графа [math]G[/math] .

Определение:

Центральная вершина (англ. central vertex) — вершина графа [math]G[/math] , такая что [math]e(v) = r(G)[/math]

Определение:

Центр графа [math]G[/math] (англ. center of a graph) — множество всех центральных вершин графа [math]G[/math] .

Алгоритм

Наивный алгоритм

Найдём центр графа исходя из его определения.

• Построим матрицу [math]A_[/math] ( [math]n[/math] — мощность множества [math]V[/math] ), где [math]a_ = d_[/math] , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
• Подсчитаем максимум в каждой строчке матрицы [math]A[/math] . Таким образом, получим массив длины [math]n[/math] .
• Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.

Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет [math]O(V^3)[/math] , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и [math]O(V^2)[/math] , за которую мы находим максимумы в матрице.

Алгоритм для дерева за O(n)

Собственно, алгоритм нахождения центра описан в доказательстве теоремы.

• Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом [math]0[/math] .
• Обрежем помеченные вершины.
• Образовавшиеся листья пометим числом [math]1[/math] и тоже обрежем.
• Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.

Оставшиеся листья являются центром дерева.

Для того, чтобы алгоритм работал за [math]O(n)[/math] , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.

См. также

Источники информации

Источник

Найдите путь максимальной суммы между двумя листьями в бинарном дереве.

Для заданного бинарного дерева напишите эффективный алгоритм нахождения максимальной суммы пути между любыми двумя его листьями. Предположим, что бинарное дерево не асимметрично и содержит не менее двух узлов.

Например, максимальный суммарный путь в следующем бинарном дереве равен 22:

Простым решением было бы вычислить максимальную сумму пути от узла к листу от левого и правого дочерних элементов для каждого узла в дереве. Максимальный суммарный путь между двумя листьями, который проходит через узел, имеет значение, равное максимальной сумме пути от узла к листу его левого и правого дочерних элементов плюс значение узла. Наконец, рассмотрим максимальное значение среди всех путей с максимальной суммой, найденных для каждого узла в дереве.

Временная сложность этого решения O(n 2 ) как есть n узлов в дереве, и для каждого узла мы вычисляем максимальную сумму пути от узла к листу его левого и правого поддерева, который занимает O(n) время.

Мы можем решить эту задачу за линейное время, обходя дерево снизу вверх. Вместо вычисления максимального суммарного пути от узла к листу левого и правого дочерних элементов для каждого узла в дереве вычислите максимальный суммарный путь между двумя листьями, который проходит через узел за постоянное время. Идея состоит в том, чтобы начать с нижней части дерева и вернуть максимальную сумму пути от узла к листу для каждого узла до его родителя.

Алгоритм может быть реализован следующим образом на C++, Java и Python. Здесь мы передаем путь максимальной суммы по ссылке на функцию (вместо того, чтобы возвращать ее) и обновляем его значение внутри самой функции, используя возвращаемое значение левого и правого поддеревьев.

Источник

Вывести все пути от корня до листовых узлов бинарного дерева

Для заданного бинарного дерева напишите эффективный алгоритм для вывода всех путей от корневого узла до каждого конечного узла в нем.

Например, рассмотрим следующее бинарное дерево:

The binary tree has four root-to-leaf paths:

1 —> 2 —> 4
1 —> 2 —> 5
1 —> 3 —> 6 —> 8
1 —> 3 —> 7 —> 9

Идея состоит в том, чтобы обойти дерево в предзаказ моды и сохранить каждый встреченный узел на текущем пути от корня к листу в векторе. Если мы встретим листовой узел, выведите все узлы, присутствующие в векторе. Ниже приведена реализация этой идеи на C++, Java и Python:

C++

результат:

1 2 4
1 2 5
1 3 6 8
1 3 7 9

Java

результат:

[1, 2, 4]
[1, 2, 5]
[1, 3, 6, 8]
[1, 3, 7, 9]

Python

результат:

[1, 2, 4]
[1, 2, 5]
[1, 3, 6, 8]
[1, 3, 7, 9]

Временная сложность приведенного выше решения равна O(n) , куда n это общее количество узлов в бинарном дереве. Программа требует O(h) дополнительное место для стека вызовов, где h это высота дерева.

Проблема кажется немного сложной для решения без рекурсии. Существует один обходной путь, когда мы сохраняем путь от корня к листу в строке, когда мы итеративно проходим по дереву, и печатаем путь всякий раз, когда встречаем какой-либо конечный узел. Это показано ниже на C++, Java и Python:

Источник