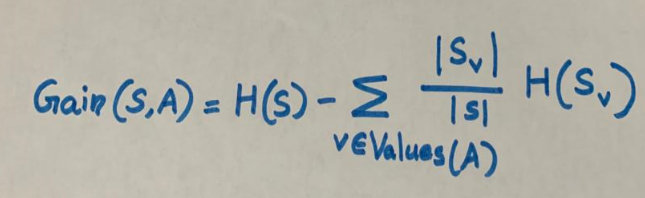Алгоритм построения дерева принятия решений

Деревья решений и алгоритмы их построения

Сегодня мы поговорим об одном из классических методов интеллектуального анализа данных (англ. data mining) – построении деревьев решений, расскажем о его основных принципах и подробнее остановимся на алгоритмах его реализации.

Что такое дерево принятия решений?

Согласно наиболее общему определению, дерево принятия решений – это средство поддержки принятия решений при прогнозировании, широко применяющееся в статистике и анализе данных. Нас с вами больше интересует второй вариант использования, однако прежде чем перейти к вопросам о пользе деревьев решений для мира больших данных и конкретным алгоритмам, хотелось бы упомянуть о важнейших понятиях, связанных с методом в целом.

Итак, дерево решений, подобно его «прототипу» из живой природы, состоит из «ветвей» и «листьев». Ветви (ребра графа) хранят в себе значения атрибутов, от которых зависит целевая функция; на листьях же записывается значение целевой функции. Существуют также и другие узлы – родительские и потомки – по которым происходит разветвление, и можно различить случаи.

Пример использования

Цель всего процесса построения дерева принятия решений – создать модель, по которой можно было бы классифицировать случаи и решать, какие значения может принимать целевая функция, имея на входе несколько переменных.

Как пример, представим случай, когда необходимо принять решение о выдаче кредита (целевая функция может принимать значения «да» и «нет») на основе информации о клиенте (несколько переменных: возраст, семейное положение, уровень дохода и так далее). К примеру, переменная «возраст» с атрибутом «менее 21 одного года = да» сразу приведет от корневого узла дерева к его листу, причем целевая функция «выдача кредита» примет значение «нет». Если возраст составляет более 21 года, то ветвь приведет нас к очередному узлу, который, к примеру, «спросит» нас об уровне дохода клиента. Таким образом, классификация каждого нового случая происходит при движении вниз до листа, который и укажет нам значение целевой функции в каждом конкретном случае.

Общий алгоритм построения дерева принятия решения

Предлагаем рассмотреть на нашем примере общий алгоритм построения дерева, чтобы затем перейти к его частным случаям:

• Вначале необходимо выбрать атрибут Q (в нашем случае, допустим: уровень дохода > 500$ в месяц) и поместить его в корневой узел.
• Затем, из наших тестовых примеров (или набора данных) для каждого значения атрибута i (в нашем случае их два – «да» и «нет») выбираем только те, для которых Q=i.
• Далее, рекурсивно строим дерево принятия решений.

Основная проблема, очевидно, кроется в первом шаге – на каком основании выбирается каждый следующий атрибут Q? На этот вопрос существует несколько ответов в виде частных алгоритмов принятия решений – главными из которых являются алгоритмы ID3, C4.5 и CART

Основные частные алгоритмы

1. ID3. В основе этого алгоритма лежит понятие информационной энтропии – то есть, меры неопределенности информации (обратной мере информационной полезности величины). Для того чтобы определить следующий атрибут, необходимо подсчитать энтропию всех неиспользованных признаков относительно тестовых образцов и выбрать тот, для которого энтропия минимальна. Этот атрибут и будет считаться наиболее целесообразным признаком классификации.
2. C5. Этот алгоритм – усовершенствование предыдущего метода, позволяющее, в частности, «усекать» ветви дерева, если оно слишком сильно «разрастается», а также работать не только с атрибутами-категориями, но и с числовыми. В общем-то, сам алгоритм выполняется по тому же принципу, что и его предшественник; отличие состоит в возможности разбиения области значений независимой числовой переменной на несколько интервалов, каждый из которых будет являться атрибутом. В соответствии с этим исходное множество делится на подмножества. В конечном итоге, если дерево получается слишком большим, возможна обратная группировка – нескольких узлов в один лист. При этом, поскольку перед построением дерева ошибка классификации уже учтена, она не увеличивается.
3. CART. Алгоритм разработан в целях построения так называемых бинарных деревьев решений – то есть тех деревьев, каждый узел которых при разбиении «дает» только двух потомков. Грубо говоря, алгоритм действует путем разделения на каждом шаге множества примеров ровно напополам – по одной ветви идут те примеры, в которых правило выполняется (правый потомок), по другой – те, в которых правило не выполняется (левый потомок). Таким образом, в процессе «роста» на каждом узле дерева алгоритм проводит перебор всех атрибутов, и выбирает для следующего разбиения тот, который максимизирует значение показателя, вычисляемого по математической формуле и зависящего от отношений числа примеров в правом и левом потомке к общему числу примеров.

Резюме

Деревья принятий решений – один из основных и наиболее популярных методов помощи в принятии решений. Действительно, построение деревьев решений позволяет наглядно продемонстрировать другим и разобраться самому в структуре данных, создать работающую модель классификации данных, какими бы «большими» они ни были.

Источник

Как разобраться в дереве принятия решений и сделать его на Python

Совсем скоро, 20 ноября, у нас стартует новый поток «Математика и Machine Learning для Data Science», и в преддверии этого мы делимся с вами полезным переводом с подробным, иллюстрированным объяснением дерева решений, разъяснением энтропии дерева решений с формулами и простыми примерами, вводом понятия «информационный выигрыш», которое игнорируется большинством умозрительно-простых туториалов. Статья рассчитана на любящих математику новичков, которые хотят больше разобраться в работе дерева принятия решений. Для полной ясности взят совсем маленький набор данных. В конце статьи — ссылка на код на Github.

Дерево решений — тип контролируемого машинного обучения, который в основном используется в задачах классификации. Дерево решений само по себе — это в основном жадное, нисходящее, рекурсивное разбиение. «Жадное», потому что на каждом шагу выбирается лучшее разбиение. «Сверху вниз» — потому что мы начинаем с корневого узла, который содержит все записи, а затем делается разбиение.

Корневой узел — самый верхний узел в дереве решений называется корневой узел.
Узел принятия решения — подузел, который разделяется на дополнительные подузлы, известен как узел принятия решения.

Лист/терминальный узел — узел, который не разделяется на другие узлы, называется терминальный узел, или лист.

Набор данных

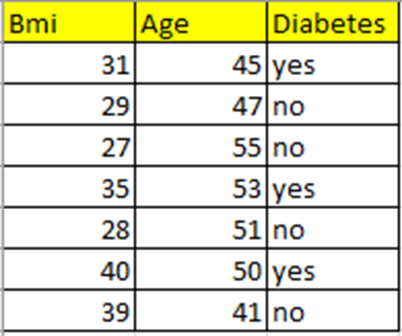
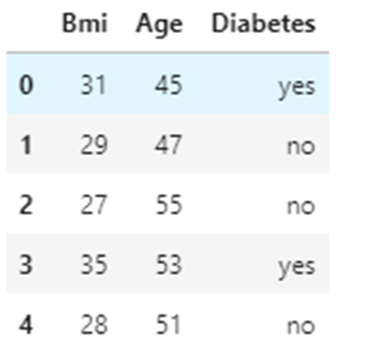
Я взяла совсем маленький набор данных, содержащий индекс массы тела (BMI), возраст (Age) и целевую переменную Diabetes (диабет). Давайте спрогнозируем, будет у человека данного возраста и индекса массы тела диабет или нет.

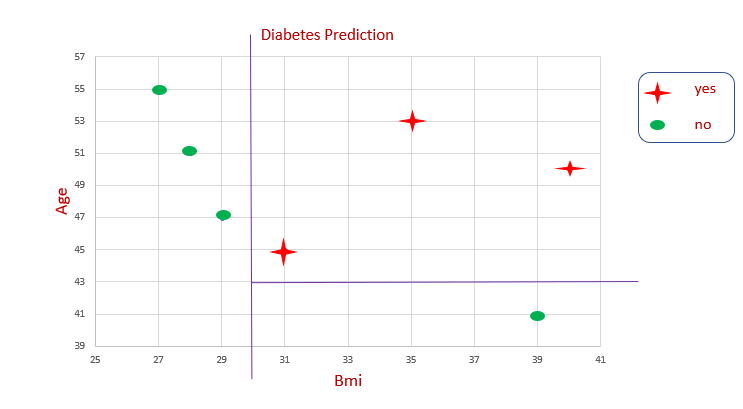
Представление набора данных

На графике невозможно провести какую-то прямую, чтобы определить границу принятия решения. Снова и снова мы разделяем данные, чтобы получить границу решения. Так работает алгоритм дерева решений.

Вот так в дереве решений происходит разбиение.

Важные теоретические определения

Энтропия

Энтропия — это мера случайности или неопределенности. Уровень энтропии колеблется от 0 до 1 . Когда энтропия равна 0, это означает, что подмножество чистое, то есть в нем нет случайных элементов. Когда энтропия равна 1, это означает высокую степень случайности. Энтропия обозначается символами H(S).

Формула энтропии

Энтропия вычисляется так: -(p(0) * log(P(0)) + p(1) * log(P(1)))

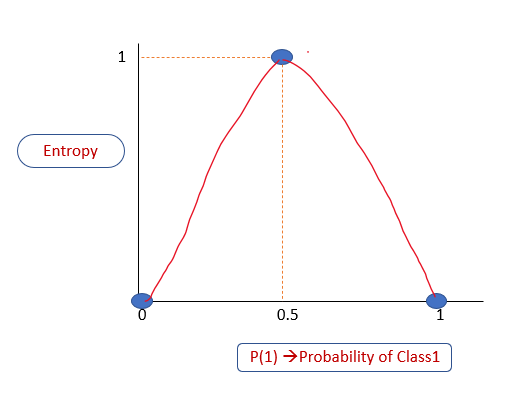
Связь между энтропией и вероятностью

Когда энтропия равна 0, это означает, что подмножество «чистое», то есть в нем нет энтропии: либо все «да», либо все голоса «нет». Когда она равна 1, то это означает высокую степень случайности. Построим график вероятности P(1) вероятности принадлежности к классу 1 в зависимости от энтропии. Из объяснения выше мы знаем, что:

Если P(1) равно 0, то энтропия равна 0
Если P(1) равно 1, то энтропия равна 0
Если P(1) равно 0,5, то энтропия равна 1

Уровень энтропии всегда находится в диапазоне от 0 до 1.

Информационный выигрыш

Информационный выигрыш для разбиения рассчитывается путем вычитания взвешенных энтропий каждой ветви из исходной энтропии. Используем его для принятия решения о порядке расположения атрибутов в узлах дерева решений.

Как работает дерево решений

В нашем наборе данных два атрибута, BMI и Age. В базе данных семь записей. Построим дерево решений для нашего набора данных.

1. Корневой узел

В дереве решений начнем с корневого узла. Возьмем все записи (в нашем наборе данных их семь) в качестве обучающих выборок.

В корневом узле наблюдаем три голоса за и четыре против.
Вероятность принадлежности к классу 0 равна 4/7. Четыре из семи записей принадлежат к классу 0.
P(0) = 4/7
Вероятность принадлежности к классу 1 равна 3/7. То есть три из семи записей принадлежат классу 1.
P(1) = 3/7.

Вычисляем энтропию корневого узла:

2. Как происходит разбиение?

У нас есть два атрибута — BMI и Age. Как на основе этих атрибутов происходит разбиение? Как проверить эффективность разбиения?

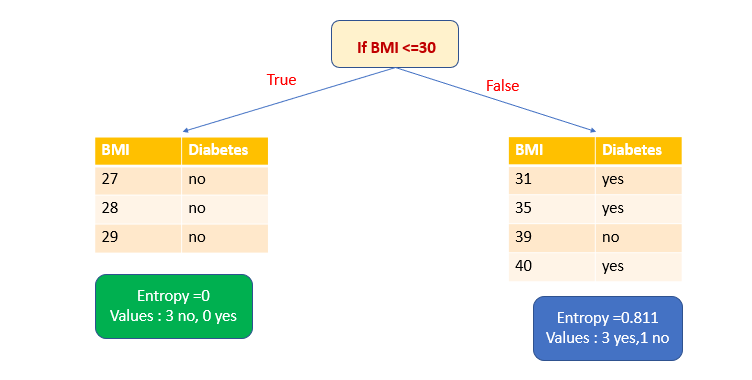
1. При выборе атрибута BMI в качестве переменной разделения и ≤30 в качестве точки разделения мы получим одно чистое подмножество.

Точки разбиения рассматриваются для каждой точки набора данных. Таким образом, если точки данных уникальны, то для n точек данных будет n-1 точек разбиения. То есть в зависимости от выбранных точки и переменной разбиения мы получаем высокий информационный выигрыш и выбираем разделение с этим выигрышем. В большом наборе данных принято считать только точки разделения при определенных процентах распределения значений: 10, 20, 30%. У нас набор данных небольшой, поэтому, видя все точки разделения данных, я выбрала в качестве точки разделения значения ≤30.

Энтропия чистого подмножества равна нулю. Теперь рассчитаем энтропию другого подмножества. Здесь у нас три голоса за и один против.

Чтобы решить, какой атрибут выбрать для разбиения, нужно вычислить информационный выигрыш.

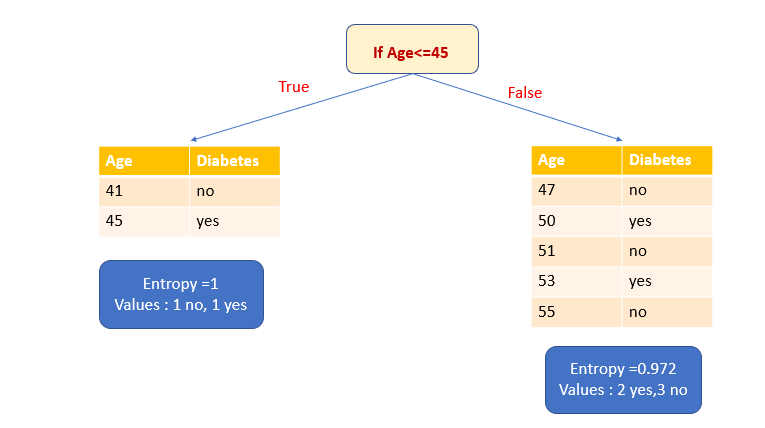
2. Выберем атрибут Age в качестве переменной разбиения и ≤45 в качестве точки разбиения.

Давайте сначала вычислим энтропию подмножества True. У него есть одно да и одно нет. Это высокий уровень неопределенности. Энтропия равна 1. Теперь рассчитаем энтропию подмножества False. В нем два голоса за и три против.

3. Рассчитаем информационный выигрыш.

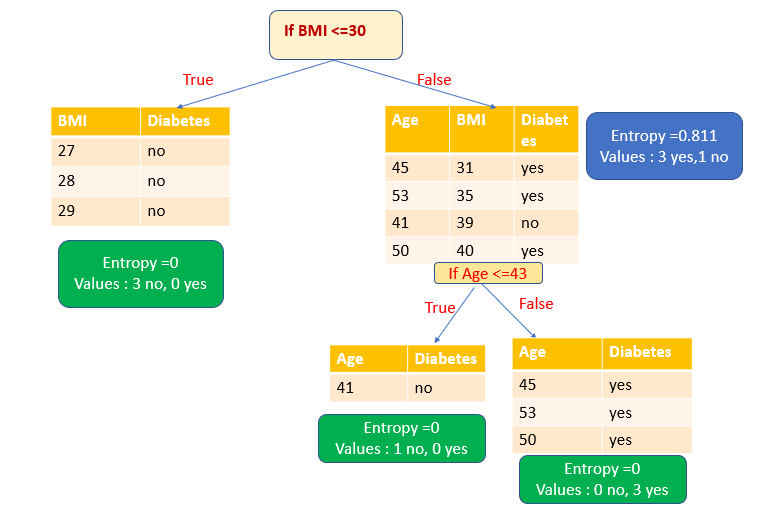
Мы должны выбрать атрибут, имеющий высокий информационный выигрыш. В нашем примере такую ценность имеет только атрибут BMI. Таким образом, атрибут BMI выбирается в качестве переменной разбиения. После разбиения по атрибуту BMI мы получаем одно чистое подмножество (листовой узел) и одно нечистое подмножество. Снова разделим это нечистое подмножество на основе атрибута Age. Теперь у нас есть два чистых подмножества (листовой узел).

Итак, мы создали дерево решений с чистыми подмножествами.

Напишем это на Python с помощью sklearn

1. Импортируем библиотеки.

import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns 

2. Загрузим данные.

df=pd.read_csv("Diabetes1.csv") df.head() 

3. Разделим переменные на x и y.

Атрибуты BMI и Age принимаются за x.
Атрибут Diabetes (целевая переменная) принимается за y.

x=df.iloc[. 2] y=df.iloc[:,2:] x.head(3) 

4. Построим модель с помощью sklearn

from sklearn import tree model=tree.DecisionTreeClassifier(criterion="entropy") model.fit(x,y) 

Вывод: DecisionTreeClassifier (criterion=«entropy»)

5. Оценка модели

Вывод: 1.0 . Мы взяли очень маленький набор данных, поэтому оценка равна 1.

6. Прогнозирование с помощью модели

Давайте предскажем, будет ли диабет у человека 47 лет с ИМТ 29. Напомню, что эти данные есть в нашем наборе данных.

Вывод: array([‘no’], dtype=object)
Прогноз — нет, такой же, как и в наборе данных. Теперь спрогнозируем, будет ли диабет у человека 47 лет с индексом массы тела 45. Отмечу, что этих данных в нашем наборе нет.

Вывод: array([‘yes’], dtype=object)

7. Визуализация модели:

Код и набор данных из этой статьи доступны на GitHub.

Приходите изучать математику к нам на курс «Математика и Machine Learning для Data Science» а промокод HABR, добавит 10 % к скидке на баннере.

Рекомендуемые статьи

Источник