Алгоритмы построения дерева кратчайших путей: от простых до сложных
Дерево кратчайших путей – это граф, который представляет собой подмножество вершин исходного графа, соединенных между собой ребрами с минимальными весами. Алгоритмы построения таких деревьев являются одними из фундаментальных задач графовой теории и находят множество применений в различных областях, включая транспортную логистику и маршрутизацию сетей.
Алгоритм Дейкстры
Алгоритм Дейкстры – это один из наиболее распространенных и известных алгоритмов построения дерева кратчайших путей. Он был разработан нидерландским ученым Эдсгером Дейкстрой в 1959 году и представляет собой жадный алгоритм, который работает только с неотрицательными весами ребер.
Описание алгоритма
Алгоритм Дейкстры начинает работу с одной стартовой вершины и последовательно просматривает все вершины графа, обновляя значения кратчайших расстояний до каждой из вершин. На каждом шаге алгоритма выбирается вершина с наименьшим расстоянием от стартовой вершины, после чего обновляются расстояния до всех вершин, смежных с выбранной. Повторив этот процесс для всех вершин графа, можно построить дерево кратчайших путей.
Пример
Рассмотрим граф, изображенный на рисунке:
И попробуем применить алгоритм Дейкстры для построения дерева кратчайших путей, начиная с вершины A.
- Помечаем вершину A и устанавливаем ее расстояние до себя равным 0.
- Рассчитываем расстояния до смежных вершин: B – 3, C – 2 и D – 6.
- Выбираем вершину C с наименьшим расстоянием и помечаем ее.
- Рассчитываем расстояния до смежных вершин: A – 2, B – 1 и E – 4.
- Выбираем вершину B с наименьшим расстоянием и помечаем ее.
- Рассчитываем расстояния до смежных вершин: A – 3, C – 1, D – 3 и E – 5.
- Выбираем вершину D с наименьшим расстоянием и помечаем ее.
- Рассчитываем расстояния до смежных вершин: A – 6, B – 3 и E – 6.
- Выбираем вершину E с наименьшим расстоянием и помечаем ее.
- Рассчитываем расстояния до смежных вершин: C – 4, B – 5 и D – 6.
- Все вершины помечены, построение дерева кратчайших путей завершено. Результат можно увидеть на рисунке:
Алгоритм Беллмана-Форда
Алгоритм Беллмана-Форда также является широко используемым алгоритмом для построения дерева кратчайших путей. Он был разработан двумя учеными – Ричардом Беллманом и Лестером Фордом – в 1958 году и подходит для графов с отрицательными весами ребер.
Описание алгоритма
Алгоритм Беллмана-Форда работает итеративно и на каждой итерации обновляет значения расстояний до каждой вершины графа. На первой итерации расстояние до стартовой вершины устанавливается равным 0, а до всех остальных вершин – бесконечности. Далее на каждой следующей итерации алгоритма обновляются расстояния до всех вершин, смежных с обрабатываемой.
Если на n-ой итерации произошли обновления расстояний, то в графе есть цикл отрицательного веса, и алгоритм завершается с ошибкой. В противном случае построение дерева кратчайших путей завершается.
Пример
Рассмотрим граф с отрицательными весами ребер, изображенный на рисунке:
И попробуем применить алгоритм Беллмана-Форда для построения дерева кратчайших путей, начиная с вершины A.
- Устанавливаем расстояние до вершины A равным 0, а до всех остальных вершин – бесконечности.
- Рассчитываем расстояния до смежных вершин: B – 5 и C – 8.
- Рассчитываем расстояния до смежных вершин: B – 2, C – 5 и D – 4.
- Рассчитываем расстояния до смежных вершин: B – 2, C – 5 и E – 7.
- Рассчитываем расстояния до смежных вершин: C – 2, D – 1 и E – 4.
- Рассчитываем расстояния до смежных вершин: E – 2.
- Все вершины помечены, построение дерева кратчайших путей завершено. Результат можно увидеть на рисунке:
Алгоритм Флойда-Уоршелла
Алгоритм Флойда-Уоршелла является алгоритмом динамического программирования, который позволяет решить задачу о кратчайших путях между всеми парами вершин графа. Он был разработан Робертом Флойдом и Стивеном Уоршеллом в 1962 году.
Описание алгоритма
Алгоритм Флойда-Уоршелла работает в несколько этапов. На каждом этапе алгоритма рассчитывается матрица расстояний между всеми парами вершин, учитывая только промежуточные вершины в пределах определенного диапазона номеров.
На первом этапе диапазон номеров промежуточных вершин состоит только из стартовых вершин, на втором – из стартовых вершин и вершин, номера которых не превышают 1, на третьем – из всех вершин.
Пример
Рассмотрим граф, изображенный на рисунке:
И попробуем применить алгоритм Флойда-Уоршелла для построения матрицы расстояний между всеми парами вершин.
Таким образом, мы получаем матрицу расстояний между всеми парами вершин. Если требуется построить дерево кратчайших путей для каждой вершины графа, то можно использовать полученную матрицу и применить алгоритм, описанный выше для каждой стартовой вершины.
Заключение
Алгоритмы построения дерева кратчайших путей представляют собой одну из фундаментальных задач графовой теории. Каждый алгоритм имеет свои особенности и подходит для решения определенных типов задач. Некоторые из них могут работать только с неотрицательными весами ребер, другие – с отрицательными. В зависимости от поставленной задачи можно выбрать подходящий алгоритм или же комбинировать их для достижения оптимального результата.
Источник
Три алгоритма на графах
Пусть G=(V,E) — ориентированный граф , для каждого ребра 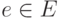
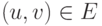 (если
(если  , то считаем, что
, то считаем, что 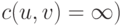 и исходная вершина
и исходная вершина 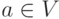 .
.