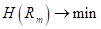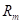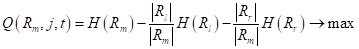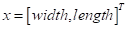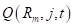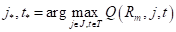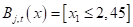29.Алгоритм id3 построения дерева решений
Алгоритм ID3 (iterative dichotomizer 3) один из простейших и популярных алгоритмов. Рассмотрим его на примере, заимствованном из [1].
Алгоритм начинает работу со всеми обучающими примерами в корневом узле дерева. Для разделения множества примеров корневого узла выбирается один из атрибутов, и для каждого значения, принимаемого этим атрибутом, строится ветвь и создается дочерний узел. Затем все примеры распределяются по дочерним узлам в соответствии со значением атрибута. Например, атрибут принимает три значения: . Тогда при разбиении исходного множества по атрибуту алгоритм создаст три дочерних узла, в первый из которых будут помещены все записи со значением , во второй – со значением , а в третий – со значением .
Алгоритм повторяется рекурсивно до тех пор, пока в узлах не останутся только примеры одного класса, после чего узлы будут объявлены листами и разбиение прекратится. Наиболее сложным этапом алгоритма является выбор атрибута, по которому будет производиться разбиение в каждом узле. Для выбора атрибута разбиения ID3 использует критерий, называемый приростом информации (information gain), или уменьшением энтропии (entropy reduction) Error: Reference source not found. В качестве атрибута разбиения используется атрибут, который обеспечивает наибольший прирост информации Error: Reference source not found
Основной недостаток алгоритма ID3 – тенденция к переобучению и как следствие – сверхчувствительность (overfitting) к часто повторяющимся значениям.
Данная проблема решается использованием рассмотренного ранее критерия отношения прироста информации (gain‑ratio). В критерии используется отношение полного прироста информации после разбиения к оценке потенциальной информации, созданной при разбиении.
30. Алгоритм c4.5 построения дерева решений
Критерий отношения прироста информации (gain‑ratio) строится по формуле Error: Reference source not found
где определяется по Error: Reference source not found.
При разбиении выбирается атрибут, обеспечивающий максимум .
Поясним эффект от введения GainRatio. Если в результате разбиения получается большое число подмножеств с небольшим числом примеров, что характерно для переобучения, то параметр SplitInfo растет. Поскольку SplitInfo стоит в знаменателе выражения для GainRatio, то GainRatio для такого разбиения уменьшается. Благодаря этому атрибут, для которого параметр SplitInfo растет, имеет меньше шансов быть выбранным для разбиений, чем при использовании обычного Gain-критерия.
Используем критерия отношения прироста информации для нашего примера (табл. 4.10). Найдем прирост информации для разбиения
Так как (см. Error: Reference source not found), то
Аналогичная процедура должна быть выполнена для остальных разбиений в дереве решений.
Алгоритм может создавать узлы и листья, содержащие незначительное количество примеров. Чтобы избежать такой ситуации используют эмпирическое правило [4]: при разбиении множества, по крайней мере два подмножества должны иметь не меньше заданного минимального количества объектов (обычно, не меньше двух). Если данное правило не выполняется, то дальнейшее разбиение этого множества прекращается и соответствующий узел отмечается как лист. При этом в листьях могут присутствовать объекты разных классов. Тогда в качестве решения листа выбирается класс, наиболее часто встречающийся в узле. Если в листе присутствует равное число примеров нескольких классов, то решение дает класс, наиболее часто встречающийся у непосредственного предка данного листа.
Алгоритм C4.5 включает процедуру работы с пропущенными данными. В алгоритме С4.5 предполагается, что наблюдения с неизвестными значениями имеют статистическое распределение соответствующего атрибута согласно относительной частоте появления известных значений. Например, рассмотрим множество наблюдений из табл. 4.10, в котором отсутствует значение атрибута в строке 6.
Источник
Построение решающих деревьев жадным алгоритмом ID3
На предыдущем занятии мы с вами познакомились с критериями выбора предикатов для разбиения множества данных в вершинах решающего дерева. В первую очередь – это impurity (информативность, мера неопределенности), обозначим ее через
где — выборка, попавшая в текущую вершину. И показатель качества разбиения, который часто вычисляется как информационный выигрыш:
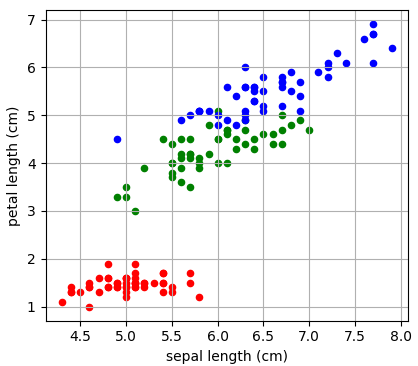
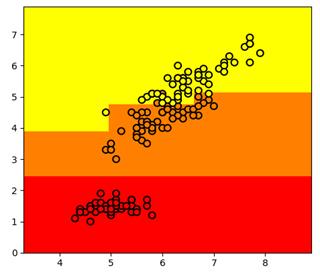
Давайте теперь воспользуемся этими показателями для построения бинарного решающего дерева. В качестве обучающей выборки возьмем 150 объектов трех классов ирисов (50 в каждом классе), распределенных в двумерном признаковом пространстве: длина и ширина лепестков:
То есть, входные векторы будут иметь два числовых признака:
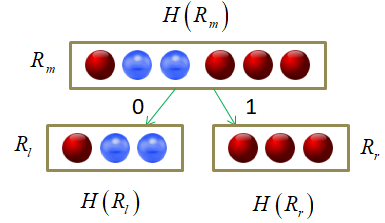
Существует несколько распространенных алгоритмов построения решающих деревьев. Вначале я рассмотрю самый простой, который называется ID3 (Iterative Dichotomiser 3), разработанный Россом Куинланом в 1986 году для задачи классификации. Этот алгоритм использует энтропию в качестве информативности и реализует жадную стратегию, то есть, в каждом узле дерева, начиная с корневого, находит такой признак j и такой порог t, которые дают наибольшее значение показателя :
Затем, построение рекурсивно повторяется для каждой новой вершины.
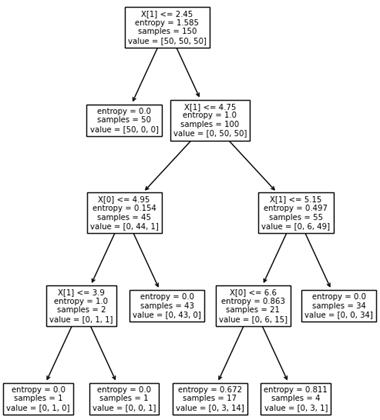
Вот пример разбиения обучающего множества деревом глубиной 4. Само дерево имеет вид:
Отсюда хорошо видно, как происходило разбиение. Вначале были отделены все красные объекты выборки по второму признаку (длина лепестка) с порогом t = 2,45 и предикатом:
Если предикат выполняется, то попадаем в листовую вершину с нулевой энтропией и 50-ю представителями класса «красных» объектов. Во вторую вершину попадает 100 объектов двух других классов с энтропией, равной 1. Далее, мы делим объекты второй вершины дерева также по второму признаку и уровню 4,75. Формируются следующие две вершины. И так далее, пока либо не будет достигнута нулевая энтропия и сформирован лист дерева, либо глубина дерева достигнет уровня 4. (Этот максимальный уровень был задан при генерации данного решающего дерева.) В каждой листовой вершине мы сохраняем метку класса с наибольшим числом представителей.
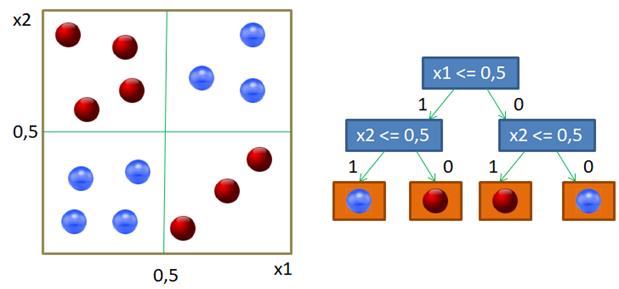
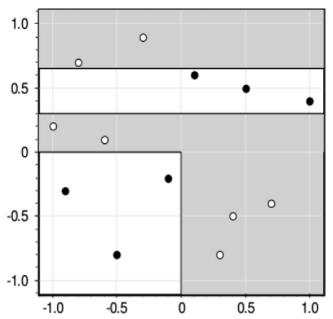
Вот наглядный пример работы жадного алгоритма ID3. Казалось бы, все прекрасно и ничто не мешает нам использовать его в самых разных задачах. Однако, практика показала, что жадная стратегия построения деревьев часто не самая лучшая. Простой контрпример – задача XOR, когда объекты двух классов сосредоточены в разных углах квадрата:
Жадная стратегия дает, следующее решающее дерево:
Но, тем не менее, алгоритм ID3 относительно прост в реализации, а потому является основой для более сложных подходов к построению решающих деревьев, о которых мы поговорим на следующих занятиях.
Критерии останова (методы регуляризации)
- impurity равна нулю или меньше некоторого заданного значения;
- число объектов в вершине меньше заданной величины;
- вероятность правильной классификации объекта больше заданной величины;
- достигнуто максимальное количество листьев в дереве;
- достигнута максимальная заданная глубина дерева.
Преимущества и недостатки жадной стратегии
Итак, я думаю, в целом идея построения решающих деревьев по алгоритму ID3 вам понятна. В заключение отмечу преимущества и недостатки такого подхода.
Достоинства:
- Интерпретируемость и простота классификации (легко объяснить результат классификации эксперту).
- Допустимы разнотипные данные и пропуски в данных.
- Не бывает отказов от классификации.
Недостатки:
- Жадная стратегия в большинстве задач излишне усложняет структуру дерева, то есть, приводит к его переобучению.
- Чем дальше от корня дерева, тем меньше объектов в листовых вершинах, а значит, ниже статистическая надежность различных показателей, например, вероятности появления того или иного класса.
- Высокая чувствительность к шуму в объектах выборки и критерию информативности (impurity).
Источник