Алгоритм построения идеально сбалансированного дерева

Алгоритм построения идеально сбалансированного дерева

На этом шаге мы рассмотрим построение идеально сбалансированных бинарных деревьев .

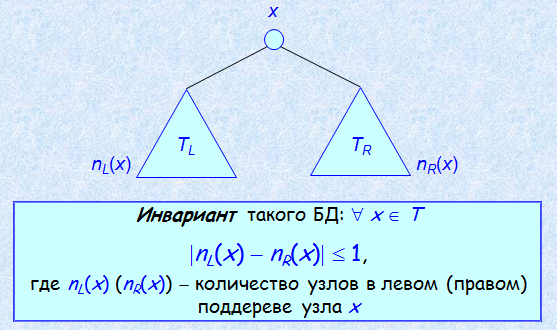
Пусть требуется построить бинарное дерево с n узлами и минимальной высотой (максимально «ветвистое» и «низкое»). Такие деревья имеют большое практическое значение, так как их использование сокращает машинное время, требуемое на выполнение различных алгоритмов. Определение. Бинарное дерево назовем идеально сбалансированным , если для каждой его вершины количество вершин в левом и правом поддереве различаются не более чем на 1 .

Изобразим несколько идеально сбалансированных деревьев:

Рис.1. Примеры идеально сбалансированных бинарных деревьев

Теорема. Длина внутреннего пути в идеально сбалансированном дереве, содержащем n вершин, не превосходит величины: (n+1)[log 2 n] — 2 * 2 [log 2 n] — 2

Доказательство. Ясно, что только одна вершина (а именно корень) может находиться на нулевом расстоянии от корня; не более двух вершин могут находиться на расстоянии 1 от корня; не более четырех вершин могут находиться от корня на расстоянии, равном 2 и т.д. Мы видим, что длина внутреннего пути всегда не больше суммы первых n членов ряда:

Рис.2. Длина внутреннего пути

Взгляните на следующее соотношение:

k 1 2 3 4 5 6 7 8 9 10 11 12 13 . [log2k] 0 1 1 2 2 2 2 3 3 3 3 3 3 .

Теперь легко понять, что сумма первых n членов равна:

символы [ ] — обозначение операции выделения целой части числа.

откуда и следует утверждение теоремы.

Алгоритм построения идеально сбалансированного дерева при известном числе вершин n лучше всего формулируется с помощью рекурсии [1,с.226]. При этом необходимо лишь учесть, что для достижения минимальной высоты при заданном числе вершин, нужно располагать максимально возможное число вершин на всех уровнях, кроме самого нижнего. Это можно сделать очень просто, если распределять все поступающие в дерево вершины поровну слева и справа от каждой вершины.

• взять одну вершину в качестве корня.
• построить левое поддерево с nl = n DIV 2 вершинами тем же способом.
• построить правое поддерево с nr = n-nl-1 вершинами тем же способом.

Оформим описанный алгоритм в виде рекурсивной функции:

node *Tree (int n, node **p) // Построение идеально сбалансированного дерева с n вершинами. // *p - указатель на корень дерева. < node *now; int x,nl,nr; now = *p; if (n==0) *p = NULL; else < nl = n/2; nr = n - nl - 1; cin>>x; now = new(node);(*now).Key = x; Tree (nl,&((*now).Left)); Tree (nr,&((*now).Right)); *p = now;> >

Приведем пример программы, иллюстрирующей построение идеально сбалансированного дерева (рекурсивный алгоритм).

#include struct node < int Key; int Count; node *Left; node *Right; >; class TREE < private: node *duk; //Корень дерева. public: TREE() < duk = NULL; > node **GetDuk() < return &duk; > node *Tree (int, node **); void Vyvod (node **, int); >; void main () < TREE A; int n; cout>n; cout node *TREE::Tree (int n,node **p) // Построение идеально сбалансированного // дерева с n вершинами. // *p - указатель на корень дерева. < node *now; int x,nl,nr; now = *p; if (n==0) *p = NULL; else < nl = n/2; nr = n - nl - 1; cin>>x; now = new(node); (*now).Key = x; Tree (nl,&((*now).Left)); Tree (nr,&((*now).Right)); *p = now; > > void TREE::Vyvod (node **w,int l) // Изображение бинарного дерева, заданного // указателем *w на экране дисплея. < if (*w!=NULL) < Vyvod (&((**w).Right),l+1); for (int i=1; i >

Отметим простоту и ясность этой программы, достигнутые благодаря использованию рекурсивных процедур. Очевидно, что рекурсивные алгоритмы особенно уместны, когда программа должна обрабатывать данные, структура которых определена рекурсивно.

Предположим, например, что имеется следующий набор ключей для построения дерева с 21 вершиной: 8, 9, 11, 15, 19, 20, 21, 7, 3, 2, 1, 5, 6, 4, 13, 14, 10, 12, 17, 16, 18. Результат работы программы следующий:

Рис.3. Результат работы приложения

Замечание . Идеально сбалансированные деревья изобретены для сокращения времени работы вычислительных алгоритмов, связанных с необходимостью частого прохода по ветвям дерева (напомним, что ветвь — это путь от корня дерева до листа). Одним из примеров подобного рода алгоритмов является поиск информации в дереве. В случае, если дерево является идеально сбалансированным, поиск осуществляется так же быстро, как и при дихотомии, то есть для поиска придется перебрать не более log 2 n вершин, где n — число вершин в дереве.

Одно «но»: при формировании идеально сбалансированного дерева ключи необходимо вводить в отсортированном по возрастанию (по убыванию) виде. В этом случае можно построить достаточно простой алгоритм поиска в идеально сбалансированном дереве вершины с заданным ключом. (1) Вирт H. Алгоритмы + структуры данных = программы. — М.: Мир, 1985. — 406 с.
(2) Кнут Д. Искусство программирования для ЭВМ. Т.1: Основные алгоритмы. — M.: Мир, 1976. — 736 с.

На следующем шаге мы разберем балансированные по высоте деревья .

Источник

Идеально сбалансированные бинарные деревья. (Лек 8).

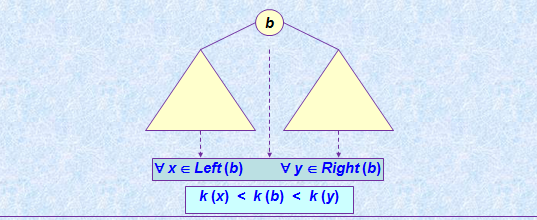
Бинарное дерево называется бинарным деревом поиска (БДП), если в каждом его узле выполняется следующее условие: пусть k – значение ключа в этом узле, тогда в левом поддереве этого узла нет узлов с ключами, большими или равными k, а в правом поддереве – нет узлов с ключами, меньшими или равными k. Формально это условие можно записать в виде утверждения (инварианта БДП T: BTree):

( b  T: (not Null (Left (b)))  ( x  Left (b): k(x) < k(b)))

(not Null (Right (b)))  ( y  Right (b): k(b) < k(y)))),

а графически изобразить в виде рисунка

Инвариант БДП (T: BSTree):

Пусть k – значение ключа в узле, тогда в левом поддереве этого узла нет узлов с ключами, большими или равными k, а в правом поддереве – нет узлов с ключами, меньшими или равными k.

И это верно для каждого узла дерева.

( b  T:

(not Null (Left (b)))  ( x  Left (b): k(x) < k(b)))

(not Null (Right (b)))  ( y  Right (b): k(b) < k(y))))

Операция поиска заданного элемента x: base

в непустом БДП b: BSTree производится рекурсивно :

Если k(x) = k(b), то элемент x находится в корне дерева b. Поиск закончен «успешно» – элемент найден.

Если k(x) > k(b), то продолжить поиск в правом поддереве Right (b).

Если выбранное поддерево оказывается пустым, то поиск завершается «неудачно» – элемента x в дереве b нет.

Операция поиска заданного элемента x: base

в непустом БДП b: binTree

binTree Locate (base x, binTree b)

// b – должно быть БДП

if (isNull(b)) return NULL;

else return Locate(x,Right(b));

Поскольку в этой рекурсивной функции каждый экземпляр порождает (альтернативно) не более одного следующего рекурсивного вызова, то рекурсия легко преобразуется в итерацию:

if (x==r) found = true; // b — искомый узел

else return NULL;

Выход из цикла при found = false говорит об отсутствии в дереве искомого элемента, при этом возвращается NULL

Более короткий вариант того же цикла

(без переменных r и found, но предполагающий режим неполного вычисления булевских выражений) есть

while (!isNull(b) && !(x==RootBT(b)))

Источник

Двоичные (бинарные) деревья

Т.е., двоичным деревом называют конечный набор элементов, являющихся узлами (вершинами) дерева, такой, что:

а) Т – это пустое или нулевое дерево,

б) Т состоит из корня (вершины) с двумя отдельными двоичными деревьями, называющимися соответственно левым и правым поддеревьями.

Деревья степени больше 2 называют сильно ветвящимися деревьями.

Пример: Представление троичного дерева в виде двоичного.

 сын сын брат Двоичными деревьями можно представлять алгебраические выражения. Например, выражение (a + b * c) * (d – e / f) представляется в виде: Двоичные деревья (2-Д) используются: б) в представлении генеалогических деревьев, в) в описании турниров и т.п. 2-Д является полным, если все его уровни, кроме последнего, имеют по 2 узла и все нижние узлы имеют хотя бы левого сына. Глубина полного 2-Д с n узлами: , : Dn=log₂n+ 1, например, при n= 10, тоDn= 21. Идеально сбалансированное дерево – это дерево, у которого количествовершин в левом и правом поддеревьях отличается не более, чем на 1. Для построения ИСД используется рекурсия.

2. Алгоритм построения идеально сбалансированного дерева

   1. Взять одну вершину в качестве корня;
   2. Построить левое поддерево с nl=ndiv2 (где n – количество всех вершин) узлами тем же способом;
   3. Построить правое поддерево с nr=n–nl– 1 вершинами тем же способом.

   Inf : Type_Inf;

   Var NewNode:p_Tr;

   Nl,Nr:Integer; Begin If N=0 Then Tree ← пусто Else Nl ← N div 2 Nr ← N-Nl-1 Создать новую вершину (NewNode) В поле данных ← данные Left ← Tree(Nl) Rigt ← Tree(Nr) Tree ← NewNode End; Иллюстрация построения идеально сбалансированного дерева: n= 1 сначала строим левое поддерево с  ndiv2 узлами   n= 2 n=3 начинаем строить процесс  правое поддерево   повторяется  с n–nl– 1 узлами несколько раз, после чего имеем n= 4  идеально сбалансированное дерево: Графическое представление Два двоичных дерева: «Обычное» (левые и правые сыновья различаются. ) дерево:

   Источник

   Идеально сбалансированное дерево поиска

Двоичное дерево называется идеально сбалансированным (ИСД), если для каждой его вершины размеры левого и правого поддеревьев отличаются не более чем на 1. На рисунке приведены примеры деревьев, одно из которых является идеально сбалансированным, а другое – нет. Рисунок 4 Примеры ИСД и неИСД Отметим некоторые свойства идеально сбалансированного дерева. Свойство 1.Высота ИСД сnвершинами минимальна и равнаh_ИСД(n)= h_min(n) =log(n+1). Свойство 2.Если дерево идеально сбалансировано, то все его поддеревья также идеально сбалансированы. Задача построения идеально сбалансированного дерева поиска из элементов массива А = (а₁, а₂, … , а_n) решается в два этапа:

1. Сортировка массива А.
2. В качестве корня дерева возьмем средний элемент отсортированного массива, из меньших элементов массива строим левое поддерево, из больших – правое поддерево. Далее процесс построения продолжается до тех пор, пока левое или правое поддерево не станет пустым.

Пример. Построить ИСДП из элементов массива А. Пусть n = 16, а элементы массива это числа в 16-ричной системе счисления. А: В 9 2 4 1 7 Е F A D C 3 5 8 6 А_упор:1 2 3 4 5 6 7 8 9 А В С D E F Рисунок 5 Построение ИСДП Приведем на псевдокоде алгоритм построения ИСДП. Функция ИСДП (L, R) возвращает указатель на построенное дерево, где L, R – левая и правая границы той части массива, из элементов которой строится дерево.

Алгоритм на псевдокоде

Контрольные вопросы

1. Дайте определение двоичного дерева поиска.
2. Что такое идеально сбалансированное дерево поиска?
3. Какова высота ИСДП?
4. Каким образом строится ИДСП?

Случайное дерево поиска

Определение случайного дерева поиска

При решении многих типов задач объем данных заранее неизвестен, но необходима такая структура данных, для которой достаточно быстро выполняются операции поиска, добавления и удаления вершин. Одно из решений этой проблемы построение случайного дерева поиска (СДП). При построении СДП данные поступают последовательно в произвольном порядке и добавление нового элемента происходит в уже имеющееся дерево. Пример случайного дерева поиска для последовательности D: B 9 2 4 1 7 E F A D C 3 5 8 6 приведен на рисунке 6. Рисунок 6 Случайное дерево поиска Это дерево не является ИСДП. В худшем случае СДП может выродиться в список. Пример. 1) D: 1 2 3 4 5 2) D: 5 1 2 4 3 Рисунок 7 Плохие СДП Таким образом, средняя высота случайного дерева поиска может изменяться в пределах log n< h_срcд< n при больших n. В [1] показано, что ( h_{ср сд} / h_{ср исдп}) = 2ln 2 = 1,386. и h_{ср сд} =О(log n) при n→∞.

Источник

Читайте также:  Резьба по дереву резцами виде