Алгоритм сортировки бинарные деревья

Анализ алгоритма сортировки бинарным деревом поиска

Первая мысль, которая возникает при начальном знакомстве с этим методом — сильная зависимость структуры дерева от входных данных. Если данные абсолютно случайны (например, массив формировался при помощи датчика случайных чисел), то дерево получится достаточно плотным, как на рисунке 4.5. При построении такого дерева можно значительно выиграть во времени на сокращении количества сравнений при поиске места для каждого нового листа. В самом лучшем случае потребуется log₂n сравнений на каждый добавляемый элемент, следовательно, временная сложность построения дерева из n элементов составит O(nlogn).

Но если входная последовательность уже была отсортирована, то дерево выродится в линейный список (перемещаясь по дереву, будем двигаться все время по одной ветви). Сам процесс построения вырожденного дерева потребует столько же времени, сколько и простые методы сортировки — O(n 2 ). Для того, чтобы исключить возможность получения вырожденного дерева или дерева с низкой плотностью, можно хорошенько «перемешать» исходные данные перед тем, как их сортировать, но на это опять потребуется лишнее время.

Такое поведение алгоритма следует оценить как неестественное. Устойчивости также нет. Есть и еще один крупный недостаток этого метода — большие требования к памяти под дерево. Кроме места под значения элементов требуется память на 2 указателя для каждого из них.

В силу этих недостатков данный способ не находит практического применения в тех случаях, когда требуется просто отсортировать массив или список в оперативной памяти. Но не нужно забывать, что основное назначение бинарного дерева поиска — быстрый поиск данных. Поэтому, если бинарное дерево поиска строилось непосредственно при считывании данных с диска, чтобы затем использовать его для задач поиска, то это наилучший способ получить данные в отсортированном виде.

Подробно реализацию бинарного дерева поиска рассмотрим в следующей главе. Наибольшего внимания из древовидных методов заслуживает пирамидальная сортировка, поэтому рассмотрим ее подробнее.

4.3.2. Пирамидальная сортировка

В алгоритме пирамидальной сортировки используется специальная структура данных — пирамида (иногда её также называют кучей, англ. heap). Пирамидой называется двоичное дерево, в вершинах которого размещаются заданные нам элементы. При этом должны выполняться следующие требования:

• все уровни, за исключением последнего, должны быть заполнены полностью
• последний уровень (т.е. уровень листьев дерева) может быть заполнен частично, но обязательно слева направо без пропусков
• основное свойство пирамиды: ни один элемент в пирамиде не может быть больше своего родителя

Очевидно, что на вершине пирамиды находится наибольший её элемент.

Для представления пирамиды в памяти удобно использовать массив, при этом пирамида хранится в массиве следующим образом. Сыновья элемента с индексом i будут иметь индексы i*2+1 и i*2+2, а его родитель — индекс (i-1)/2 (напомним, что в языке C++ массивы начинаются с нуля, а при делении двух целых чисел дробная часть отбрасывается). Так, для вышеприведённого рисунка пирамида будет храниться в массиве следующим образом:

Источник

Сортировка бинарным деревом

Сортировка бинарным деревом (Tree sort) – алгоритм сортировки, который заключается в построении двоичного дерева поиска по ключам массива, с последующим построением результирующего массива упорядоченных элементов путем обхода дерева.

Принцип работы алгоритма сортировки бинарным деревом

• Элементы неотсортированного массива данных добавляются в двоичное дерево поиска;
• Для получения отсортированного массива, производится обход бинарного дерева с переносом данных из дерева в результирующий массив.

Реализация алгоритма сортировки бинарным деревом

using System; using System.Collections.Generic; namespace TreeSortApp < //простая реализация бинарного дерева public class TreeNode < public TreeNode(int data) < Data = data; >//данные public int Data < get; set; > //левая ветка дерева public TreeNode Left < get; set; > //правая ветка дерева public TreeNode Right < get; set; > //рекурсивное добавление узла в дерево public void Insert(TreeNode node) < if (node.Data < Data) < if (Left == null) < Left = node; >else < Left.Insert(node); >> else < if (Right == null) < Right = node; >else < Right.Insert(node); >> > //преобразование дерева в отсортированный массив public int[] Transform(Listint> elements = null) < if (elements == null) < elements = new Listint>(); > if (Left != null) < Left.Transform(elements); >elements.Add(Data); if (Right != null) < Right.Transform(elements); >return elements.ToArray(); > > class Program < //метод для сортировки с помощью двоичного дерева private static int[] TreeSort(int[] array) < var treeNode = new TreeNode(array[0]); for (int i = 1; i < array.Length; i++) < treeNode.Insert(new TreeNode(array[i])); > return treeNode.Transform(); > static void Main(string[] args) < Console.Write("n hljs-keyword">var n = int.Parse(Console.ReadLine()); var a = new int[n]; var random = new Random(); for (int i = 0; i < a.Length; i++) < a[i] = random.Next(0, 100); > Console.WriteLine("Random Array: ", string.Join(" ", a)); Console.WriteLine("Sorted Array: ", string.Join(" ", TreeSort(a))); > > > 

Источник

2 Алгоритм бинарного дерева

Сортировка с помощью бинарного дерева — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например, с файла, сокета или консоли) [6].

Реализация алгоритма бинарного дерева на языке С#:

public TreeItem LeftChild;

public TreeItem RightChild;

TreeItem top; int n = 0;

private void Add(int a)

TreeItem temp = new TreeItem();

private void Build(TreeItem t)

public void Sort(int[] mas)

>

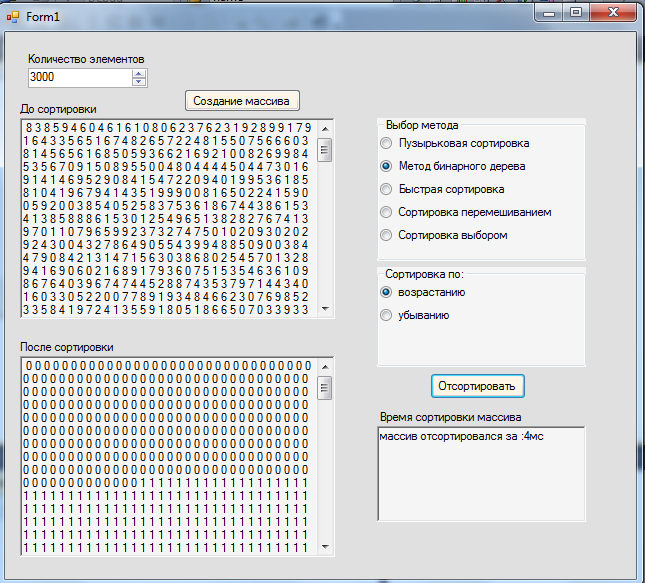
Рисунок 3 – Реализация программы, которая сортирует по возрастанию массив из 3000 элементов методом бинарного дерева за 4 миллисекунды.

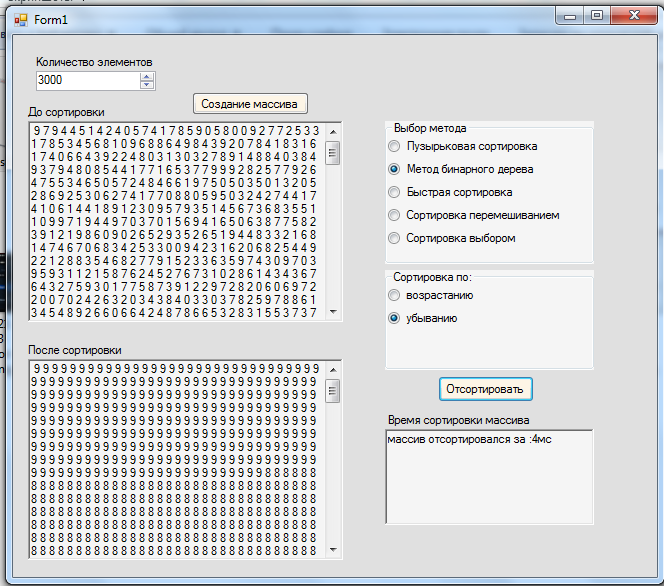
Рисунок 4 – Реализация программы, которая сортирует по убыванию массив из 3000 элементов методом бинарного дерева за 4 миллисекунды.

3 Быстрая сортировка

Основная стратегия ускорения алгоритмов сортировка — обмены между как можно более дальними элементами исходного файла — в методе быстрой сортировки реализована за счет того, что один из ключей в исходном файле используется для разделения его на два подфайла так, чтобы слева от выбранного элемента находились только элементы с меньшими ключами, а справа — только с большими. Элемент, разделяющий файл, помещается между его двумя подфайлами и процедура выполняется рекурсивно для каждой половины до тех пор, пока в очередном новом подфайле не окажется меньше, чем М элементов, где М — заранее выбранное число.

Сортировка подфайлов, содержащих меньше чем М элементов, выполняется каким-либо простым методом, например, простыми вставками. Таким образом, реализация метода зависит от двух параметров: значения М и способа выбора элемента, который предназначен для разделения файла на две части.

Блок выбора Х в простейшем случае формулируется как X=K[l], однако это может привести к крайне неэффективному алгоритму. Наиболее простое лучшее решение — выбирать Х как случайный ключ из диапазона K[l] . K[r] и обменять его с K[l] [4].

Реализация алгоритма быстрой сортировки на языке С#:

public void sorting(int[] mas, long first, long last)

int p = mas[(last — first) / 2 + first];

long i = first, j = last;

Источник