Дерево решений (Decision Trees)
Дерево решений — классификатор, построенный на основе решающих правил вида «если, то», упорядоченных в древовидную иерархическую структуру.
В основе работы дерева решений лежит процесс рекурсивного разбиения исходного множества объектов на подмножества, ассоциированные с предварительно заданными классами. Разбиение производится с помощью решающих правил, в которых осуществляется проверка значений атрибутов по заданному условию.
Строятся на основе обучения с учителем. В качестве обучающего набора данных используется множество наблюдений, для которых предварительно задана метка класса.
Структурно дерево решений состоит из объектов двух типов — узлов (node) и листьев (leaf). В узлах расположены решающие правила и подмножества наблюдений, которые им удовлетворяют. В листьях содержатся классифицированные деревом наблюдения: каждый лист ассоциируется с одним из классов, и объекту, который распределяется в лист, присваивается соответствующая метка класса.
Визуально узлы и листья в дереве хорошо различимы: в узлах указываются правила, разбивающие содержащиеся в нем наблюдения, и производится дальнейшее ветвление. В листьях правил нет, они помечаются меткой класса, объекты которого попали в данный лист. Ветвление в листьях не производится, и они заканчивают собой ветвь дерева (поэтому их иногда называют терминальными узлами).
Если класс, присвоенный деревом, совпадает с целевым классом, то объект является распознанным, в противном случае — нераспознанным. Самый верхний узел дерева называется корневым (root node). В нем содержится весь обучающий или рабочий набор данных.
Дерево решений является линейным классификатором, т.е. производит разбиение объектов в многомерном пространстве плоскостями (в двумерном случае — линиями).
Дерево, представленное на рисунке, решает задачу классификации объектов по двум атрибутам на три класса.
На рисунке кружки представляют объекты класса 1, квадраты — класса 2, а треугольники — класса 3. Пространство признаков разделено линиями на три подмножества, ассоциированных с классами. Эти же подмножества будут соответствовать и трем возможным исходам классификации. В классе «треугольников» имеются нераспознанные примеры («квадраты»), т.е. примеры, попавшие в подмножества, ассоциированные с другим классом.
Теоретически, алгоритм может генерировать новые разбиения до тех пор, пока все примеры не будут распознаны правильно, т.е. пока подмножества, ассоциированные с листьями, не станут однородными по классовому составу. Однако это приводит к усложнению дерева: большое число ветвлений, узлов и листьев усложняет его структуру и ухудшает его интерпретируемость. Поэтому на практике размер дерева ограничивают даже за счет некоторой потери точности. Данный процесс называется упрощением деревьев решений и может быть реализован с помощью методов ранней остановки и отсечения ветвей.
Деревья решений являются жадными алгоритмами. Могут быть дихотомичными (бинарными), имеющими только два потомка в узле, и полихотомичными — имеющими более 2-х потомков в узле. Дихотомичные деревья являются более простыми в построении и интерпретации.
В настоящее время деревья решений стали одним из наиболее популярных методов классификации в интеллектуальном анализе данных и бизнес-аналитике. Поэтому они входят в состав практически любого аналитического ПО.
Разработано большое количество различных алгоритмов построения деревьев решений. Наиболее известным является семейство алгоритмов, основанное на критерии прироста информации (information gain) — ID3, C4.5, С5.0, — предложенное Россом Куинленом в начале 1980-х.
Также широкую известность приобрел алгоритм CART (Classification and Regression Tree — дерево классификации и регрессии), который, как следует из названия, позволяет решать не только задачи классификации, но и регрессии. Алгоритм предложен Лео Брейманом в 1982 г.
Широкая популярность деревьев решений обусловлена следующими их преимуществами:
- правила в них формируются практически на естественном языке, что делает объясняющую способность деревьев решений очень высокой;
- могут работать как с числовыми, так и с категориальными данными;
- требуют относительно небольшой предобработки данных, в частности, не требуют нормализации, создания фиктивных переменных, могут работать с пропусками;
- могут работать с большими объемами данных.
Вместе с тем, деревьям решений присущ ряд ограничений:
- неустойчивость — даже небольшие изменения в данных могут привести к значительным изменениям результатов классификации;
- поскольку алгоритмы построения деревьев решений являются жадными, они не гарантируют построения оптимального дерева;
- склонность к переобучению.
В настоящее время деревья решений продолжают развиваться: создаются новые алгоритмы (SHAID, MARS, Random Forest) и их модификации, изучаются проблемы построения ансамблей моделей на основе деревьев решений.
Деревья решений становятся важным инструментом управления бизнес-процессами и поддержки принятия решений. Общие принципы работы и области применения описаны в статье «Деревья решений: общие принципы».
Источник
Классификация и регрессия с помощью деревьев принятия решений
В данной статье сделан обзор деревьев принятия решений (Decision trees) и трех основных алгоритмов, использующих эти деревья для построение классификационных и регрессионных моделей. В свою очередь будет показано, как деревья принятия решения, изначально ориентированные на классификацию, используются для регрессии.
Деревья принятия решений
Дерево принятия решений — это дерево, в листьях которого стоят значения целевой функции, а в остальных узлах — условия перехода (к примеру “ПОЛ есть МУЖСКОЙ”), определяющие по какому из ребер идти. Если для данного наблюдения условие истина то осуществляется переход по левому ребру, если же ложь — по правому.
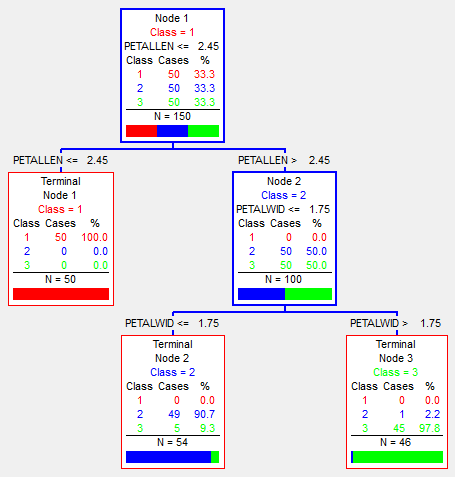
Классификация
На изображении приведенном выше показано дерево классификации ирисов. Классификация идет на три класса (на изображении помечены — красным, синим и зеленым), и проходит по параметрам: длина\толщина чашелистика (SepalLen, SepalWid) и длина\толщина лепестка (PetalLen, PetalWid). Как видим, в каждом узле стоит его принадлежность к классу (в зависимости от того, каких элементов больше попало в этот узел), количество попавших туда наблюдений N, а так же количество каждого класса. Так же не в листовых вершинах есть условие перехода — в одну из дочерних. Соответственно, по этим условиям и разбивается выборка. В результате, это дерево почти идеально (6 из 150 неправильно) классифицировало исходные данные (именно исходные — те на которых оно обучалось).
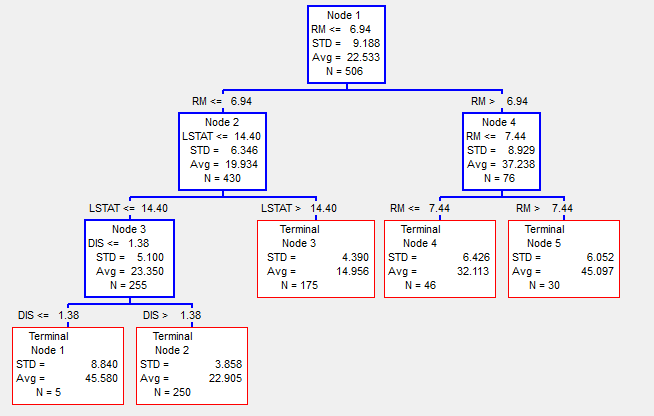
Регрессия
Если при классификации в листах стоят результирующие классы, при регрессии же стоит какое-то значение целевой функции.
На выше приведенном изображении регрессионное дерево, для определения цены на землю в городе Бостон в 1978 году, в зависимости от параметров RM — количество комнат, LSTAT — процент неимущих и нескольких других параметров (более детально можно посмотреть в [4]). Соответственно, здесь в каждом узле мы видим среднее значение (Avg) и стандартное отклонение (STD) значений целевой функции наблюдений попавших в эту вершину. Общее количество наблюдений попавших в узел N. Результатом регрессии будет то значение среднего (Avg), в какой узел попадёт наблюдение.
Таким образом изначально классификационное дерево, может работать и для регрессии. Однако при таком подходе, обычно требуются большие размеры дерева, чем при классификации, что бы достигнуть хороших результатов регрессии.
Основные методы
Ниже перечислены несколько основных методов, которые используют деревья принятия решений. Их краткое описание, плюсы и минусы.
CART
CART (англ. Classification and regression trees — Классификационные и регрессионные деревья) был первым из методов, придуманный в 1983 четверкой известных ученых в области анализа данных: Leo Breiman, Jerome Friedman, Richard Olshen and Stone [1].
Суть этого алгоритма состоит в обычном построении дерева принятия решений, не больше и не меньше.
На первой итерации мы строим все возможные (в дискретном смысле) гиперплоскости, которые разбивали бы наше пространство на два. Для каждого такого разбиения пространства считается количество наблюдений в каждом из подпространств разных классов. В результате выбирается такое разбиение, которое максимально выделило в одном из подпространств наблюдения одного из классов. Соответственно, это разбиение будет нашим корнем дерева принятия решений, а листами на данной итерации будет два разбиения.
На следующих итерациях мы берем один худший (в смысле отношения количества наблюдений разных классов) лист и проводим ту же операцию по разбиению его. В результате этот лист становится узлом с каким-то разбиением, и двумя листами.
Продолжаем так делать, пока не достигнем ограничения по количеству узлов, либо от одной итерации к другой перестанет улучшаться общая ошибка (количество неправильно классифицированных наблюдений всем деревом). Однако, полученное дерево будет “переобучено” (будет подогнано под обучающую выборку) и, соответственно, не будет давать нормальные результаты на других данных. Для того, что бы избежать “переобучения”, используют тестовые выборки (либо кросс-валидацию) и, соответственно, проводится обратный анализ (так называемый pruning), когда дерево уменьшают в зависимости от результата на тестовой выборке.
Относительно простой алгоритм, в результате которого получается одно дерево принятия решений. За счет этого, он удобен для первичного анализа данных, к примеру, что бы проверить на наличие связей между переменными и другим.
Быстрое построение модели
Легко интерпретируется (из-за простоты модели, можно легко отобразить дерево и проследить за всеми узлами дерева)
Часто сходится на локальном решении (к примеру, на первом шаге была выбрана гиперплоскость, которая максимально делит пространство на этом шаге, но при этом это не приведёт к оптимальному решению)
RandomForest
Random forest (Случайный лес) — метод, придуманный после CART одним из четверки — Leo Breiman в соавторстве с Adele Cutler [2], в основе которого лежит использование комитета (ансамбля) деревьев принятия решений.
Суть алгоритма, что на каждой итерации делается случайная выборка переменных, после чего, на этой новой выборке запускают построение дерева принятия решений. При этом производится “bagging” — выборка случайных двух третей наблюдений для обучения, а оставшаяся треть используется для оценки результата. Такую операцию проделывают сотни или тысячи раз. Результирующая модель будет будет результатом “голосования” набора полученных при моделировании деревьев.
Высокое качество результата, особенно для данных с большим количеством переменных и малым количеством наблюдений.
Возможность распараллелить
Не требуется тестовая выборка
Каждое из деревьев огромное, в результате модель получается огромная
Долгое построение модели, для достижения хороших результатов.
Сложная интерпретация модели (Сотни или тысячи больших деревьев сложны для интерпретации)
Stochastic Gradient Boosting
Stochastic Gradient Boosting (Стохастическое градиентное добавление) — метод анализа данных, представленный Jerome Friedman [3] в 1999 году, и представляющий собой решение задачи регрессии (к которой можно свести классификацию) методом построения комитета (ансамбля) “слабых” предсказывающих деревьев принятия решений.
На первой итерации строится ограниченное по количеству узлов дерево принятия решений. После чего считается разность между тем, что предсказало полученное дерево умноженное на learnrate (коэффициент “слабости” каждого дерева) и искомой переменной на этом шаге.
Yi+1=Yi-Yi*learnrate
И уже по этой разнице строится следующая итерация. Так продолжается, пока результат не перестанет улучшаться. Т.е. на каждом шаге мы пытаемся исправить ошибки предыдущего дерева. Однако здесь лучше использовать проверочные данные (не участвовавшие в моделировании), так как на обучающих данных возможно переобучение.
Высокое качество результата, особенно для данных с большим количеством наблюдений и малым количеством переменных.
Сравнительно (с предыдущим методом) малый размер модели, так как каждое дерево ограничено заданными размерами.
Сравнительно (с предыдущим методом) быстрое время построение оптимальное модели
Требуется тестовая выборка (либо кросс-валидация)
Невозможность хорошо распараллелить
Относительно слабая устойчивость к ошибочным данным и переобучению
Сложная интерпретация модели (Так же как и в Random forest)
Заключение
Список литературы
- “Classification and Regression Trees”. Breiman L., Friedman J. H., Olshen R. A, Stone C. J.
- “Random Forests”. Breiman L.
- “Stochastic Gradient Boosting”. Friedman J. H.
- http://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html
Источник