Алгоритмы обхода деревьев графа

Обход графа: поиск в глубину и поиск в ширину простыми словами на примере JavaScript

Простыми словами, обход графа — это переход от одной его вершины к другой в поисках свойств связей этих вершин. Связи (линии, соединяющие вершины) называются направлениями, путями, гранями или ребрами графа. Вершины графа также именуются узлами.

Двумя основными алгоритмами обхода графа являются поиск в глубину (Depth-First Search, DFS) и поиск в ширину (Breadth-First Search, BFS).

Несмотря на то, что оба алгоритма используются для обхода графа, они имеют некоторые отличия. Начнем с DFS.

Поиск в глубину

DFS следует концепции «погружайся глубже, головой вперед» («go deep, head first»). Идея заключается в том, что мы двигаемся от начальной вершины (точки, места) в определенном направлении (по определенному пути) до тех пор, пока не достигнем конца пути или пункта назначения (искомой вершины). Если мы достигли конца пути, но он не является пунктом назначения, то мы возвращаемся назад (к точке разветвления или расхождения путей) и идем по другому маршруту.

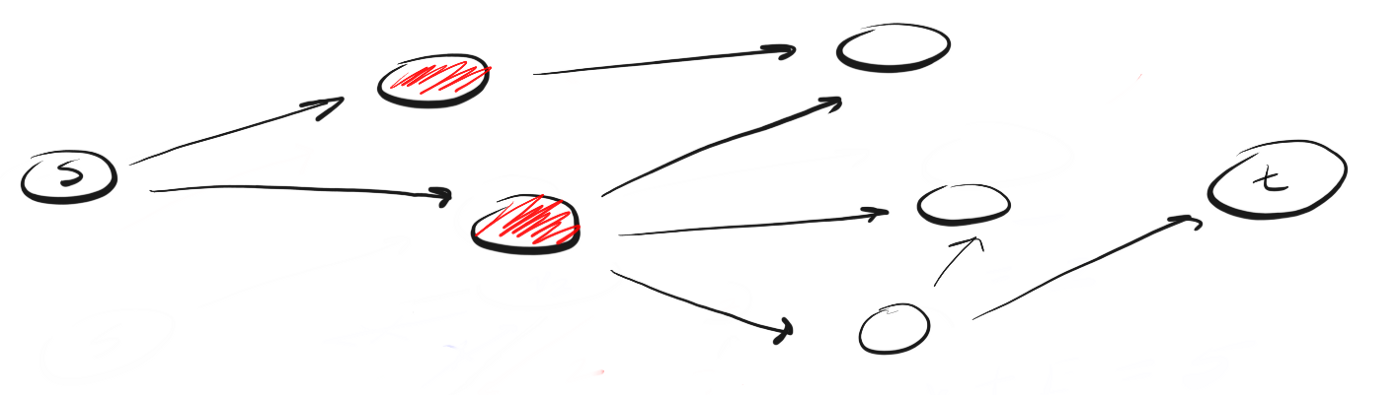
Давайте рассмотрим пример. Предположим, что у нас есть ориентированный граф, который выглядит так:

Мы находимся в точке «s» и нам нужно найти вершину «t». Применяя DFS, мы исследуем один из возможных путей, двигаемся по нему до конца и, если не обнаружили t, возвращаемся и исследуем другой путь. Вот как выглядит процесс:

Здесь мы двигаемся по пути (p1) к ближайшей вершине и видим, что это не конец пути. Поэтому мы переходим к следующей вершине.

Мы достигли конца p1, но не нашли t, поэтому возвращаемся в s и двигаемся по второму пути.

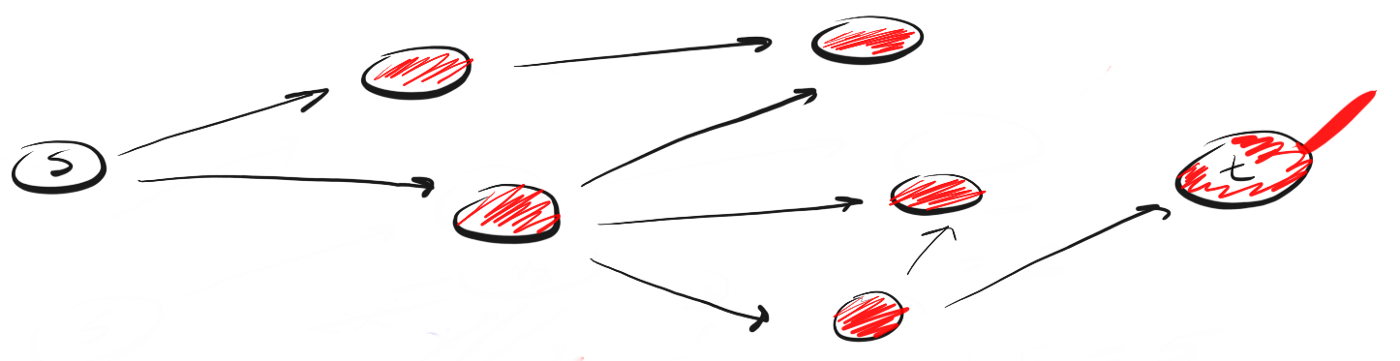
Достигнув ближайшей к точке «s» вершины пути «p2» мы видим три возможных направления для дальнейшего движения. Поскольку вершину, венчающую первое направление, мы уже посещали, то двигаемся по второму.

Мы вновь достигли конца пути, но не нашли t, поэтому возвращаемся назад. Следуем по третьему пути и, наконец, достигаем искомой вершины «t».

Так работает DFS. Двигаемся по определенному пути до конца. Если конец пути — это искомая вершина, мы закончили. Если нет, возвращаемся назад и двигаемся по другому пути до тех пор, пока не исследуем все варианты.

Мы следуем этому алгоритму применительно к каждой посещенной вершине.

Необходимость многократного повторения процедуры указывает на необходимость использования рекурсии для реализации алгоритма.

// при условии, что мы имеем дело со смежным списком // например, таким: adj = function dfs(adj, v, t) < // adj - смежный список // v - посещенный узел (вершина) // t - пункт назначения // это общие случаи // либо достигли пункта назначения, либо уже посещали узел if(v === t) return true if(v.visited) return false // помечаем узел как посещенный v.visited = true // исследуем всех соседей (ближайшие соседние вершины) v for(let neighbor of adj[v]) < // если сосед не посещался if(!neighbor.visited) < // двигаемся по пути и проверяем, не достигли ли мы пункта назначения let reached = dfs(adj, neighbor, t) // возвращаем true, если достигли if(reached) return true >> // если от v до t добраться невозможно return false > 

Заметка: этот специальный DFS-алгоритм позволяет проверить, возможно ли добраться из одного места в другое. DFS может использоваться в разных целях. От этих целей зависит то, как будет выглядеть сам алгоритм. Тем не менее, общая концепция выглядит именно так.

Анализ DFS

Давайте проанализируем этот алгоритм. Поскольку мы обходим каждого «соседа» каждого узла, игнорируя тех, которых посещали ранее, мы имеем время выполнения, равное O(V + E).

Краткое объяснение того, что означает V+E:

V — общее количество вершин. E — общее количество граней (ребер).

Может показаться, что правильнее использовать V*E, однако давайте подумаем, что означает V*E.

V*E означает, что применительно к каждой вершине, мы должны исследовать все грани графа безотносительно принадлежности этих граней конкретной вершине.

С другой стороны, V+E означает, что для каждой вершины мы оцениваем лишь примыкающие к ней грани. Возвращаясь к примеру, каждая вершина имеет определенное количество граней и, в худшем случае, мы обойдем все вершины (O(V)) и исследуем все грани (O(E)). Мы имеем V вершин и E граней, поэтому получаем V+E.

Далее, поскольку мы используем рекурсию для обхода каждой вершины, это означает, что используется стек (бесконечная рекурсия приводит к ошибке переполнения стека). Поэтому пространственная сложность составляет O(V).

Поиск в ширину

BFS следует концепции «расширяйся, поднимаясь на высоту птичьего полета» («go wide, bird’s eye-view»). Вместо того, чтобы двигаться по определенному пути до конца, BFS предполагает движение вперед по одному соседу за раз. Это означает следующее:

Вместо следования по пути, BFS подразумевает посещение ближайших к s соседей за одно действие (шаг), затем посещение соседей соседей и так до тех пор, пока не будет обнаружено t.

Чем DFS отличается от BFS? Мне нравится думать, что DFS идет напролом, а BFS не торопится, а изучает все в пределах одного шага.

Далее возникает вопрос: как узнать, каких соседей следует посетить первыми?

Для этого мы можем воспользоваться концепцией «первым вошел, первым вышел» (first-in-first-out, FIFO) из очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину, затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не опустеет или пока мы не найдем искомую вершину.

// при условии, что мы имеем дело со смежным списком // например, таким: adj = function bfs(adj, s, t) < // adj - смежный список // s - начальная вершина // t - пункт назначения // инициализируем очередь let queue = [] // добавляем s в очередь queue.push(s) // помечаем s как посещенную вершину во избежание повторного добавления в очередь s.visited = true while(queue.length >0) < // удаляем первый (верхний) элемент из очереди let v = queue.shift() // abj[v] - соседи v for(let neighbor of adj[v]) < // если сосед не посещался if(!neighbor.visited) < // добавляем его в очередь queue.push(neighbor) // помечаем вершину как посещенную neighbor.visited = true // если сосед является пунктом назначения, мы победили if(neighbor === t) return true >> > // если t не обнаружено, значит пункта назначения достичь невозможно return false > 

Анализ BFS

Может показаться, что BFS работает медленнее. Однако если внимательно присмотреться к визуализациям, можно увидеть, что они имеют одинаковое время выполнения.

Очередь предполагает обработку каждой вершины перед достижением пункта назначения. Это означает, что, в худшем случае, BFS исследует все вершины и грани.

Несмотря на то, что BFS может казаться медленнее, на самом деле он быстрее, поскольку при работе с большими графами обнаруживается, что DFS тратит много времени на следование по путям, которые в конечном счете оказываются ложными. BFS часто используется для нахождения кратчайшего пути между двумя вершинами.

Таким образом, время выполнения BFS также составляет O(V + E), а поскольку мы используем очередь, вмещающую все вершины, его пространственная сложность составляет O(V).

Аналогии из реальной жизни

Если приводить аналогии из реальной жизни, то вот как я представляю себе работу DFS и BFS.

Когда я думаю о DFS, то представляю себе мышь в лабиринте в поисках еды. Для того, чтобы попасть к цели мышь вынуждена много раз упираться в тупик, возвращаться и двигаться по другому пути, и так до тех пор, пока она не найдет выход из лабиринта или еду.

Упрощенная версия выглядит так:

В свою очередь, когда я думаю о BFS, то представляю себе круги на воде. Падение камня в воду приводит к распространению возмущения (кругов) во всех направлениях от центра.

Упрощенная версия выглядит так:

Выводы

• Поиск в глубину и поиск в ширину используются для обхода графа.
• DFS двигается по граням туда и обратно, а BFS распространяется по соседям в поисках цели.
• DFS использует стек, а BFS — очередь.
• Время выполнения обоих составляет O(V + E), а пространственная сложность — O(V).
• Данные алгоритмы имеют разную философию, но одинаково важны для работы с графами.

Источник

Реализуем алгоритм поиска в глубину

В этом туториале описан алгоритм поиска в глубину (depth first search, DFS) с псевдокодом и примерами. Кроме того, расписаны способы реализации поиска в глубину в C, Java, Python и C++.

“Поиск в глубину” или “обход в глубину” — это рекурсивный алгоритм по поиску всех вершин графа или дерева. Обход подразумевает под собой посещение всех вершин графа.

Алгоритм поиска в глубину

Стандартная реализация поиска в глубину помещает каждую вершину (узел, node) графа в одну из двух категорий:

Цель алгоритма состоит в том, чтобы пометить каждую вершину как “Пройденная”, избегая при этом циклов.

Алгоритм поиска в глубину работает следующим образом:

1. Начните с того, что поместите любую вершину графа на вершину стека.
2. Возьмите верхний элемент стека и добавьте его в список “Пройденных”.
3. Создайте список смежных вершин для этой вершины. Добавьте те вершины, которых нет в списке “Пройденных”, в верх стека.
4. Необходимо повторять шаги 2 и 3, пока стек не станет пустым.

Пример реализации поиска в глубину

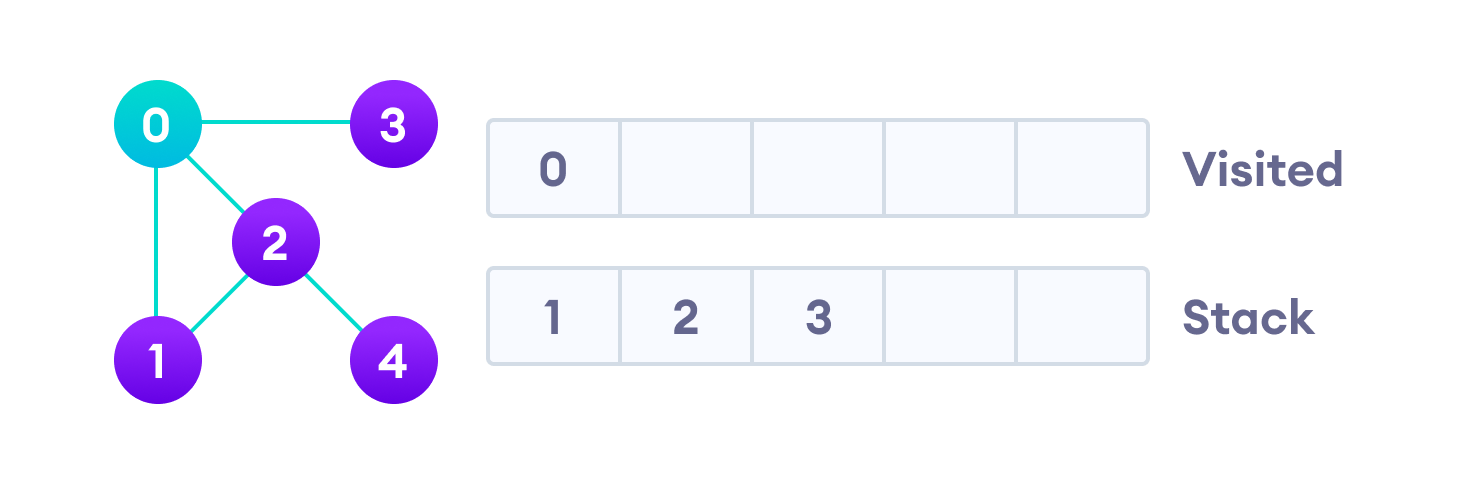
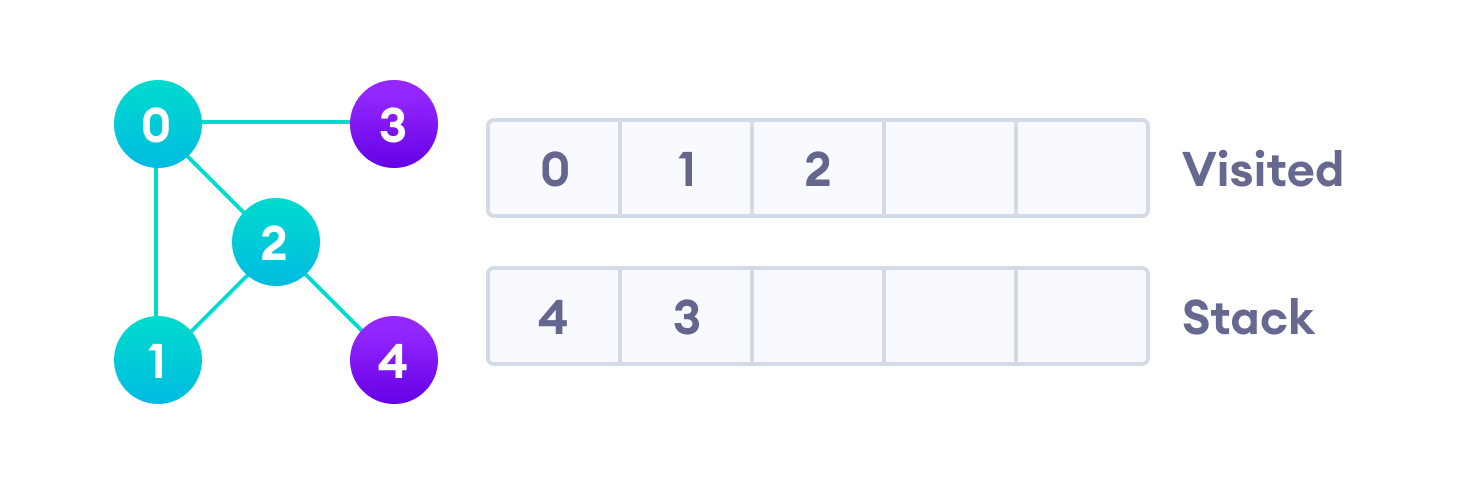
Предлагаю рассмотреть на примере, как работает алгоритм поиска в глубину. Мы будем использовать неориентированный граф с пятью вершинами.

Начнем мы с вершины “0”. В первую очередь алгоритм поиска в глубину поместит ее саму в список “Пройденные” (на изображении “Visited”), а ее смежные вершины — в стек.

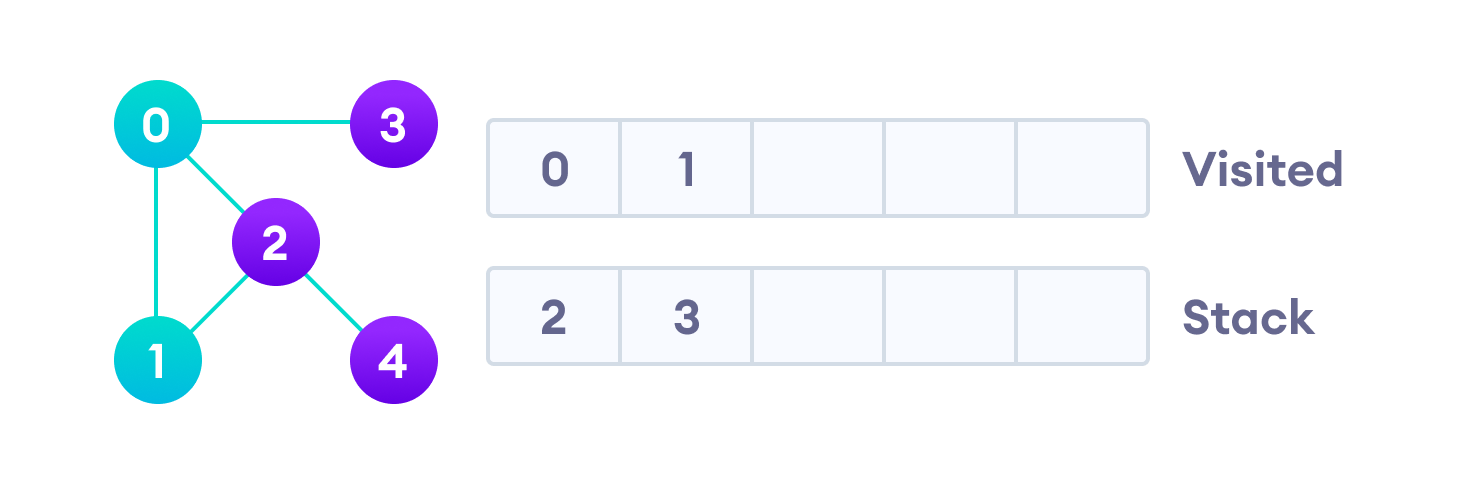
Затем мы берем следующий элемент сверху стека, т.е. к вершину “1”, и переходим к ее соседним вершинам. Поскольку вершина “0” уже пройдена, следующая вершина “2”.

Вершина “2” смежна непройденной вершине “4”, следовательно мы добавляем ее наверх стека и проходим ее.

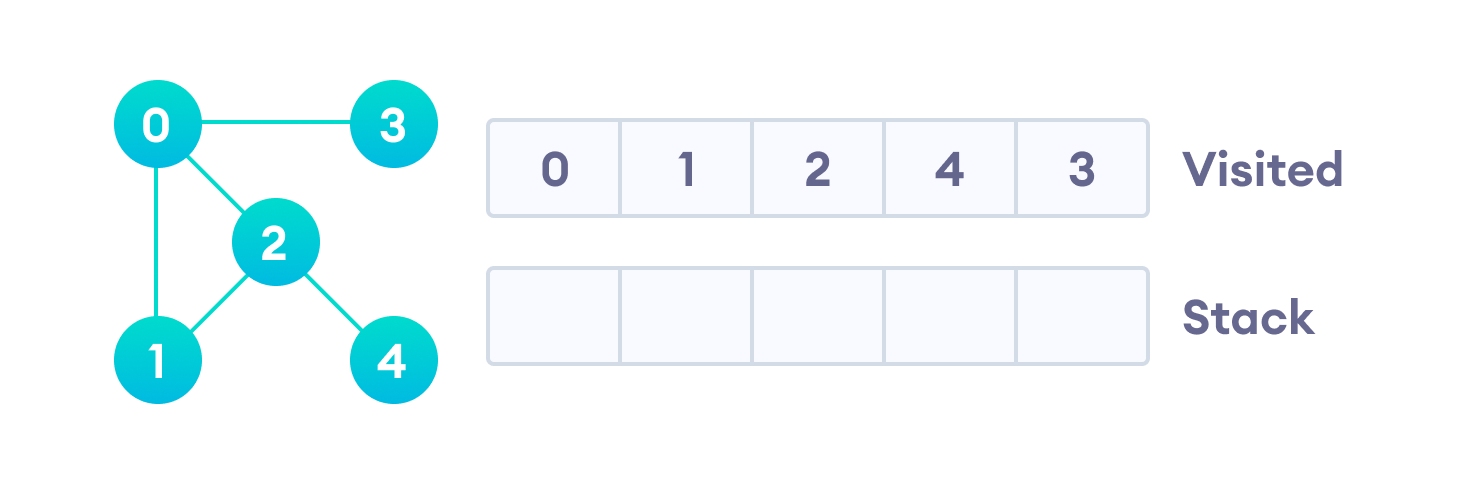
После того, как мы пройдем последний элемент (вершину “3”), в стеке не останется непройденных смежных вершин, и таким образом мы завершили обход графа в глубину.

Псевдокод поиска в глубину (рекурсивная реализация)

Ниже представлен псевдокод для алгоритма поиска в глубину. Обратите внимание, что в функции init() необходимо запускать функцию DFS на каждой вершине. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому для того, чтобы убедиться, что мы покрываем каждую вершину, мы должны запускать алгоритм поиска в глубину на каждой вершине.

DFS(G, u) u.visited = true for each v ∈ G.Adj[u] if v.visited == false DFS(G,v) init()

Реализация поиска в глубину на Python, Java и C/C++

Ниже приведены примеры реально кода алгоритма поиска в глубину. Код был упрощен, чтобы мы могли сфокусироваться на самом алгоритме, а не на других деталях.

# Алгоритм поиска в глубину на Python # Алгоритм def dfs(graph, start, visited=None): if visited is None: visited = set() visited.add(start) print(start) for next in graph[start] - visited: dfs(graph, next, visited) return visited graph = dfs(graph, '0')

// Алгоритм поиска в глубину на Java import java.util.*; class Graph < private LinkedListadjLists[]; private boolean visited[]; // Создание графа Graph(int vertices) < adjLists = new LinkedList[vertices]; visited = new boolean[vertices]; for (int i = 0; i < vertices; i++) adjLists[i] = new LinkedList(); > // Добавление ребер void addEdge(int src, int dest) < adjLists[src].add(dest); >// Алгоритм void DFS(int vertex) < visited[vertex] = true; System.out.print(vertex + " "); Iteratorite = adjLists[vertex].listIterator(); while (ite.hasNext()) < int adj = ite.next(); if (!visited[adj]) DFS(adj); >> public static void main(String args[]) < Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); System.out.println("Following is Depth First Traversal"); g.DFS(2); >> 

// Алгоритм поиска в глубину на C #include #include struct node < int vertex; struct node* next; >; struct node* createNode(int v); struct Graph < int numVertices; int* visited; // Нам нужен int** для хранения двумерного массива. // Аналогично, нам нужна структура node** для хранения массива связанных списков. struct node** adjLists; >; // Алгоритм void DFS(struct Graph* graph, int vertex) < struct node* adjList = graph->adjLists[vertex]; struct node* temp = adjList; graph->visited[vertex] = 1; printf("Visited %d \n", vertex); while (temp != NULL) < int connectedVertex = temp->vertex; if (graph->visited[connectedVertex] == 0) < DFS(graph, connectedVertex); >temp = temp->next; > > // Создание вершины struct node* createNode(int v) < struct node* newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; > // Создание графа struct Graph* createGraph(int vertices) < struct Graph* graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) < graph->adjLists[i] = NULL; graph->visited[i] = 0; > return graph; > // Добавление ребра void addEdge(struct Graph* graph, int src, int dest) < // Проводим ребро от начальной вершины ребра графа к конечной вершине ребра графа struct node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Проводим ребро из конечной вершины ребра графа в начальную вершину ребра графа newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; > // Выводим граф void printGraph(struct Graph* graph) < int v; for (v = 0; v < graph->numVertices; v++) < struct node* temp = graph->adjLists[v]; printf("\n Adjacency list of vertex %d\n ", v); while (temp) < printf("%d ->", temp->vertex); temp = temp->next; > printf("\n"); > > int main()

// Алгоритм прохода в глубину в C++ #include #include using namespace std; class Graph < int numVertices; list*adjLists; bool *visited; public: Graph(int V); void addEdge(int src, int dest); void DFS(int vertex); >; // Инициализация графа Graph::Graph(int vertices) < numVertices = vertices; adjLists = new list[vertices]; visited = new bool[vertices]; > // Добавление ребер void Graph::addEdge(int src, int dest) < adjLists[src].push_front(dest); >// Алгоритм void Graph::DFS(int vertex) < visited[vertex] = true; listadjList = adjLists[vertex]; cout << vertex << " "; list::iterator i; for (i = adjList.begin(); i != adjList.end(); ++i) if (!visited[*i]) DFS(*i); > int main()

Сложность алгоритма поиска в глубину

Временная сложность алгоритма поиска в глубину представлена ​​в виде O(V + E), где V — количество вершин, а E — количество ребер.

Пространственная сложность алгоритма равна O(V).

Применения алгоритма

1. Для поиска пути.
2. Для проверки двудольности графа.
3. Для поиска сильно связанных компонентов графа.
4. Для обнаружения циклов в графе.

Приглашаем всех желающих на открытый урок в OTUS «Теория графов. Термины и определения. Основные алгоритмы», регистрация доступна по ссылке.

Источник