Алгоритмы построения покрывающих деревьев

3 Покрывающие деревья (остовы)

Цикломатическим числом неориентированного графа G называется величина γ(G) = т — п + k, где т — число ребер, п — число вершин, k — число связных компонент. Для дерева и леса γ (G) = 0, для других графов γ (G) > 0.

Остовом, или покрывающим деревом, связного графа G=(V, E) называется часть G, которая содержит все его вершины и является деревом. Хордой остова графа G называется ребро G, не принадлежащее остову.

Очевидно, что любой связный граф имеет хотя бы один остов, а любой несвязный граф остова не имеет.

В последующем алгоритме части исходного графа G, которые возникают в процессе построения покрывающего дерева, будем называть букетами.

Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g

1. Выбрать любое ребро G, не являющееся петлей. Пометить его меткой α и объявить букетом это ребро вместе с его концевыми вершинами.

2. Выбрать любое непомеченное ребро G, не являющееся петлей:

а) если один из концов выбранного ребра принадлежит построенному ранее букету В, а другой конец свободен (не принадлежит ни одному букету), пометить выбранное ребро меткой α, включить его вместе со свободным концом в букет В и перейти к шагу 3;

б) если оба конца выбранного ребра свободны, поме­тить его меткой а, объявить это ребро вместе с его конце­выми вершинами новым букетом и перейти к шагу 3;

в) если концы выбранного ребра принадлежат разным построенным ранее букетам В и С, пометить выбранное ребро меткой α, включить его и букет С в букет В и перейти к шагу 3;

г) если оба конца выбранного ребра принадлежат одному букету, пометить его меткой β и перейти к шагу 3;

д) если непомеченных ребер нет, закончить алгоритм.

3. Если все вершины графа G вошли в один букет, закончить алгоритм. Если нет, перейти к шагу 2.

Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g

1. Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G₂ графа G. Положим i:=2.
2. Если i=n(G), то задача решена и G_i – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).
3. Строим граф G_i+1. Для этого добавим к графу G_i новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа G_i и одновременно вершине, не содержащейся в G_i. Вместе с этим ребром включаем в G_i+1 и эту инцидентную ему вершину. Присваиваем i:=i+1 и переходим к шагу 2.

Лекция 12 Двудольные и планарные графы

1 Двудольные графы

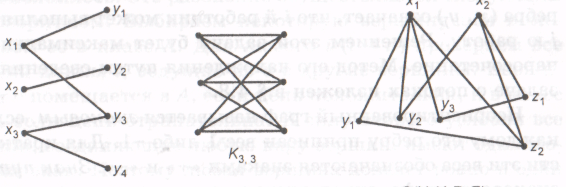
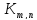
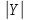
Двудольным графом G=(X, Y, Е) называется неориентированный граф, вершины которого можно разбить на два класса X и Y так, что концы каждого ребра принадлежат разным классам. Двудольный граф называется полным, если каждая вершина одной доли соединена с каждой вершиной другой доли, полный двудольный граф принято обозначать символом гдет = |Х|, n = . Введенные понятия допускают естественное обобще-ие. Неориентированный граф называется k-дольным, если его вершины можно разбить на k классов так, что концы каждого ребра принадлежат разным классам. Полный k-дольный граф — это k-дольный граф, в котором каждая вершина одной доли соединена с каждой вершиной всех остальных долей. Пример. На рисунке 24 представлены двудольный граф G=(X, Y, Е), полный двудольный граф К_3,3 и трехдольный граф G=(X, Y, Z, Е), где X = 1 x₂>, Y = 1 y₂, y₃>, Z = 1 z₂>. G=(X, Y, Е) G=(X, Y, Z, Е) Рисунок 24 – Двудольные графы Теорема. Граф является двудольным, если и только если длины всех его простых циклов четны. Паросочетанием в неориентированном графе называется множество попарно несмежных ребер. Задача о максимальном паросочетании заключается в нахождении паросочетания максимальной мощности. Для двудольного графа одной из наиболее известных интерпретаций задачи о максимальном паросочетании является задача о назначениях, которая заключается в следующем. Имеется т работников и п работ. Каждый работник способен выполнять несколько работ; каждую работу могут выполнять несколько работников. Требуется определить назначения по принципу «один работник — одна работа» так, чтобы загрузить максимальное число работников. Условия этой задачи представляются в виде двудольного графа, в котором вершины класса X соответствуют работникам, вершины класса Y- работам, а наличие ребра (x_i, y_j) означает, что i-й работник может выполнять j-ю работу. Решением этой задачи будет максимальное паросочетание, которое находится путем сведения к задаче о потоках.

Источник

Алгоритмы построения покрывающих деревьев

Рассмотрим граф G(X,E), в котором направление дуг не задаётся (т.е. это неориентированный граф). Предположим, что каждому ребру этого графа приписан вес . Определим вес покрывающего дерева, как сумму весов составляющих его рёбер.

В управлении шоссейных дорог рассматривается проект строительства новых дорог, которые должны связать пять городов некоторого района. Стоимость прокладки дороги между каждой парой городов известна.

Построим граф, вершины которого соответствуют городам, а рёбра – дорогам, которые могут быть проложены между определёнными городами. Каждому ребру приписан вес разной стоимости проекта строительства дороги.

Составление строительства дорог и городов теперь можно свести к задаче построения для графа покрывающего дерева минимальной стоимости.

Алгоритм можно представить как процесс окрашивания рёбер. При этом голубой цвет используется для окраски рёбер, включаемых при окраске дерева, а оранжевый – для окраски рёбер, не включаемых при окраске дерева.

При алгоритме окрашивания ребра осуществляется лишь проверка того, не образуется ли данное дерево в совокупности с уже включёнными рёбрами в дерево цикла.

Если результат проверки является положительным, то рассматриваемое ребро не включается в дерево, окрашивается в оранжевый цвет. В противном случае, ребро включается в дерево и окрашивается в голубой цвет.

Проверка на наличие цикла осуществляется так: проверяется, принадлежат ли обе концевые вершины одной и той же компоненты связности, которую ещё называют “букетом”. Работа алгоритма заканчивается, когда количество окрашенных рёбер в голубой цвет окажется на единицу меньше числа вершин или когда все вершины окажутся в одном букете.

Источник

Дискретка_Экзамен_Ответы / графы / 4 Покрывающие деревья минимальной стоимости, алгоритмы

Пусть задан граф со взвешенными рёбрами и его покрывающее дерево. Сумма весов рёбер, принадлежащих покрывающему дереву, называется стоимостью дерева. Покрывающее дерево графа, имеющее наименьшую стоимость по сравнению со всеми другими покрывающими деревьями этого же графа, называется покрывающим деревом минимальной стоимости.

Рассмотрим задачи, решение которых сводится к нахождению покрывающего дерева минимальной стоимости.

Задача 1. В управлении шоссейных дорог рассматривается проект строительства новых дорог, которые должны связать несколько городов некоторого района (причём не обязательно непосредственно каждую пару городов). Стоимость прокладки дороги между каждой парой городов известна. Необходимо определить, между какими городами нужно проложить дороги, чтобы суммарная стоимость прокладки дорог была минимальной.

Задача 2. Необходимо соединить проводами клеммы электрической сети, минимизируя длину проводника. Расстояния между каждой парой клемм известно.

Для нахождения покрывающего дерева минимальной стоимости можно получить все покрывающие деревья, определить их стоимость и выбрать дерево минимальной стоимости. Такой подход не является эффективным.

Алгоритм Краскала строит покрывающее дерево минимальной стоимости, если рёбра графа просматривать в порядке неубывания их весов. Поэтому для нахождения покрывающего дерева минимальной стоимости можно предварительно использовать алгоритм сортировки рёбер, а затем применить алгоритм Краскала. Тогда на каждом шаге будет выбираться ребро с минимальным весом, которое можно включить в покрывающее дерево. Такой выбор можно осуществить и в процессе выполнения алгоритма Краскала без предварительной сортировки рёбер. В этом случае при выборе ребра используем алгоритм нахождения ребра минимального веса среди рёбер, не включённых в дерево, при этом все рёбра, образующие цикл с рёбрами, включёнными в дерево, исключаются из дальнейшего рассмотрения.

Рассмотрим ещё один алгоритм построения покрывающего дерева минимальной стоимости, не требующий предварительной сортировки рёбер. Это алгоритм Прима (алгоритм ближайшего соседа). Он отличается от алгоритма Краскала тем, что в нём формируется только один букет. На очередном шаге выбирается ребро минимального веса среди рёбер, у которых одна концевая вершина принадлежит букету, а другая – не принадлежит. Такое ребро включается в дерево, а концевая вершина, не принадлежащая букету, включается в него.

Для эффективного выбора ребра в алгоритме Прима каждой вершине v_i графа, не принадлежащей букету Б приписывается метка t(v_i) – «ближайшая» к v_i вершина, принадлежащая букету Б, и число d(v_i) – вес ребра i),v_i>. На каждом шаге выполнения алгоритма вершина v_i с наименьшим числом d(v_i) добавляется к букету Б, а ребро i),v_i> – к покрывающему дереву. После добавления новой вершины v_i к букету Б метка t(v_j) и число d(v_j) вершины v_j, не принадлежащей букету, изменятся, если вес ребра i,v_j> меньше числа d(v_j)

Вход: G=(V,E) — взвешенный граф, где

V – множество вершин,

Выход: T – покрывающее дерево минимальной стоимости.

Каждой вершине v_i приписать t(v_i)=0;

Б:=v>, v –произвольная вершина графа включается в букет Б;

каждой вершине v_i, не принадлежащей букету, приписать d(v_i)= ,

y:=v, y – последняя вершина, включённая в букет;

T:=, дерево пусто.

2. Пересчёт чисел d(v_i) и меток t(v_i).

v_iГ(y)-Б пересчитать d(v_i):

Если число d(v_i) изменилась (уменьшилась), то t(v_i):=y.

3. Из всех вершин v_iБ выбрать вершину v_j с наименьшим числом d(v_j);

Б:=Бv_j>, включить выбранную вершину в букет;

y:=v_j, y – последняя вершина, включённая в букет;

T:=Tt(v_i),v_i>, добавить ребро в дерево.

4. Если все вершины графа включены в букет (Б=V), то конец алгоритма, иначе перейти к п.2

При программной реализации алгоритма Прима букет можно представить бинарным массивом Б, i-ый элемент которого соответствует вершине v_i и, если вершина v_i принадлежит букету, то Б_i=1, иначе Б_i=0. Числа d(v_i) целесообразно хранить в массиве D, i-ый элемент которого соответствует вершине v_i , а его значение D_i — числу d(v_i). Для хранения меток t(v_i) можно использовать массив T, i-ый элемент которого соответствует вершине v_i , а его значение T_i – метке t(v_i). Заметим, что массив T по окончании алгоритма хранит полную информацию о структуре построенного покрывающего дерева минимальной стоимости: пара T_i,i> соответствует ребру дерева, если T_i≠0, а сумма всех элементов массива D равна стоимости дерева.

Работу алгоритма Прима при построении покрывающего дерева минимальной стоимости графа, диаграмма которого изображена на рис.4.26, представим в таблице 4.4, отображающей изменения значений массивов Б, D и T на каждом шаге выполнения алгоритма.

v₁ v₆

5

Работа алгоритма Прима

Источник