Алгоритмы при помощи деревьев

Алгоритмы на деревьях

Пусть дан граф [math]G = \langle V, E \rangle [/math] . Тогда диаметром [math]d[/math] называется [math]\max\limits_ dist(v, u)[/math] , где [math]dist[/math] — кратчайшее расстояние между вершинами.

Алгоритм

• Возьмём любую вершину [math] v \in V [/math] и найдём расстояния до всех других вершин. [math]d[i] = dist(v, i)[/math]

• Возьмём вершину [math] u \in V [/math] такую, что [math]d[u] \geqslant d[t][/math] для любого [math]t[/math] . Снова найдём расстояние от [math]u[/math] до всех остальных вершин. Самое большое расстояние — диаметр дерева.

Расстояние до остальных вершин будем искать алгоритмом [math]BFS[/math] .

Реализация

//граф g представлен списком смежности int diameterTree(list> g): v = u = w = 0 d = bfs(g, v) for i = 0, i < n, i++ if d[i] > d[u] u = i d = bfs(g, u) for i = 0, i < n, i++ if d[i] > d[w] w = i return d[w]

Обоснование корректности

Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.

После запуска алгоритма получим дерево [math]BFS[/math] .

В дереве [math]BFS[/math] не существует ребер между вершинами из разных поддеревьев некоторого их общего предка.

Предположим, существует ребро [math]u, v[/math] между соседними поддеревьями:

Мы свели задачу к нахождению вершины [math]w[/math] , такой что сумма глубин поддеревьев максимальна.

Докажем, что одно из искомых поддеревьев содержит самый глубокий лист. Пусть нет, тогда, взяв расстояние от [math]w[/math] до глубочайшего листа, мы можем улучшить ответ.

Таким образом мы доказали, что нам нужно взять вершину [math]u[/math] с наибольшей глубиной после первого [math]BFS[/math] , очевидно, что ей в пару надо сопоставить вершину [math]w[/math] , такую что [math]dist(u, w)[/math] максимально. Вершину [math]w[/math] можно найти запуском [math]BFS[/math] из [math]u[/math] .

Оценка времени работы

Все операции кроме [math]BFS[/math] — [math]O(1)[/math] . [math]BFS[/math] работает за линейное время, запускаем мы его два раза. Получаем [math]O(|V| + |E|)[/math] .

Центр дерева

Определения

Определение:

Эксцентриситет вершины [math]e(v)[/math] (англ. eccentricity of a vertex) — [math]\max\limits_ dist(v, u)[/math] , где [math]V[/math] — множество вершин связного графа [math]G[/math] .

Определение:

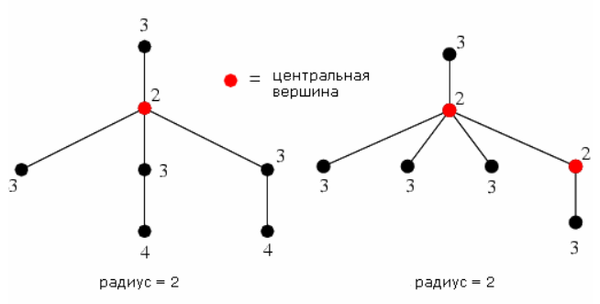
Радиус [math]r(G)[/math] (англ. radius) — наименьший из эксцентриситетов вершин графа [math]G[/math] .

Определение:

Центральная вершина (англ. central vertex) — вершина графа [math]G[/math] , такая что [math]e(v) = r(G)[/math]

Определение:

Центр графа [math]G[/math] (англ. center of a graph) — множество всех центральных вершин графа [math]G[/math] .

Алгоритм

Наивный алгоритм

Найдём центр графа исходя из его определения.

• Построим матрицу [math]A_[/math] ( [math]n[/math] — мощность множества [math]V[/math] ), где [math]a_ = d_[/math] , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
• Подсчитаем максимум в каждой строчке матрицы [math]A[/math] . Таким образом, получим массив длины [math]n[/math] .
• Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.

Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет [math]O(V^3)[/math] , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и [math]O(V^2)[/math] , за которую мы находим максимумы в матрице.

Алгоритм для дерева за O(n)

Собственно, алгоритм нахождения центра описан в доказательстве теоремы.

• Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом [math]0[/math] .
• Обрежем помеченные вершины.
• Образовавшиеся листья пометим числом [math]1[/math] и тоже обрежем.
• Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.

Оставшиеся листья являются центром дерева.

Для того, чтобы алгоритм работал за [math]O(n)[/math] , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.

См. также

Источники информации

Источник

Классификация и регрессия с помощью деревьев принятия решений

В данной статье сделан обзор деревьев принятия решений (Decision trees) и трех основных алгоритмов, использующих эти деревья для построение классификационных и регрессионных моделей. В свою очередь будет показано, как деревья принятия решения, изначально ориентированные на классификацию, используются для регрессии.

Деревья принятия решений

Дерево принятия решений — это дерево, в листьях которого стоят значения целевой функции, а в остальных узлах — условия перехода (к примеру “ПОЛ есть МУЖСКОЙ”), определяющие по какому из ребер идти. Если для данного наблюдения условие истина то осуществляется переход по левому ребру, если же ложь — по правому.

Классификация

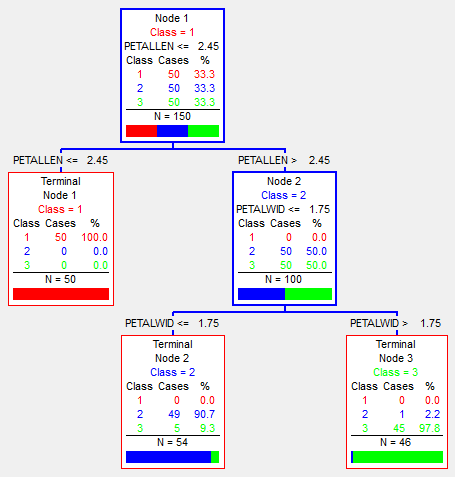
На изображении приведенном выше показано дерево классификации ирисов. Классификация идет на три класса (на изображении помечены — красным, синим и зеленым), и проходит по параметрам: длина\толщина чашелистика (SepalLen, SepalWid) и длина\толщина лепестка (PetalLen, PetalWid). Как видим, в каждом узле стоит его принадлежность к классу (в зависимости от того, каких элементов больше попало в этот узел), количество попавших туда наблюдений N, а так же количество каждого класса. Так же не в листовых вершинах есть условие перехода — в одну из дочерних. Соответственно, по этим условиям и разбивается выборка. В результате, это дерево почти идеально (6 из 150 неправильно) классифицировало исходные данные (именно исходные — те на которых оно обучалось).

Регрессия

Если при классификации в листах стоят результирующие классы, при регрессии же стоит какое-то значение целевой функции.

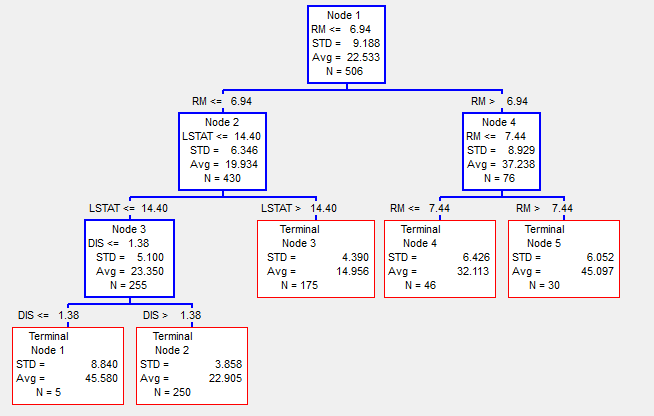
На выше приведенном изображении регрессионное дерево, для определения цены на землю в городе Бостон в 1978 году, в зависимости от параметров RM — количество комнат, LSTAT — процент неимущих и нескольких других параметров (более детально можно посмотреть в [4]). Соответственно, здесь в каждом узле мы видим среднее значение (Avg) и стандартное отклонение (STD) значений целевой функции наблюдений попавших в эту вершину. Общее количество наблюдений попавших в узел N. Результатом регрессии будет то значение среднего (Avg), в какой узел попадёт наблюдение.
Таким образом изначально классификационное дерево, может работать и для регрессии. Однако при таком подходе, обычно требуются большие размеры дерева, чем при классификации, что бы достигнуть хороших результатов регрессии.

Основные методы

Ниже перечислены несколько основных методов, которые используют деревья принятия решений. Их краткое описание, плюсы и минусы.

CART

CART (англ. Classification and regression trees — Классификационные и регрессионные деревья) был первым из методов, придуманный в 1983 четверкой известных ученых в области анализа данных: Leo Breiman, Jerome Friedman, Richard Olshen and Stone [1].
Суть этого алгоритма состоит в обычном построении дерева принятия решений, не больше и не меньше.
На первой итерации мы строим все возможные (в дискретном смысле) гиперплоскости, которые разбивали бы наше пространство на два. Для каждого такого разбиения пространства считается количество наблюдений в каждом из подпространств разных классов. В результате выбирается такое разбиение, которое максимально выделило в одном из подпространств наблюдения одного из классов. Соответственно, это разбиение будет нашим корнем дерева принятия решений, а листами на данной итерации будет два разбиения.
На следующих итерациях мы берем один худший (в смысле отношения количества наблюдений разных классов) лист и проводим ту же операцию по разбиению его. В результате этот лист становится узлом с каким-то разбиением, и двумя листами.
Продолжаем так делать, пока не достигнем ограничения по количеству узлов, либо от одной итерации к другой перестанет улучшаться общая ошибка (количество неправильно классифицированных наблюдений всем деревом). Однако, полученное дерево будет “переобучено” (будет подогнано под обучающую выборку) и, соответственно, не будет давать нормальные результаты на других данных. Для того, что бы избежать “переобучения”, используют тестовые выборки (либо кросс-валидацию) и, соответственно, проводится обратный анализ (так называемый pruning), когда дерево уменьшают в зависимости от результата на тестовой выборке.
Относительно простой алгоритм, в результате которого получается одно дерево принятия решений. За счет этого, он удобен для первичного анализа данных, к примеру, что бы проверить на наличие связей между переменными и другим.
Быстрое построение модели
Легко интерпретируется (из-за простоты модели, можно легко отобразить дерево и проследить за всеми узлами дерева)
Часто сходится на локальном решении (к примеру, на первом шаге была выбрана гиперплоскость, которая максимально делит пространство на этом шаге, но при этом это не приведёт к оптимальному решению)

RandomForest

Random forest (Случайный лес) — метод, придуманный после CART одним из четверки — Leo Breiman в соавторстве с Adele Cutler [2], в основе которого лежит использование комитета (ансамбля) деревьев принятия решений.
Суть алгоритма, что на каждой итерации делается случайная выборка переменных, после чего, на этой новой выборке запускают построение дерева принятия решений. При этом производится “bagging” — выборка случайных двух третей наблюдений для обучения, а оставшаяся треть используется для оценки результата. Такую операцию проделывают сотни или тысячи раз. Результирующая модель будет будет результатом “голосования” набора полученных при моделировании деревьев.
Высокое качество результата, особенно для данных с большим количеством переменных и малым количеством наблюдений.
Возможность распараллелить
Не требуется тестовая выборка
Каждое из деревьев огромное, в результате модель получается огромная
Долгое построение модели, для достижения хороших результатов.
Сложная интерпретация модели (Сотни или тысячи больших деревьев сложны для интерпретации)

Stochastic Gradient Boosting

Stochastic Gradient Boosting (Стохастическое градиентное добавление) — метод анализа данных, представленный Jerome Friedman [3] в 1999 году, и представляющий собой решение задачи регрессии (к которой можно свести классификацию) методом построения комитета (ансамбля) “слабых” предсказывающих деревьев принятия решений.
На первой итерации строится ограниченное по количеству узлов дерево принятия решений. После чего считается разность между тем, что предсказало полученное дерево умноженное на learnrate (коэффициент “слабости” каждого дерева) и искомой переменной на этом шаге.
Yi+1=Yi-Yi*learnrate
И уже по этой разнице строится следующая итерация. Так продолжается, пока результат не перестанет улучшаться. Т.е. на каждом шаге мы пытаемся исправить ошибки предыдущего дерева. Однако здесь лучше использовать проверочные данные (не участвовавшие в моделировании), так как на обучающих данных возможно переобучение.
Высокое качество результата, особенно для данных с большим количеством наблюдений и малым количеством переменных.
Сравнительно (с предыдущим методом) малый размер модели, так как каждое дерево ограничено заданными размерами.
Сравнительно (с предыдущим методом) быстрое время построение оптимальное модели
Требуется тестовая выборка (либо кросс-валидация)
Невозможность хорошо распараллелить
Относительно слабая устойчивость к ошибочным данным и переобучению
Сложная интерпретация модели (Так же как и в Random forest)

Заключение

Список литературы

1. “Classification and Regression Trees”. Breiman L., Friedman J. H., Olshen R. A, Stone C. J.
2. “Random Forests”. Breiman L.
3. “Stochastic Gradient Boosting”. Friedman J. H.
4. http://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html

Источник