Альтернативы дерева принятия решений

Альтернативное дерево решений — Alternating decision tree

Дерево альтернативных решений (ADTree) — это метод машинного обучения для классификации. Он обобщает деревья решений и имеет связи с повышением.

. ADTree состоит из чередования узлов решений, которые задают условие предиката, и узлов прогнозирования, которые содержат одно число. Экземпляр классифицируется с помощью ADTree, следуя всем путям, для которых все узлы решения истинны, и суммируя все пройденные узлы прогнозирования.

• 1 История
• 2 Мотивация
• 3 Древовидная структура альтернативных решений
  • 3.1 Пример

  История

  ADTrees были представлены Йоавом Фройндом и Лью Мэйсоном. Однако представленный алгоритм содержал несколько типографских ошибок. Разъяснения и оптимизации были позже представлены Бернхардом Пфарингером, Джеффри Холмсом и Ричардом Киркби. Реализации доступны в Weka и JBoost.

  Мотивация

  Исходные алгоритмы повышения обычно использовали либо пни принятия решений, либо деревья решений в качестве слабых гипотез. Например, при повышении точек принятия решения создается набор T взвешенных точек принятия решения (где T — количество итераций повышения), которые затем голосуют за окончательную классификацию в соответствии с их весами. Отдельные этапы принятия решения взвешиваются в зависимости от их способности классифицировать данные.

  Повышение уровня простого ученика приводит к неструктурированному набору гипотез T , что затрудняет вывод корреляций между атрибутами. Чередующиеся деревья решений привносят структуру в набор гипотез, требуя, чтобы они основывались на гипотезе, выдвинутой на более ранней итерации. Результирующий набор гипотез можно визуализировать в виде дерева на основе взаимосвязи между гипотезой и ее «родителем».

  Другой важной особенностью алгоритмов с усилением является то, что данным дается различное распределение на каждой итерации. Экземплярам, ​​которые неправильно классифицированы, присваивается больший вес, а точно классифицированным экземплярам — уменьшенный вес.

  Структура дерева альтернативных решений

  Дерево альтернативных решений состоит из узлов решений и узлов прогнозирования. Узлы принятия решений определяют условие предиката. Узлы прогноза содержат одно число. ADTrees всегда имеют узлы прогнозирования как корневые, так и конечные. Экземпляр классифицируется ADTree, следуя всем путям, для которых все узлы решения истинны, и суммируя все пройденные узлы прогнозирования. Это отличается от бинарных деревьев классификации, таких как CART (Дерево классификации и регрессии ) или C4.5, в которых экземпляр следует только по одному пути через дерево.

  Пример

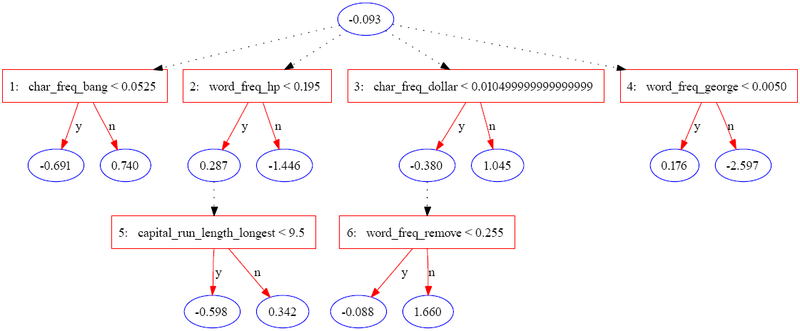
  Следующее дерево было построено с использованием JBoost в наборе данных спамба (доступно в репозитории машинного обучения UCI). В этом примере спам кодируется как 1, а обычная электронная почта — как -1.

  

  В следующей таблице содержится часть информации для одного экземпляра.

  Классифицируемый экземпляр

  Feature	Значение
  char_freq_bang	0,08
  word_freq_hp	0,4 ​​
  capital_run_length_longest	4
  char_freq_dollar	0
  word_freq_remove	0.9
  word_freq_george	0
  Другие функции	.

  Экземпляр оценивается путем суммирования всех узлов прогнозирования, через которые он проходит. В случае приведенного выше примера оценка рассчитывается как

  Основным элементом алгоритма ADTree является правило. Одно правило состоит из предварительного условия, условия и двух оценок. Условие — это предикат формы «значение атрибута ». Предусловие — это просто логическое соединение условий. Оценка правила включает пару вложенных операторов if:

  1 if(предварительное условие) 2 if (условие) 3 return score_one 4 else 5 return score_two 6 end if 7 else 8 return 0 9 end if

  Алгоритм также требует нескольких вспомогательных функций:

  • W + (c) (c)> возвращает сумму весов всех положительно помеченных примеров, которые удовлетворяют предикату c
  • W — (c) (c)> возвращает сумму весов всех отрицательно помеченных примеров, которые удовлетворяют предикату c
  • W (c) = W + (c) + W — (c) (c) + W _ (c)> возвращает сумму веса всех примеров, удовлетворяющих предикату c

  Алгоритм выглядит следующим образом:

  1 function ad_tree 2 input Набор из m обучающих экземпляров 3 4 w i = 1 / m для всех i 5 $a\; =\; 1\; 2\; ln\; W\; +\; (true)\; W\; -\; (true)\; >\; >\; (true)>\; (true)>>>$ 6 R 0 = правило с оценками а и 0, предварительным условием «истина» и условием «истина». 7 $P\; =\; >\; =\; \backslash \; >$ 8 $C\; =\; >\; =>$ набор всех возможных условий 9 для$j\; =\; 1\dots \; T$10 $p\; \in \; P,\; c\; \in \; C\; >,\; c\; \backslash \; in\; >>$получить значения, которые минимизируют $z\; =\; 2\; (W\; +\; (p\; \wedge \; c)\; W\; -\; (\; п\; \wedge \; с)\; +\; W\; +\; (п\; \wedge \; \neg \; c)\; W\; -\; (п\; \wedge \; \neg \; c))\; +\; W\; (\neg \; p)\; (p\; \backslash \; wedge\; c)\; W\; \_\; (p\; \backslash \; wedge\; c)>>\; +\; (p\; \backslash \; wedge\; \backslash \; neg\; c)\; W\; \_\; (p\; \backslash \; wedge\; \backslash \; neg\; c)>>\; \backslash \; right)\; +\; W\; (\; \backslash \; neg\; p)>$ 11 $P\; +\; =\; p\; \wedge \; c\; +\; p\; \wedge \; \neg \; c\; >\; +\; =\; p\; \backslash \; wedge\; c\; +\; p\; \backslash \; wedge\; \backslash \; neg\; c>$ 12 $a\; 1\; =\; 1\; 2\; ln\; W\; +\; (p\; \wedge \; c)\; +\; 1\; W\; -\; (p\; \wedge \; c)\; +\; 1\; =\; >\; >\; (p\; \backslash \; wedge\; c)\; +1>\; (p\; \backslash \; wedge\; c)\; +1>>>$ 13  14 R j = новое правило с предусловием p, условием c и весами a 1 и a 2 15  16 конец для 17 return набор R j

  Набор P >> увеличивается на два предварительных условия в каждой итерации, и можно получить древовидная структура набора правил с указанием предусловия, которое используется в каждом последующем правиле.

  Эмпирические результаты

  Рисунок 6 в исходной статье демонстрирует, что ADTrees обычно столь же устойчивы, как усиленные деревья решений и увеличенные пни принятия решений. Как правило, эквивалентной точности можно добиться с помощью гораздо более простой древовидной структуры, чем алгоритмы рекурсивного разделения.

  Ссылки

  Внешние ссылки

  • Введение в Boosting и ADTrees (содержит множество графических примеров чередующихся деревьев решений на практике).
  • Программное обеспечение JBoost, реализующее ADTrees.

  Источник