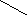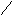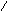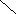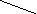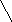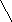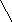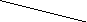Арифметические выражения бинарные дерева

4.4.4. Представление выражений с помощью деревьев

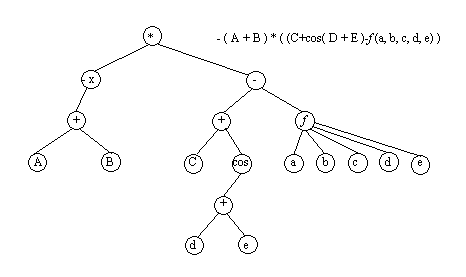
С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу операция. В общем случае дерево при этом может оказаться не бинарным.

Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным.

Рис.4.16. Представление арифметического выражения произвольного вида в виде дерева.

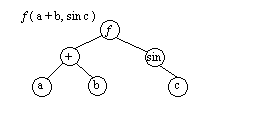
Рис. 4.17. Представление арифметического выражения в виде бинарного дерева

Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.

Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения.

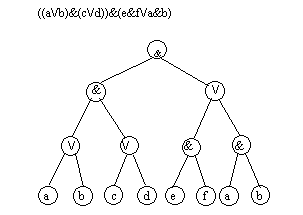
Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным

Рис.4.18. Вычисление арифметического выражения с помощью бинарного дерева

Рис. 4.19. Представление логического выражения в виде бинарного дерева

4.5. Представление сильноветвящихся деревьев

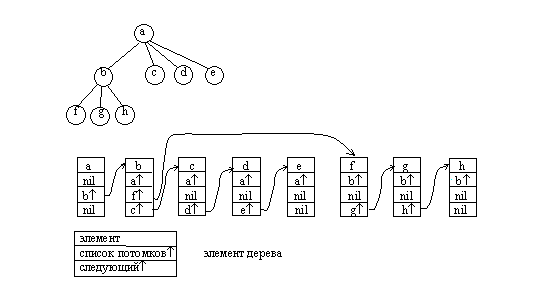
До сих пор мы рассматривали только способы представления бинарных деревьев. В ряде задач используются сильноветвящиеся деревья. Каждый элемент для представления бинарного дерева должен содержать как минимум три поля значение или имя узла, указатель левого поддерева, указатель правого поддерева. Произвольные деревья могут быть бинарными или сильноветвящимися. Причем число потомков различных узлов не ограничено и заранее не известно.

Тем не менее, для представления таких деревьев достаточно иметь элементы, аналогичные элементам списковой структуры бинарного дерева. Элемент такой структуры содержит минимум три поля: значение узла, указатель на начало списка потомков узла, указатель на следующий элемент в списке потомков текущего уровня. Также как и для бинарного дерева необходимо хранить указатель на корень дерева. При этом дерево представлено в виде структуры, связывающей списки потомков различных вершин. Такой способ представления вполне пригоден и для бинарных деревьев.

Представление деревьев с произвольной структурой в виде массивов может быть основано на матричных способах представления графов.

Рис.4.20. Представление сильноветвящихся деревьев в виде списков

4.6. Применение сильноветвящихся деревьев

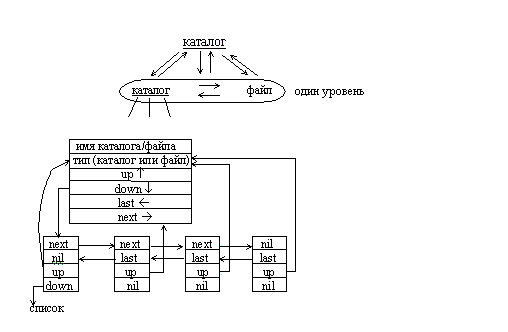
Один из примеров применения сильноветвящихся деревьев был связан с представлением арифметических выражений произвольного вида. Рассмотрим использование таких деревьев для представления иерархической структуры каталогов файловой системы. Во многих файловых системах структура каталогов и файлов, как правило, представляет собой одно или несколько сильноветвящихся деревьев. В файловой системе MS Dos корень дерева соответствует логическому диску. Листья дерева соответствуют файлам и пустым каталогам, а узлы с ненулевой степенью — непустым каталогам.

Рис.4.21. Представление логической структуры каталогов и файлов в виде сильноветвящегося дерева.

Для представления такой структуры используем расширение спискового представления сильноветвящихся деревьев. Способы представления деревьев, рассмотренные ранее, являются предельно экономичными, но не очень удобными для перемещения по дереву в разных направлениях. Именно такая задача встает при просмотре структуры каталогов. Необходимо осуществлять ⌠навигацию■ перемещаться из текущего каталога в каталог верхнего или нижнего уровня, или от файла к файлу в пределах одного каталога.

Для облегчения этой задачи сделаем списки потомков двунаправленными. Для этого достаточно ввести дополнительный указатель на предыдущий узел ■last■. С целью упрощения перемещения по дереву от листьев к корню введем дополнительный указатель на предок текущего узла ⌠up■. Общими с традиционными способами представления являются указатели на список потомков узла ⌠down■ и следующий узел ⌠next■.

Для представления оглавления диска служат поля имя и тип файла/каталога. Рассмотрим программу, которая осуществляет чтение структуры заданного каталога или диска, позволяет осуществлять навигацию и подсчет места занимаемого любым каталогом.

Источник

7.4.4. Представление выражений с помощью деревьев

С помощью деревьев можно представлять произвольные арифметические выражения (рис. 7.22-7.23). Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу – операция. В общем случае дерево при этом может оказаться не бинарным. Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным. -(A+B)*((C+cos(D+E)-f(a,b,c,d,e))Рис. 7.22. Представление арифметического выражения произвольного вида в виде дерева. f(a+b,sin c)Рис. 7.23. Представление арифметического выражения в виде бинарного дерева. Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления (рис. 7.24). В листьях записываются значения операндов. Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения. (1+10)*5 Рис. 7.24. Вычисление арифметического выражения с помощью бинарного дерева. Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов, например, логические выражения (рис. 7.25). Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным. ((aVb)&(cVd))&(e&fVa&b)Рис. 7.25. Представление логического выражения в виде бинарного дерева.

7.5. Представление сильноветвящихся деревьев

Произвольные деревья могут быть сильноветвящимися. Причем число потомков различных узлов не ограничено и заранее не известно. Тем не менее, для представления таких деревьев достаточно иметь элементы, аналогичные элементам списковой структуры бинарного дерева. Элемент такой структуры содержит минимум три поля: значение узла, указатель на начало списка потомков узла, указатель на следующий элемент в списке потомков текущего уровня. Также как и для бинарного дерева необходимо хранить указатель на корень дерева. При этом дерево представлено в виде структуры, связывающей списки потомков различных вершин. Такой способ представления вполне пригоден и для бинарных деревьев. Представление деревьев с произвольной структурой в виде массивов может быть основано на матричных способах представления графов. Рассмотрим использование сильноветвящихся деревьев для представления иерархической структуры каталогов файловой системы. Во многих файловых системах структура каталогов и файлов, как правило, представляет одно или несколько сильноветвящихся деревьев. В файловой системе корень дерева соответствует логическому диску. Листья дерева соответствуют файлам и пустым каталогам, а узлы с ненулевой степенью – непустым каталогам. Для представления такой структуры используем расширение спискового представления сильноветвящихся деревьев (рис. 7.26). Способы представления деревьев, рассмотренные ранее, являются предельно экономичными, но не очень удобными для перемещения по дереву в разных направлениях. Именно такая задача встает при просмотре структуры каталогов. Необходимо осуществлять навигацию – перемещаться из текущего каталога в каталог верхнего или нижнего уровня, или от файла к файлу в пределах одного каталога. Списки потомков можно сделать двунаправленными. Для этого необходимо ввести указатель на предыдущий узел last, а для упрощения перемещения по дереву от листьев к корню потребуется указатель на предок текущего узла up. Общими с традиционными способами представления являются указатели на список потомков узла down и следующий узел next. a nil b nil b a f c c a nil d d a nil e e a nil nil f b nil g g b nil h h b nil nil элемент список потомков следующий элемент дерева Рис. 7.26. Представление сильноветвящихся деревьев в виде списков.

Источник