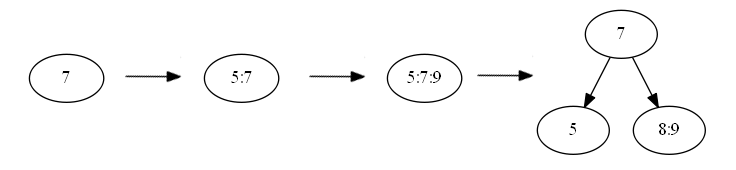
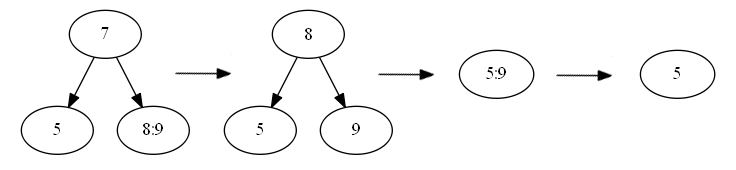
Сбалансированное дерево поиска B-tree (t=2)
На 3-м курсе обучения в своем университете передо мной встала задача реализовать B-дерево, содержащее уникальные ключи, упорядоченное по возрастанию (со степенью t=2) на языке c++ (с возможностью добавления, удаления, поиска элементов и соответственно, перестройкой дерева).
Перечитав несколько статей на Хабре (например, B-tree, 2-3-дерево. Наивная реализация и другие), казалось бы, все было ясно. Только теоретически, а не практически. Но и с этими трудностями мне удалось справиться. Цель моего поста — поделиться полученным опытом с пользователями.
Немного основных моментов
B-деревом называется дерево, удовлетворяющее следующим свойствам:
1. Каждый узел содержит хотя бы один ключ. Корень содержит от 1 до 2t-1 ключей. Любой другой узел содержит от t-1 до 2t-1 ключей. Листья не являются исключением из этого правила. Здесь t — параметр дерева, не меньший 2.
2. У листьев потомков нет. Любой другой узел, содержащий n ключей, содержит n+1 потомков. При этом:
а) Первый потомок и все его потомки содержат ключи из интервала ;
б) Для , i-й потомок и все его потомки содержат ключи из интервала ;
в) (n+1)-й потомок и все его потомки содержат ключи из интервала .
3. Глубина всех листьев одинакова.
Реализация
const int t=2; struct BNode < int keys[2*t]; BNode *children[2*t+1]; BNode *parent; int count; //количество ключей int countSons; //количество сыновей bool leaf; >;Теперь создадим класс Tree, включающий в себя соответствующие методы.
Сразу описываем конструктор и деструктор. В деструкторе вызывается рекурсивный метод удаления элементов из дерева.
Tree::Tree() < root=nullptr; >Tree::~Tree() < if(root!=nullptr) deletenode(root); >void Tree::deletenode(BNode *node)< if (node!=nullptr)< for (int i=0; ichildren[i]!=nullptr) deletenode(node->children[i]); else < delete(node); break; >> > >Первым делом рассмотрим добавление ключа в узел. В моем случае (t=2) это будет выглядеть следующим образом:
Т.е., как только в узле становится больше 3 элементов — узел разбивается.
Итак, для добавления элемента в дерево необходимо реализовать несколько методов.
Первый – простое добавление в узел. В данном методе вызывается метод сортировки, необходимый для выполнения условия о возрастающих значениях дерева. Второй метод –
добавления значения в узел, в котором предварительно ищется нужная позиция и при
необходимости (в узле становится больше 3 элементов) вызывается третий метод – метод разбиения узла на: родителя и двух сыновей.
Первый метод – метод простого добавления.
void Tree::insert_to_node(int key, BNode *node)< node->keys[node->count]=key; node->count=node->count+1; sort(node); >Метод сортировки чисел в узле:
void Tree::sort(BNode *node) < int m; for (int i=0; ikeys[i]!=0) && (node->keys[j]!=0))< if ((node->keys[i]) > (node->keys[j]))< m=node->keys[i]; node->keys[i]=node->keys[j]; node->keys[j]=m; > > else break; > > >Второй метод – метод добавления значения в узел с предварительным поиском позиции:
void Tree::insert(int key)< if (root==nullptr) < BNode *newRoot = new BNode; newRoot->keys[0]=key; for(int j=1; jkeys[j]=0; for (int i=0; ichildren[i]=nullptr; newRoot->count=1; newRoot->countSons=0; newRoot->leaf=true; newRoot->parent=nullptr; root=newRoot; > else < BNode *ptr=root; while (ptr->leaf==false)< //выбор ребенка до тех пор, пока узел не будет являться листом for (int i=0; ikeys[i]!=0) < if (keykeys[i]) < ptr=ptr->children[i]; break; > if ((ptr->keys[i+1]==0)&&(key>ptr->keys[i])) < ptr=ptr->children[i+1]; //перенаправляем к самому последнему ребенку, если цикл не "сломался" break; > > else break; > > insert_to_node(key, ptr); while (ptr->count==2*t) < if (ptr==root)< restruct(ptr); break; >else < restruct(ptr); ptr=ptr->parent; > > > >Третий метод – метод разбиения узла:
void Tree::restruct(BNode *node)< if (node->count<(2*t-1)) return; //первый сын BNode *child1 = new BNode; int j; for (j=0; j<=t-2; j++) child1->keys[j]=node->keys[j]; for (j=t-1; jkeys[j]=0; child1->count=t-1; //количество ключей в узле if(node->countSons!=0)< for (int i=0; ichildren[i]=node->children[i]; child1->children[i]->parent=child1; > for (int i=t; ichildren[i]=nullptr; child1->leaf=false; child1->countSons=t-1; //количество сыновей > else < child1->leaf=true; child1->countSons=0; for (int i=0; ichildren[i]=nullptr; > //второй сын BNode *child2 = new BNode; for (int j=0; jkeys[j]=node->keys[j+t]; for (j=t; jkeys[j]=0; child2->count=t; //количество ключей в узле if(node->countSons!=0) < for (int i=0; ichildren[i]=node->children[i+t]; child2->children[i]->parent=child2; > for (int i=t+1; ichildren[i]=nullptr; child2->leaf=false; child2->countSons=t; //количество сыновей > else < child2->leaf=true; child2->countSons=0; for (int i=0; ichildren[i]=nullptr; > //родитель if (node->parent==nullptr)< //если родителя нет, то это корень node->keys[0]=node->keys[t-1]; for(int j=1; jkeys[j]=0; node->children[0]=child1; node->children[1]=child2; for(int i=2; ichildren[i]=nullptr; node->parent=nullptr; node->leaf=false; node->count=1; node->countSons=2; child1->parent=node; child2->parent=node; > else < insert_to_node(node->keys[t-1], node->parent); for (int i=0; iparent->children[i]==node) node->parent->children[i]=nullptr; > for (int i=0; iparent->children[i]==nullptr) < for (int j=(2*t); j>(i+1); j--) node->parent->children[j]=node->parent->children[j-1]; node->parent->children[i+1]=child2; node->parent->children[i]=child1; break; > > child1->parent=node->parent; child2->parent=node->parent; node->parent->leaf=false; delete node; > >Для поиска были реализованы следующие методы, возвращающие true или false (второй метод рекурсивный):
bool Tree::search(int key)< return searchKey(key, this->root); > bool Tree::searchKey(int key, BNode *node)< if (node!=nullptr)< if (node->leaf==false)< int i; for (i=0; ikeys[i]!=0) < if(key==node->keys[i]) return true; if ((keykeys[i]))< return searchKey(key, node->children[i]); break; > > else break; > return searchKey(key, node->children[i]); > else < for(int j=0; jkeys[j]) return true; return false; > > else return false; >Реализация метода удаления ключа из узла была самой сложной. Ведь в некоторых случаях удаления нужно склеивать соседние узлы, а в некоторых брать значения из узлов «братьев». Например:
Удаление представляет собой несколько случаев. Первый из них — простой метод удаления ключа из узла:
void Tree::removeFromNode(int key, BNode *node)< for (int i=0; icount; i++)< if (node->keys[i]==key)< for (int j=i; jcount; j++) < node->keys[j]=node->keys[j+1]; node->children[j]=node->children[j+1]; > node->keys[node->count-1]=0; node->children[node->count-1]=node->children[node->count]; node->children[node->count]=nullptr; break; > > node->count--; >Во втором же случае после удаления ключа необходимо соединить соседние узлы. Поэтому второй и третий методы – методы соединения узлов:
void Tree::lconnect(BNode *node, BNode *othernode)< if (node==nullptr) return; for (int i=0; i<=(othernode->count-1); i++)< node->keys[node->count]=othernode->keys[i]; node->children[node->count]=othernode->children[i]; node->count=node->count+1; > node->children[node->count]=othernode->children[othernode->count]; for (int j=0; jcount; j++)< if (node->children[j]==nullptr) break; node->children[j]->parent=node; > delete othernode; > void Tree::rconnect(BNode *node, BNode *othernode)< if (node==nullptr) return; for (int i=0; i<=(othernode->count-1); i++)< node->keys[node->count]=othernode->keys[i]; node->children[node->count+1]=othernode->children[i+1]; node->count=node->count+1; > for (int j=0; jcount; j++)< if (node->children[j]==nullptr) break; node->children[j]->parent=node; > delete othernode; >Четвертый метод – метод «починки» узла. В данном методе дерево в буквальном смысле перестраивается до тех пор, пока не будут удовлетворены все условия B-дерева:
void Tree::repair(BNode *node)< if ((node==root)&&(node->count==0))< if (root->children[0]!=nullptr)< root->children[0]->parent=nullptr; root=root->children[0]; > else < delete root; >return; > BNode *ptr=node; int k1; int k2; int positionSon; BNode *parent=ptr->parent; for (int j=0; jcount; j++)< if (parent->children[j]==ptr) < positionSon=j; //позиция узла по отношению к родителю break; >> //если ptr-первый ребенок (самый левый) if (positionSon==0)< insert_to_node(parent->keys[positionSon], ptr); lconnect(ptr, parent->children[positionSon+1]); parent->children[positionSon+1]=ptr; parent->children[positionSon]=nullptr; removeFromNode(parent->keys[positionSon], parent); if(ptr->count==2*t)< while (ptr->count==2*t) < if (ptr==root)< restruct(ptr); break; >else < restruct(ptr); ptr=ptr->parent; > > > else if (parent->count <=(t-2)) repair(parent); >else < //если ptr-последний ребенок (самый правый) if (positionSon==parent->count)< insert_to_node(parent->keys[positionSon-1], parent->children[positionSon-1]); lconnect(parent->children[positionSon-1], ptr); parent->children[positionSon]=parent->children[positionSon-1]; parent->children[positionSon-1]=nullptr; removeFromNode(parent->keys[positionSon-1], parent); BNode *temp=parent->children[positionSon]; if(ptr->count==2*t)< while (temp->count==2*t) < if (temp==root)< restruct(temp); break; >else < restruct(temp); temp=temp->parent; > > > else if (parent->count <=(t-2)) repair(parent); >else < //если ptr имеет братьев справа и слева insert_to_node(parent->keys[positionSon], ptr); lconnect(ptr, parent->children[positionSon+1]); parent->children[positionSon+1]=ptr; parent->children[positionSon]=nullptr; removeFromNode(parent->keys[positionSon], parent); if(ptr->count==2*t)< while (ptr->count==2*t) < if (ptr==root)< restruct(ptr); break; >else < restruct(ptr); ptr=ptr->parent; > > > else if (parent->count <=(t-2)) repair(parent); >> >Пятый метод – метод удаления ключа из листа:
void Tree::removeLeaf(int key, BNode *node)< if ((node==root)&&(node->count==1))< removeFromNode(key, node); root->children[0]=nullptr; delete root; root=nullptr; return; > if (node==root) < removeFromNode(key, node); return; >if (node->count>(t-1)) < removeFromNode(key, node); return; >BNode *ptr=node; int k1; int k2; int position; int positionSon; int i; for (int i=0; icount-1; i++)< if (key==node->keys[i]) < position=i; //позиция ключа в узле break; >> BNode *parent=ptr->parent; for (int j=0; jcount; j++)< if (parent->children[j]==ptr) < positionSon=j; //позиция узла по отношению к родителю break; >> //если ptr-первый ребенок (самый левый) if (positionSon==0)< if (parent->children[positionSon+1]->count>(t-1))< //если у правого брата больше, чем t-1 ключей k1=parent->children[positionSon+1]->keys[0]; //k1 - минимальный ключ правого брата k2=parent->keys[positionSon]; //k2 - ключ родителя, больше, чем удаляемый, и меньше, чем k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon]=k1; //меняем местами k1 и k2 removeFromNode(k1, parent->children[positionSon+1]); //удаляем k1 из правого брата > else < //если у правого единственного брата не больше t-1 ключей removeFromNode(key, ptr); if (ptr->count <=(t-2)) repair(ptr); >> else < //если ptr-последний ребенок (самый правый) if (positionSon==parent->count)< //если у левого брата больше, чем t-1 ключей if (parent->children[positionSon-1]->count>(t-1))< BNode *temp=parent->children[positionSon-1]; k1=temp->keys[temp->count-1]; //k1 - максимальный ключ левого брата k2=parent->keys[positionSon-1]; //k2 - ключ родителя, меньше, чем удаляемый и больше, чем k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon-1]=k1; removeFromNode(k1, temp); > else < //если у единственного левого брата не больше t-1 ключей removeFromNode(key, ptr); if (ptr->count <=(t-2)) repair(ptr); >> else < //если ptr имеет братьев справа и слева //если у правого брата больше, чем t-1 ключей if (parent->children[positionSon+1]->count>(t-1))< k1=parent->children[positionSon+1]->keys[0]; //k1 - минимальный ключ правого брата k2=parent->keys[positionSon]; //k2 - ключ родителя, больше, чем удаляемый и меньше, чем k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon]=k1; //меняем местами k1 и k2 removeFromNode(k1, parent->children[positionSon+1]); //удаляем k1 из правого брата > else < //если у левого брата больше, чем t-1 ключей if (parent->children[positionSon-1]->count>(t-1))< BNode *temp=parent->children[positionSon-1]; k1=temp->keys[temp->count-1]; //k1 - максимальный ключ левого брата k2=parent->keys[positionSon-1]; //k2 - ключ родителя, меньше, чем удаляемый и больше, чем k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon-1]=k1; removeFromNode(k1, temp); > else < //если у обоих братьев не больше t-1 ключей removeFromNode(key, ptr); if (ptr->count <=(t-2)) repair(ptr); >> > > >Шестой метод – метод удаления из произвольного узла:
void Tree::remove(int key, BNode *node)< BNode *ptr=node; int position; //номер ключа int i; for (int i=0; icount-1; i++)< if (key==node->keys[i]) < position=i; break; >> int positionSon; //номер сына по отношению к родителю if (ptr->parent!=nullptr)< for(int i=0; iparent->count; i++)< if (ptr->children[i]==ptr) < positionSon==i; break; >> > //находим наименьший ключ правого поддерева ptr=ptr->children[position+1]; int newkey=ptr->keys[0]; while (ptr->leaf==false) ptr=ptr->children[0]; //если ключей в найденном листе не больше 1 - ищем наибольший ключ в левом поддереве //иначе - просто заменяем key на новый ключ, удаляем новый ключ из листа if (ptr->count>(t-1)) < newkey=ptr->keys[0]; removeFromNode(newkey, ptr); node->keys[position]=newkey; > else < ptr=node; //ищем наибольший ключ в левом поддереве ptr=ptr->children[position]; newkey=ptr->keys[ptr->count-1]; while (ptr->leaf==false) ptr=ptr->children[ptr->count]; newkey=ptr->keys[ptr->count-1]; node->keys[position]=newkey; if (ptr->count>(t-1)) removeFromNode(newkey, ptr); else < //если ключей не больше, чем t-1 - перестраиваем removeLeaf(newkey, ptr); >> >И седьмой метод – сам метод удаления, принимающий в качестве входных данных — значение ключа для удаления из дерева.
void Tree::remove(int key)< BNode *ptr=this->root; int position; int positionSon; int i; if (searchKey(key, ptr)==false) < return; >else < //ищем узел, в котором находится ключ для удаления for (i=0; icount-1; i++)< if (ptr->keys[i]!=0) < if(key==ptr->keys[i]) < position=i; break; >else < if ((keykeys[i]))< ptr=ptr->children[i]; positionSon=i; i=-1; > else < if (i==(ptr->count-1)) < ptr=ptr->children[i+1]; positionSon=i+1; i=-1; > > > > else break; > > if (ptr->leaf==true) < if (ptr->count>(t-1)) removeFromNode(key,ptr); else removeLeaf(key, ptr); > else remove(key, ptr); >Вот, как-то так. Надеюсь, кому-то статья будет полезной. Спасибо за внимание.
Источник