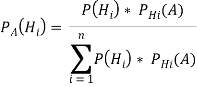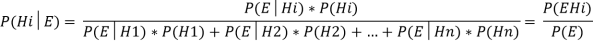Применение байесовского подхода в измерениях аналитических данных как фактор формирования процессов системного экономического развития
Звягин, Л. С. Применение байесовского подхода в измерениях аналитических данных как фактор формирования процессов системного экономического развития / Л. С. Звягин. — Текст : непосредственный // Молодой ученый. — 2017. — № 22 (156). — С. 256-261. — URL: https://moluch.ru/archive/156/44114/ (дата обращения: 15.08.2023).
Байесовская методология отличается от других подходов тем, что еще до получения данных исследователь определяет уровень своего доверия к возможным моделям и впоследствии представляет ее в виде определенных вероятностей. После того, как исследователем получены данные, с использованием теоремы Байеса он находит еще одно множество вероятностей, которые являются пересмотренными степенями доверия к возможным моделям с учетом полученной исследователем новой информации.
Ключевые слова: метод, анализ, прогнозирование, оценки, экономика, экономические процессы
The Bayesian methodology differs from other approaches in that, even before receiving the data, the researcher determines the level of his trust in possible models and subsequently presents it in the form of certain probabilities. After the researcher has obtained the data, using the Bayes theorem he finds another set of probabilities, which are revised degrees of confidence in the possible models, taking into account the new information received by the researcher.
Keywords: method, analysis, forecasting, estimation, economics, economic processes
Байесовские методы разработаны вследствие многочисленных попыток ученых определить проблемы статистического анализа поведения различных процессов и найти их решение с помощью применения основы байесовской методологии — теоремы Байеса. Использование данной теоремы имеет ряд предпосылок, основная из которых — наличие определенных соотношений между вероятностями явлений, имеющих различный характер и спецификации любого явления на нужном уровне [1].
Байесовская методология отличается от других подходов тем, что еще до получения данных исследователь определяет уровень своего доверия к возможным моделям и впоследствии представляет ее в виде определенных вероятностей. После того, как исследователем получены данные, с использованием теоремы Байеса он находит еще одно множество вероятностей, которые являются пересмотренными степенями доверия к возможным моделям с учетом полученной исследователем новой информации.
Одним из ключевых преимуществ байесовского подхода является использование любой начальной (априорной) информации относительно параметров модели. Такая информация выражается в виде априорной вероятности или функции плотности вероятности. Затем начальные вероятности «пересматриваются», с помощью выборочных данных, которые находят свое отображение в виде апостериорного распределения оценок параметров или переменных модели.
Необходимо выделить следующие особенности байесовского подхода:
‒ абсолютно все параметры и величины принято считать случайными, а именно точное значение параметров неизвестно исследователю, из чего следует то, что параметры являются случайными с точки зрения незнания исследователя;
‒ методы Байеса используются даже при нулевом объеме выборки. В этом случае значения априорного и апостериорного распределений равны;
‒ для оценки неизвестных переменных используют апостериорные распределения, то есть, найти решение задачи по оцениванию определенной величины, означает определить апостериорное распределение этой величины;
‒ основным инструментом подхода является формула (теорема) Байеса, а также такие правила, как sum -rule (если A1, …, Ak — взаимоисключающие события, то одно из них происходит всегда) и product — rule (любую совместную плотность всегда можно разбить на множители).
Наряду с вышеперечисленными достоинствами байесовской методологии необходимо выделить ее недостатки. Начиная с 1930 гг. байесовская парадигма довольно часто подвергалась резкой критике и практически не находила применения по следующим причинам:
‒ В байесовских методах предполагается, что априорное распределение известно до начала наблюдений и не предлагается конструктивных способов его выбора;
‒ Принятие решения при использовании байесовских методов в нетривиальных случаях требует колоссальных вычислительных затрат, связанных с численным интегрированием в многомерных пространствах;
‒ Фишером была показана оптимальность метода максимального правдоподобия, а следовательно — бессмысленность попыток придумать что-то лучшее.
На сегодняшний момент (начиная с 1990 гг.) ученые наблюдают возрождение методологии Байеса, методы которой оказались полезными для поиска решений многочисленных и достаточно серьезных вопросов и проблем в сфере машинного обучения и статистики.
Теорема Байеса: формула, применение
Формула (теорема) Байеса является одной из фундаментальных теорем теории вероятностей и позволяет установить вероятность определенного события А, если имеет место возникновение другого взаимозависимого с ним статистически события В. Говоря иначе, применение теоремы Байеса дает возможность исследователю наиболее точно пересчитать вероятность, учитывая как информацию, полученную им ранее, так и новые данные более поздних наблюдений. Байесовская теорема может быть получена из фундаментальных аксиом теории вероятностей, а именно из условной вероятности. Формуле Байеса присущи определенные особенности, главная из которых состоит в том, что для использования теоремы на практике необходимо значительное количество вычислений и расчетов, вследствие этого оценки байесовской парадигмы нашли активное применение только в период после революции, произошедшей в сфере сетевых и компьютерных технологий.
Перед формулированием байесовской теоремы вероятности, используемые в ней, подвергались многочисленным вероятностным интерпретациям. В одной из них устанавливался факт того, что вывод формулы зависит напрямую от использования особого подхода к статистическому анализу. При применении байесовской интерпретации вероятности теорема Байеса показывает, как степень личного доверия способна значительно меняться после определенного числа возникших событий. В этом состоят основные выводы Байеса, ставшие фундаментальными для байесовской статистики. Однако теорема нашла свое применение не только в байесовском анализе, но и активно используется в большом количестве иных расчетов.
Теорема Байеса получила свое название в честь её автора Томаса Байеса (1702–1761) — английского математика, первым предложившего применение сформулированной им теоремы для корректировки убеждений, опираясь на свежеполученную информацию [4].
Сущность байесовской парадигмы состоит в том, что при нахождении исследователем новой информации она дает основу для измерения вероятностей, которые обусловлены связанными между собой событиями. Формула Байеса имеет следующий вид [1]:
,
где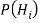 
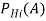
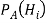
— вероятности гипотез до опыта (априорные вероятности); 
— условные вероятности возникновения события А при выборе i-й гипотезы; 
— условная вероятность i-й гипотезы после возникновения события А (апостериорная или послеопытная вероятность).
С помощью данной теоремы удается изменить значение вероятности на основе более поздних полученных сведений. Интерпретация байесовского подхода имеет следующий вид: пусть к началу реорганизации определенного объекта имеются n гипотез H1, H2, …, Hn о возможных его состояниях. На основе статистических данных за прошлые годы можно приписать им априорные вероятности P(H1), P(H2), …, P(Hn). Затем проводится эксперимент (реализуется проект), в результате которого может наступить или не наступить событие А. Опытным путем определяются условные вероятности возникновения события А при выборе i-й гипотезы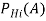 
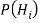
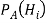
как частоты наблюдения события А. При условии наступления события А делается переоценка веры в справедливость каждой гипотезы посредством замены вероятностей на вероятности .
Необходимо отметить, что в случае отсутствия статистических данных об априорных вероятностях наблюдений или гипотез о возникновении события А байесовскую методологию применить невозможно, так как подобная «формализация» теряет физический смысл [6].
Байесовская стратегия оценки достоверности выводов в экспертных системах
Байесовская стратегия оценки выводов находит все более частое применение в науке, экономике и промышленности. Для детального изучения байесовской стратегии необходимо рассмотреть пример оценки достоверности гипотезы на ее основе, а также обосновать использование теоремы Байеса для экспертных систем.
Для начала необходимо привести более расширенный вариант формулы Байеса с учетом некоторого события Е, связанного с событиями H1, H2. Hn. Вероятности события E известны при том условии, что какое-то из событий H1, H2. Hn наступило: P(E/H1), P(E/H2). P(E/Hn). Предположим, нам известно, что событие E произошло. В этом случае вероятность того, что какое-либо из событий Hi (i=1. n) наступило, определяется по следующей формуле [2]:
События H1, H2. Hn — гипотезы, а событие E называется свидетельством. Вероятности гипотез P(Hi) без учета свидетельства (т. е. без учета того, произошло событие E или нет) называются доопытными (априорными), а вероятности P(Hi/E) — послеопытными (апостериорными). Величина P(EHi) — совместная вероятность событий E и Hi, т. е. вероятность того, что произойдут оба события вместе. Величина P(E) — полная (безусловная) вероятность события E.
В экспертных системах (компьютерные системы, которые способны частично заменить специалиста-эксперта в разрешении конкретной проблемной ситуации) теорема Байеса может использоваться для оценки вероятностей заключений продукционных правил на основе данных о достоверности их посылок. Заключения (выводы) в этом случае соответствуют гипотезам в теореме Байеса, а посылки — свидетельствам. Обычно посылка правила в экспертных системах содержит несколько условий. Вероятности P(Hi) и P(E/Hi) определяются на основе статистических данных с использованием основных формул, применяющихся в теории вероятностей (формулы умножения вероятностей, формулы сложения вероятностей).
В качестве наглядного примера рассмотрим экспертную систему, которая помогает оценить условия труда рабочих в определенной организации. В следующей таблице представлены данные о 5 тыс. рабочих (у 315 обнаружено заболевание, возникшее в связи с их профессиональной деятельностью):
Пример оценки достоверности гипотезы
Кол-во ситуаций обнаружения проф. заболеваний
Кол-во рабочих, укоторых нет проф. заболевания
Контакт с вредными веществами
Источник