Определить количество уровней двоичного дерева поиска
Напишите элемент-функцию depth, принимающую в качестве аргумента двоичное дерево и определяющую, сколько уровней оно содержит.
Вот такое вот, казалось бы, простое задание, которое, тем не менее, привело меня в тупик. Не могу сообразить, как написать эту функцию, может кто-нибудь даст дельный совет, сам, похоже, не смогу решить.
Частотный словарь из слов текстового файла в виде дерева двоичного поиска
Задача: Построить частотный словарь из слов текстового файла в виде дерева двоичного поиска.
Сформировать бинарное дерево поиска и определить максимальную глубину дерева
Добрый день всем. По задаче необходимо сформировать бинарное дерево поиска и определить.
Расчет количества уровней в бинарном дерева
Доброго всем времени суток, есть бинарное дерево с функциями добавления, удаления и печати, нужно.
Пример двоичного дерева
Здравствуйте! Возникла мысль попробовать реализовать двоичное дерево в c++ для этого решил сначала.
int height(Node *node) { if (!node) return 0; int h_l = height(node->left); int h_r = height(node->right); return std::max(h_l, h_r) + 1; }
Сообщение от stzer
Сообщение от stzer
Добавлено через 3 минуты
А если в элемент-функции возвращаемое значение void?
Я суть решения задачи понять не могу, мне код, по большому счёту, не нужен.
Liss29, хорошо. Тут просто используется рекурсия. Допустим, у нас есть дерево T с корнем R. Есть два узла, левый (L) и правый (R). Что имеем: высота дерева T на 1 больше максимальной высоты поддеревьев — max(height(L), height(R)) . Сначала считаем высоту левого поддерева L, потом правого R. Высоту L и R находим аналогично — 1 + max(высота левого поддерева L, высота правого поддерева R). И т.д. Чувствуете рекурсию? Как только опускаемся до узла, у которого нет потомка, рекурсия останавливается.
Все ответы на вопросы можете найти в книге R. Sedgewick. Alghorithms in C++.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
templatetypename T> void ListTreeT>::depthHelper(TreeNodeT>* ptr) { static int left = 0, right = 0; //static int depthPtr; if(ptr != NULL) { depthHelper(ptr->leftPtr); depthHelper(ptr->rightPtr); (ptr->rightPtr != NULL ? right++ : right); (ptr->leftPtr != NULL ? left++ : left); } depthRef = (left > right) ? left : right; }
Вроде бы работает, но нет 100% уверенности.
Добавлено через 3 минуты
Сообщение от stzer
Дейтелов читаю, как только закончу, если желание не отпадёт к изучению языка, то обязательно вернусь к вышеобозначенной книге!
Функция некорректно работает, если у нас дерево, например, такого вида:
Узлы, в которых нет цифр — просто NULL. Ищите ошибку =)
stzer
Как не пробую, ничего не получается. Обходим левое поддерево, затем правое поддерево, а как узнать, что левое поддерево обошли, не могу никак въехать в это(
Добавлено через 3 часа 29 минут
А такой варик:
templatetypename T> void ListTreeT>::depthHelper(TreeNodeT>* ptr) { if(ptr != NULL) { depthRef++; (ptr->leftPtr != NULL) ? depthHelper(ptr->leftPtr) : depthHelper(ptr->rightPtr); } }
Liss29, неа, неправильно. Допустим у узла R есть два не NULL потомка. Функция пойдет рекурсивно исполняться только по левому поддереву, минуя правое. У правого поддерева высота может быть больше.
Сообщение от stzer
Выше я спросил, как задать условие, которое способно определить конец левого поддерева и, если оно существует, начало правого поддерева, всю голову сломал, решения не нашёл
Сообщение от Liss29
Сообщение от zer0mail
ах, ну да, а я тут мозг ..бу себе и другим, так что ли..
Добавлено через 17 часов 6 минут
templatetypename T> void ListTreeT>::depthHelper(TreeNodeT>* ptr) { static int left = 0, right = 0; left = high_left(ptr->leftPtr); right = high_right(ptr->rightPtr); depthRef = (left > right) ? (left + 1) : (right + 1); }
Интересно, а как удалить корневой узел двоичного дерева поиска? Получается, что родительский узел удаляемого элемента будет иметь адрес нуль, если удаляется корневой узел, я пробовал так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
//если родительский узел удаляемого узла нуль if(rootNodeDelete == NULL) //коневой узел удаляемого узла { TreeNodeT>* tempPtr = ptr; //ptr - узел для удаления if(rootNodeR == NULL) //Корневой узел замещающего узла { //rootNodeDelete = new TreeNode(deletePtr->data); //deletePtr - замещающий узел deletePtr->leftPtr = ptr->leftPtr; deletePtr->rightPtr = ptr->rightPtr; } else //если у замещающего узла есть корневое значение { /*deletePtr->leftPtr = ptr->leftPtr; deletePtr->rightPtr = ptr->rightPtr; rootNodeR->leftPtr = NULL;*/ } delete tempPtr; return; }
Хотел указатели корневого значения присвоить замещающему узлу, которое должно стать новым корнем дерева, не знаю, мне это показалось вполне приемлемо. Что я делаю не так?
Но после удаления портирся адрес и в общем-то всё.
Источник
Динамические структуры данных: бинарные деревья
Аннотация: В лекции рассматриваются определения, свойства и виды деревьев, элементы, характеристики и способы объявления деревьев в программах, основные операции над элементами деревьев, понятие и виды обходов деревьев, приводятся примеры реализации основных операций над бинарными деревьями в виде рекурсивных функций.
Цель лекции: изучить понятие, формирование, особенности доступа к данным и работы с памятью в бинарных деревьях, научиться решать задачи с использованием рекурсивных функций и алгоритмов обхода бинарных деревьев в языке C++.
Дерево является одним из важнейших и интересных частных случаев графа. Древовидная модель оказывается довольно эффективной для представления динамических данных с целью быстрого поиска информации .
Деревья являются одними из наиболее широко распространенных структур данных в информатике и программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.
Дерево – это структура данных , представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов ( рис. 31.1). Каждый элемент дерева называется вершиной (узлом) дерева. Вершины дерева соединены направленными дугами, которые называют ветвями дерева. Начальный узел дерева называют корнем дерева, ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.
Каждое дерево обладает следующими свойствами:
- существует узел, в который не входит ни одной дуги (корень);
- в каждую вершину, кроме корня, входит одна дуга.
Деревья особенно часто используют на практике при изображении различных иерархий. Например, популярны генеалогические деревья.
Все вершины, в которые входят ветви, исходящие из одной общей вершины, называются потомками, а сама вершина – предком. Для каждого предка может быть выделено несколько. Уровень потомка на единицу превосходит уровень его предка. Корень дерева не имеет предка, а листья дерева не имеют потомков.
Высота (глубина) дерева определяется количеством уровней, на которых располагаются его вершины. Высота пустого дерева равна нулю, высота дерева из одного корня – единице. На первом уровне дерева может быть только одна вершина – корень дерева , на втором – потомки корня дерева, на третьем – потомки потомков корня дерева и т.д.
Поддерево – часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.
Степенью вершины в дереве называется количество дуг, которое из нее выходит. Степень дерева равна максимальной степени вершины, входящей в дерево . При этом листьями в дереве являются вершины, имеющие степень нуль. По величине степени дерева различают два типа деревьев:
Упорядоченное дерево – это дерево , у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.
Деревья являются рекурсивными структурами, так как каждое поддерево также является деревом. Таким образом, дерево можно определить как рекурсивную структуру, в которой каждый элемент является:
Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.
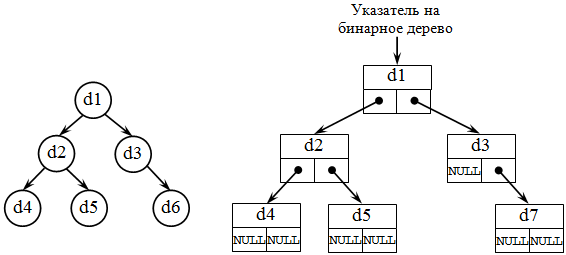
Списочное представление деревьев основано на элементах, соответствующих вершинам дерева. Каждый элемент имеет поле данных и два поля указателей: указатель на начало списка потомков вершины и указатель на следующий элемент в списке потомков текущего уровня. При таком способе представления дерева обязательно следует сохранять указатель на вершину, являющуюся корнем дерева .
Для того, чтобы выполнить определенную операцию над всеми вершинами дерева необходимо все его вершины просмотреть. Такая задача называется обходом дерева.
Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.
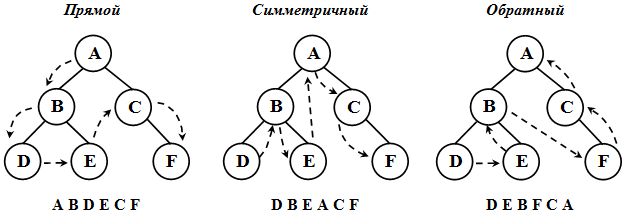
При обходе все вершины дерева должны посещаться в определенном порядке. Существует несколько способов обхода всех вершин дерева. Выделим три наиболее часто используемых способа обхода дерева ( рис. 31.2):
Существует большое многообразие древовидных структур данных. Выделим самые распространенные из них: бинарные (двоичные) деревья, красно-черные деревья, В-деревья, АВЛ-деревья , матричные деревья, смешанные деревья и т.д.
Бинарные деревья
Бинарные деревья являются деревьями со степенью не более двух.
Бинарное (двоичное) дерево – это динамическая структура данных , представляющее собой дерево , в котором каждая вершина имеет не более двух потомков ( рис. 31.3). Таким образом, бинарное дерево состоит из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка .
Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут соответственно:
- информационное поле (ключ вершины);
- служебное поле (их может быть несколько или ни одного);
- указатель на левое поддерево ;
- указатель на правое поддерево .
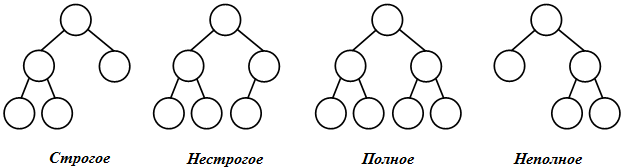
По степени вершин бинарные деревья делятся на ( рис. 31.4):
- строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
- нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).
В общем случае у бинарного дерева на k -м уровне может быть до 2 k-1 вершин. Бинарное дерево называется полным, если оно содержит только полностью заполненные уровни. В противном случае оно является неполным.
Дерево называется сбалансированным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.
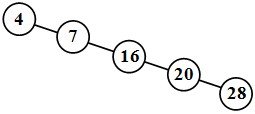
Бинарное дерево может представлять собой пустое множество . Бинарное дерево может выродиться в список ( рис. 31.5).
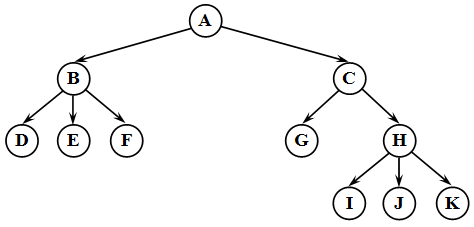
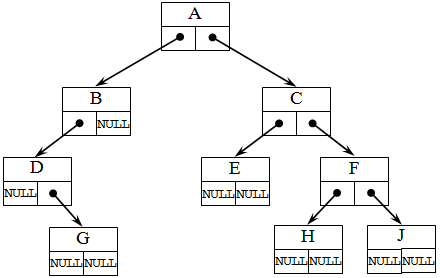
Структура дерева отражается во входном потоке данных так: каждой вводимой пустой связи соответствует условный символ, например, ‘*’ (звездочка). При этом сначала описываются левые потомки, затем, правые. Для структуры бинарного дерева , представленного на следующем рисунке 6, входной поток имеет вид: ABD*G***CE**FH**J** .
Бинарные деревья могут применяться для поиска данных в специально построенных деревьях ( базы данных ), сортировки данных, вычислений арифметических выражений , кодирования (метод Хаффмана) и т.д.
Источник