Alex tools
Бинарное дерево поиска может быть использовано для реализации простого алгоритма сортировки. Как и в случае с heapsort, мы вставляем все значения, которые мы хотим отсортировать, в новую упорядоченную структуру данных — в данном случае это двоичное дерево поиска — и затем перемещаемся по порядку.
Наихудшее время для build_binary_tree — O(n*n) — если вы передаете ему отсортированный список значений, он объединяет их в связанный список без левых поддеревьев. Например, build_binary_tree ([1, 2, 3, 4, 5]) выдает дерево (1 (2 (3 (4 (5)))))).
Есть несколько схем для преодоления этого недостатка с помощью простых бинарных деревьев; наиболее распространенным является самобалансирующееся двоичное дерево поиска. Если эта же процедура выполняется с использованием такого дерева, общее время наихудшего случая составляет O(n log n), что является асимптотически оптимальным для сортировки сравнения. На практике добавленные издержки во времени и пространстве для сортировки на основе дерева (особенно для распределения узлов) делают его уступающим другим асимптотически оптимальным сортировкам, таким как heapsort для сортировки статического списка. С другой стороны, это один из наиболее эффективных методов добавочной сортировки, добавление элементов в список с течением времени при постоянной сортировке списка.
Операции с приоритетной очередью
Деревья двоичного поиска могут служить приоритетными очередями: структурами, которые позволяют вставлять произвольный ключ, а также искать и удалять минимальный (или максимальный) ключ. Вставка работает как объяснено ранее. Find-min идет по дереву, следуя указателям влево, насколько это возможно, не ударяя по листу:
// Условие: T не является листом дерева function find-min(T): while hasLeft(T): T ? left(T) return key(T)
Find-max аналогичен: следуйте правым указателям, насколько это возможно. Delete-min (max) может просто найти минимум (максимум), а затем удалить его. Таким образом, и вставка, и удаление занимают логарифмическое время, так же, как в двоичной куче (binary heap), но в отличие от двоичной кучи и большинства других реализаций очереди с приоритетами, одно дерево может поддерживать все функции find-min, find-max, delete-min и одновременно delete-max, что делает бинарные деревья поиска подходящими в качестве двусторонних очередей с приоритетами.
Источник
Структуры данных: бинарные деревья. Часть 1
Этой статьей я начинаю цикл статей об известных и не очень структурах данных а так же их применении на практике.
В своих статьях я буду приводить примеры кода сразу на двух языках: на Java и на Haskell. Благодаря этому можно будет сравнить императивный и функциональный стили программирования и увидить плюсы и минусы того и другого.
Начать я решил с бинарных деревьев поиска, так как это достаточно базовая, но в то же время интересная штука, у которой к тому же существует большое количество модификаций и вариаций, а так же применений на практике.
Зачем это нужно?
Бинарные деревья поиска обычно применяются для реализации множеств и ассоциативных массивов (например, set и map в с++ или TreeSet и TreeMap в java). Более сложные применения включают в себя ropes (про них я расскажу в одной из следующих статей), различные алгоритмы вычислительной геометрии, в основном в алгоритмах на основе «сканирующей прямой».
В этой статье деревья будут рассмотрены на примере реализации ассоциативного массива. Ассоциативный массив — обобщенный массив, в котором индексы (их обычно называют ключами) могут быть произвольными.
Ну-с, приступим
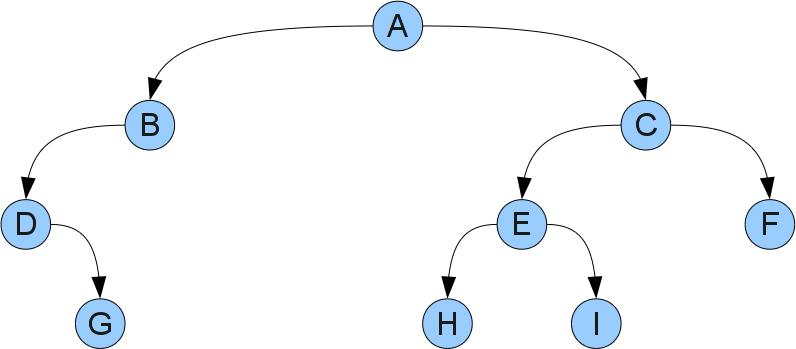
Двоичное дерево состоит из вершин и связей между ними. Конкретнее, у дерева есть выделенная вершина-корень и у каждой вершины может быть левый и правый сыновья. На словах звучит несколько сложно, но если взглянуть на картинку все становится понятным:
У этого дерева корнем будет вершина A. Видно, что у вершины D отсутствует левый сын, у вершины B — правый, а у вершин G, H, F и I — оба. Вершины без сыновей принято называть листьями.
Каждой вершине X можно сопоставить свое дерево, состоящее из вершины, ее сыновей, сыновей ее сыновей, и т.д. Такое дерево называют поддеревом с корнем X. Левым и правым поддеревьями X называют поддеревья с корнями соответственно в левом и правом сыновьях X. Заметим, что такие поддеревья могут оказаться пустыми, если у X нет соответствующего сына.
Данные в дереве хранятся в его вершинах. В программах вершины дерева обычно представляют структурой, хранящей данные и две ссылки на левого и правого сына. Отсутствующие вершины обозначают null или специальным конструктором Leaf:
data Ord key => BSTree key value = Leaf | Branch key value (BSTree key value) (BSTree key value) deriving (Show) static class Node < T1 key; T2 value; Nodeleft, right; Node(T1 key, T2 value) < this.key = key; this.value = value; >> Как видно из примеров, мы требуем от ключей, чтобы их можно было сравнивать между собой ( Ord a в haskell и T1 implements Comparable в java). Все это не спроста — для того, чтобы дерево было полезным данные должны храниться в нем по каким-то правилам.
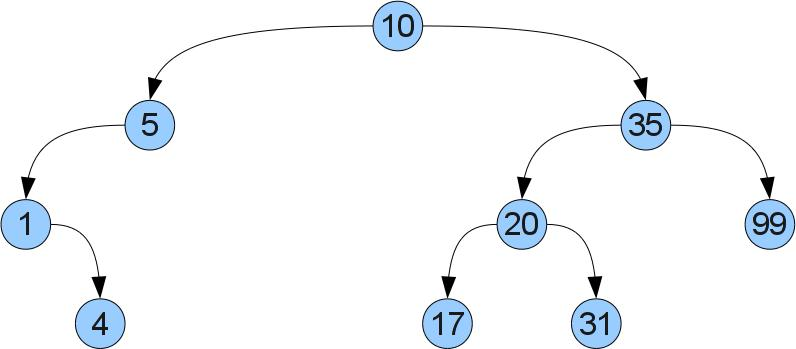
Какие же это правила? Все просто: если в вершине X хранится ключ x, то в левом (правом) поддереве должны храниться только ключи меньшие (соответственно большие) чем x. Проиллюстрируем:
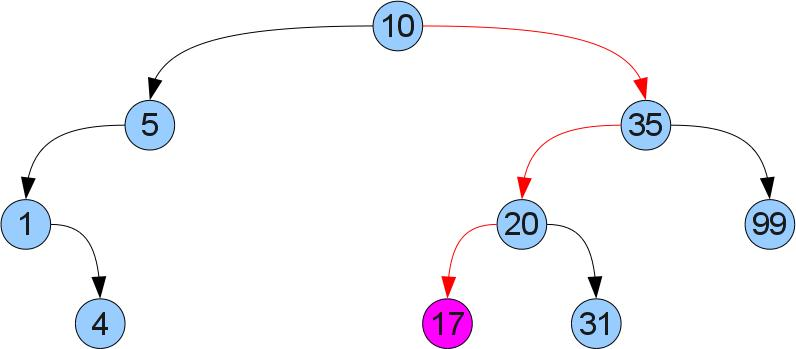
Что же нам дает такое упорядочевание? То, что мы легко можем отыскать требуемый ключ x в дереве! Просто сравним x со значением в корне. Если они равны, то мы нашли требуемое. Если же x меньше (больше), то он может оказаться только в левом (соответственно правом) поддереве. Пусть например мы ищем в дереве число 17:
Функция, получающая значение по ключу:
get :: Ord key => BSTree key value -> key -> Maybe value get Leaf _ = Nothing get (Branch key value left right) k | k < key = get left k | k >key = get right k | k == key = Just value public T2 get(T1 k) < Nodex = root; while (x != null) < int cmp = k.compareTo(x.key); if (cmp == 0) < return x.value; >if (cmp < 0) < x = x.left; >else < x = x.right; >> return null; > Добавление в дерево
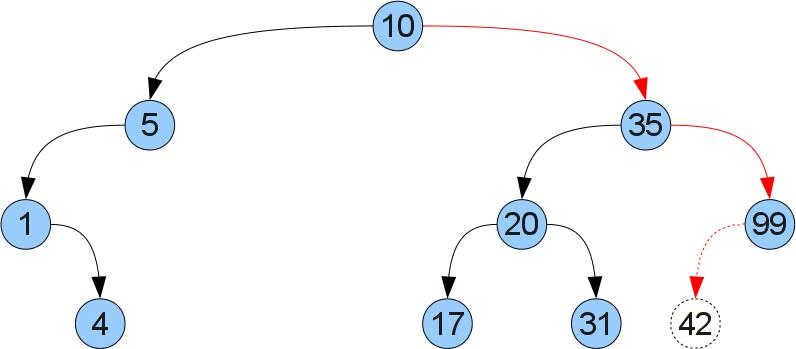
Теперь попробуем сделать операцию добавления новой пары ключ/значение (a,b). Для этого будем спускаться по дереву как в функции get, пока не найдем вершину с таким же ключем, либо не дойдем до отсутсвующего сына. Если мы нашли вершину с таким же ключем, то просто меняем соответствующее значение. В противно случае легко понять что именно в это место следует вставить новую вершину, чтобы не нарушить порядок. Рассмотрим вставку ключа 42 в дерево на прошлом рисунке:
add :: Ord key => BSTree key value -> key -> value -> BSTree key value add Leaf k v = Branch k v Leaf Leaf add (Branch key value left right) k v | k < key = Branch key value (add left k v) right | k >key = Branch key value left (add right k v) | k == key = Branch key value left right public void add(T1 k, T2 v) < Nodex = root, y = null; while (x != null) < int cmp = k.compareTo(x.key); if (cmp == 0) < x.value = v; return; >else < y = x; if (cmp < 0) < x = x.left; >else < x = x.right; >> > Node newNode = new Node(k, v); if (y == null) < root = newNode; >else < if (k.compareTo(y.key) < 0) < y.left = newNode; >else < y.right = newNode; >> > Лирическое отступление о плюсах и минусах функционального подхода
Если внимательно рассмотреть примеры на обоих языках, можно увидеть некоторое различие в поведении функциональной и императивной реализаций: если на java мы просто модифицируем данные и ссылки в имеющихся вершинах, то версия на haskell создает новые вершины вдоль всего пути, пройденного рекурсией. Это связано с тем, что в чисто функциональных языках нельзя делать разрушающие присваивания. Ясно, что это ухудшает производительность и увеличивает потребляемую память. С другой стороны, у такого подхода есть и положительные стороны: отсутствие побочных эффектов сильно облегчает понимание того, как функционирует программа. Более подробно об этом можно прочитать в практически любом учебнике или вводной статье про функциональное программирование.
В этой же статье я хочу обратить внимание на другое следствие функционального подхода: даже после добавления в дерево нового элемента старая версия останется доступной! За счет этого эффекта работают ropes, в том числе и в реализации на императивных языках, позволяя реализовывать строки с асимптотически более быстрыми операциями, чем при традиционном подходе. Про ropes я расскажу в одной из следующих статей.
Вернемся к нашим баранам
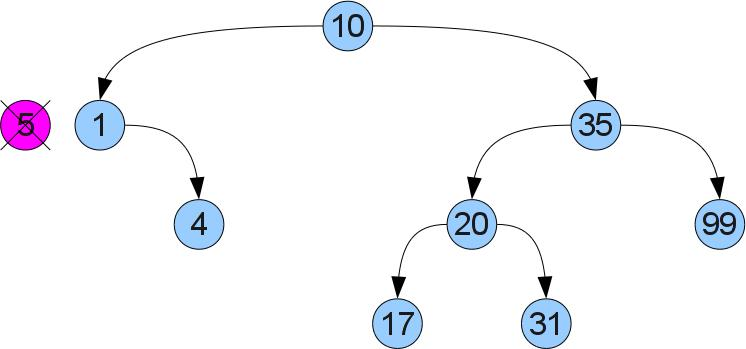
Теперь мы подобрались к самой сложной операции в этой статье — удалению ключа x из дерева. Для начала мы, как и раньше, найдем нашу вершину в дереве. Теперь возникает два случая. Случай 1 (удаляем число 5):
Видно, что у удаляемой вершины нет правого сына. Тогда мы можем убрать ее и вместо нее вставить левое поддерево, не нарушая упорядоченность:
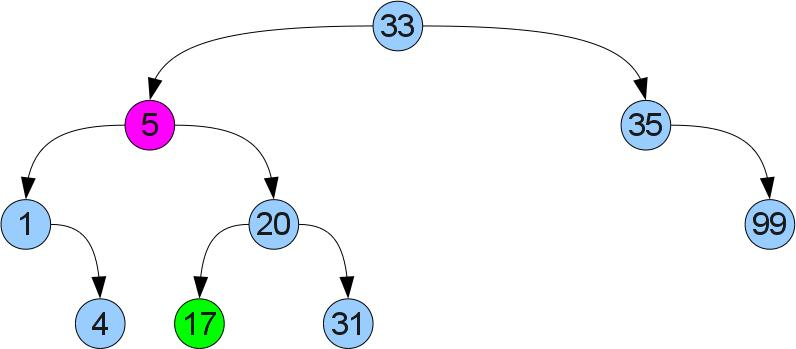
Если же правый сын есть, налицо случай 2 (удаляем снова вершину 5, но из немного другого дерева):
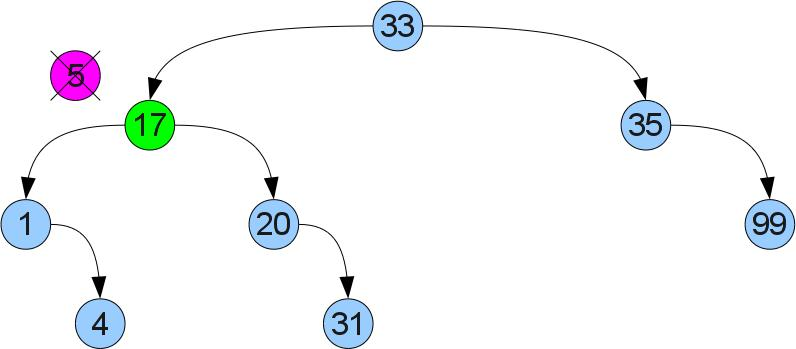
Тут так просто не получится — у левого сына может уже быть правый сын. Поступим по-другому: найдем в правом поддереве минимум. Ясно, что его можно найти если начать в правом сыне и идти до упора влево. Т.к у найденного минимума нет левого сына, можно вырезать его по аналогии со случаем 1 и вставить его вместо удалеемой вершины. Из-за того что он был минимальным в правом поддереве, свойство упорядоченности не нарушится:
remove :: Ord key => BSTree key value -> key -> BSTree key value remove Leaf _ = Leaf remove (Branch key value left right) k | k < key = Branch key value (remove left k) right | k >key = Branch key value left (remove right k) | k == key = if isLeaf right then left else Branch leftmostA leftmostB left right' where isLeaf Leaf = True isLeaf _ = False ((leftmostA, leftmostB), right') = deleteLeftmost right deleteLeftmost (Branch key value Leaf right) = ((key, value), right) deleteLeftmost (Branch key value left right) = (pair, Branch key value left' right) where (pair, left') = deleteLeftmost left public void remove(T1 k) < Nodex = root, y = null; while (x != null) < int cmp = k.compareTo(x.key); if (cmp == 0) < break; >else < y = x; if (cmp < 0) < x = x.left; >else < x = x.right; >> > if (x == null) < return; >if (x.right == null) < if (y == null) < root = x.left; >else < if (x == y.left) < y.left = x.left; >else < y.right = x.left; >> > else < NodeleftMost = x.right; y = null; while (leftMost.left != null) < y = leftMost; leftMost = leftMost.left; >if (y != null) < y.left = leftMost.right; >else < x.right = leftMost.right; >x.key = leftMost.key; x.value = leftMost.value; > > На десерт, пара функций, которые я использовал для тестирования:
fromList :: Ord key => [(key, value)] -> BSTree key value fromList = foldr (\(key, value) tree -> add tree key value) Leaf toList :: Ord key => BSTree key value -> [(key, value)] toList tree = toList' tree [] where toList' Leaf list = list toList' (Branch key value left right) list = toList' left ((key, value):(toList' left list)) Чем же все это полезно?
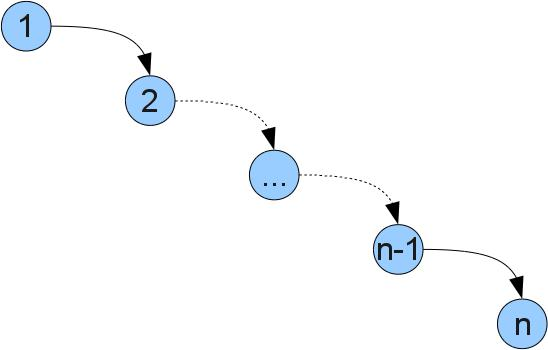
У читателя возможно возникает вопрос, зачем нужны такие сложности, если можно просто хранить список пар [(ключ, значение)]. Ответ прост — операции с деревом работают быстрее. При реализации списком все функции требуют O(n) действий, где n — размер структуры. (Запись O(f(n)) грубо говоря означает «пропорционально f(n)», более корректное описание и подробности можно почитать тут). Операции с деревом же работают за O(h), где h — максимальная глубина дерева (глубина — расстояние от корня до вершины). В оптимальном случае, когда глубина всех листьев одинакова, в дереве будет n=2^h вершин. Значит, сложность операций в деревьях, близких к оптимуму будет O(log(n)). К сожалению, в худшем случае дерево может выродится и сложность операций будет как у списка, например в таком дереве (получится, если вставлять числа 1..n по порядку):
К счастью, существуют способы реализовать дерево так, чтобы оптимальная глубина дерева сохранялась при любой последовательности операций. Такие деревья называют сбалансированными. К ним например относятся красно-черные деревья, AVL-деревья, splay-деревья, и т.д.
Анонс следующих серий
В следующей статье я сделаю небольшой обзор различных сбалансированных деревьев, их плюсы и минусы. В следующих статьях я расскажу о каком-нибудь (возможно нескольких) более подробно и с реализацией. После этого я расскажу о реализации ropes и других возможных расширениях и применениях сбалансированных деревьев.
Полезные ссылки
Исходники примеров целиком:
Также очень советую почитать книгу Кормен Т., Лейзерсон Ч., Ривест Р.: «Алгоритмы: построение и анализ», которая является прекрасным учебником по алгоритмам и структурам данных
Источник