Бинарное дерево сортировка алгоритм

Сортировка с помощью двоичного дерева

Сортировка с помощью двоичного дерева (сортировка двоичным деревом, сортировка деревом, древесная сортировка, сортировка с помощью бинарного дерева, англ. tree sort ) — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например с файла, сокета или консоли).

Алгоритм

1. Построение двоичного дерева.

2. Сборка результирующего массива путём обхода узлов в необходимом порядке следования ключей.

Эффективность

Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log(n)). Соответственно, для n объектов сложность будет составлять O(n log(n)), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n²).

При физическом развёртывании древовидной структуры в памяти требуется не менее чем 4n ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист), однако, существуют способы уменьшить требуемую дополнительную память.

Примеры реализации

В простой форме функционального программирования на Haskell данный алгоритм будет выглядеть так:

data Tree a = Leaf | Node (Tree a) a (Tree a) insert :: Ord a => a -> Tree a -> Tree a insert x Leaf = Node Leaf x Leaf insert x (Node t y t') | x insert x (Node t y t') | x > y = Node t y (insert x t') flatten :: Tree a -> [a] flatten Leaf = [] flatten (Node t x t') = flatten t ++ [x] ++ flatten t' treesort :: Ord a => [a] -> [a] treesort = flatten . foldr insert Leaf

#include #include #include template typename Iterator> void binary_tree_sort(Iterator begin, Iterator end)  std::multisettypename std::iterator_traitsIterator>::value_type> tree(begin, end); std::copy(tree.begin(), tree.end(), begin); >; 

Пример создания бинарного дерева и сортировки на языке Java:

// Скомпилируйте и введите java TreeSort class Tree  public Tree left; // левое и правое поддеревья и ключ public Tree right; public int key; public Tree(int k)  // конструктор с инициализацией ключа key = k; > /* insert (добавление нового поддерева (ключа)) сравнить ключ добавляемого поддерева (К) с ключом корневого узла (X). Если K>=X, рекурсивно добавить новое дерево в правое поддерево. Если K public void insert( Tree aTree)  if ( aTree.key  key ) if ( left != null ) left.insert( aTree ); else left = aTree; else if ( right != null ) right.insert( aTree ); else right = aTree; > /* traverse (обход) Рекурсивно обойти левое поддерево. Применить функцию f (печать) к корневому узлу. Рекурсивно обойти правое поддерево. */ public void traverse(TreeVisitor visitor)  if ( left != null) left.traverse( visitor ); visitor.visit(this); if ( right != null ) right.traverse( visitor ); > > interface TreeVisitor  public void visit(Tree node); >; class KeyPrinter implements TreeVisitor  public void visit(Tree node)  System.out.println( " " + node.key ); > >; public class TreeSort  public static void main(String args[])  Tree myTree; myTree = new Tree( 7 ); // создать дерево (с ключом) myTree.insert( new Tree( 5 ) ); // присоединять поддеревья myTree.insert( new Tree( 9 ) ); myTree.traverse(new KeyPrinter()); > > 

См. также

Источник

Сортировка бинарным деревом

Сортировка бинарным деревом (Tree sort) – алгоритм сортировки, который заключается в построении двоичного дерева поиска по ключам массива, с последующим построением результирующего массива упорядоченных элементов путем обхода дерева.

Принцип работы алгоритма сортировки бинарным деревом

• Элементы неотсортированного массива данных добавляются в двоичное дерево поиска;
• Для получения отсортированного массива, производится обход бинарного дерева с переносом данных из дерева в результирующий массив.

Реализация алгоритма сортировки бинарным деревом

using System; using System.Collections.Generic; namespace TreeSortApp < //простая реализация бинарного дерева public class TreeNode < public TreeNode(int data) < Data = data; >//данные public int Data < get; set; > //левая ветка дерева public TreeNode Left < get; set; > //правая ветка дерева public TreeNode Right < get; set; > //рекурсивное добавление узла в дерево public void Insert(TreeNode node) < if (node.Data < Data) < if (Left == null) < Left = node; >else < Left.Insert(node); >> else < if (Right == null) < Right = node; >else < Right.Insert(node); >> > //преобразование дерева в отсортированный массив public int[] Transform(Listint> elements = null) < if (elements == null) < elements = new Listint>(); > if (Left != null) < Left.Transform(elements); >elements.Add(Data); if (Right != null) < Right.Transform(elements); >return elements.ToArray(); > > class Program < //метод для сортировки с помощью двоичного дерева private static int[] TreeSort(int[] array) < var treeNode = new TreeNode(array[0]); for (int i = 1; i < array.Length; i++) < treeNode.Insert(new TreeNode(array[i])); > return treeNode.Transform(); > static void Main(string[] args) < Console.Write("n hljs-keyword">var n = int.Parse(Console.ReadLine()); var a = new int[n]; var random = new Random(); for (int i = 0; i < a.Length; i++) < a[i] = random.Next(0, 100); > Console.WriteLine("Random Array: ", string.Join(" ", a)); Console.WriteLine("Sorted Array: ", string.Join(" ", TreeSort(a))); > > > 

Источник

Сортировка с помощью дерева

Сортировка с помощью дерева осуществляется на основе бинарного дерева поиска.

Бинарное (двоичное) дерево поиска – это бинарное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):

• оба поддерева – левое и правое, являются двоичными деревьями поиска;
• у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, чем значение ключа данных самого узла X;
• у всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, чем значение ключа данных узла X.

Данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.

Для сортировки с помощью дерева исходная сортируемая последовательность представляется в виде структуры данных «дерево».

Например, исходная последовательность имеет вид:

4, 3, 5, 1, 7, 8, 6, 2

Корнем дерева будет начальный элемент последовательности. Далее все элементы, меньшие корневого, располагаются в левом поддереве, все элементы, большие корневого, располагаются в правом поддереве. Причем это правило должно соблюдаться на каждом уровне.

После того, как все элементы размещены в структуре «дерево», необходимо вывести их, используя инфиксную форму обхода.

Реализация сортировки с помощью дерева на C++

#include
using namespace std;
// Структура — узел дерева
struct tnode
int field; // поле данных
struct tnode *left; // левый потомок
struct tnode *right; // правый потомок
>;
// Вывод узлов дерева (обход в инфиксной форме)
void treeprint(tnode *tree)
if (tree != NULL ) < //Пока не встретится пустой узел
treeprint(tree->left); //Рекурсивная функция вывода левого поддерева
cout field treeprint(tree->right); //Рекурсивная функция вывода правого поддерева
>
>
// Добавление узлов в дерево
struct tnode * addnode( int x, tnode *tree) if (tree == NULL ) // Если дерева нет, то формируем корень
tree = new tnode; //память под узел
tree->field = x; //поле данных
tree->left = NULL ;
tree->right = NULL ; //ветви инициализируем пустотой
>
else // иначе
if (x < tree->field) //Если элемент x меньше корневого, уходим влево
tree->left = addnode(x, tree->left); //Рекурсивно добавляем элемент
else //иначе уходим вправо
tree->right = addnode(x, tree->right); //Рекурсивно добавляем элемент
return (tree);
>
//Освобождение памяти дерева
void freemem(tnode *tree)
if (tree != NULL ) // если дерево не пустое
freemem(tree->left); // рекурсивно удаляем левую ветку
freemem(tree->right); // рекурсивно удаляем правую ветку
delete tree; // удаляем корень
>
>
// Тестирование работы
int main()
struct tnode *root = 0; // Объявляем структуру дерева
system( «chcp 1251» ); // переходим на русский язык в консоли
system( «cls» );
int a; // текущее значение узла
// В цикле вводим 8 узлов дерева
for ( int i = 0; i < 8; i++)
cout cin >> a;
root = addnode(a, root); // размещаем введенный узел на дереве
>
treeprint(root); // выводим элементы дерева, получаем отсортированный массив
freemem(root); // удаляем выделенную память
cin.get(); cin.get();
return 0;
>

Результат выполнения

Комментариев к записи: 3

Источник

2 Алгоритм бинарного дерева

Сортировка с помощью бинарного дерева — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например, с файла, сокета или консоли) [6].

Реализация алгоритма бинарного дерева на языке С#:

public TreeItem LeftChild;

public TreeItem RightChild;

TreeItem top; int n = 0;

private void Add(int a)

TreeItem temp = new TreeItem();

private void Build(TreeItem t)

public void Sort(int[] mas)

>

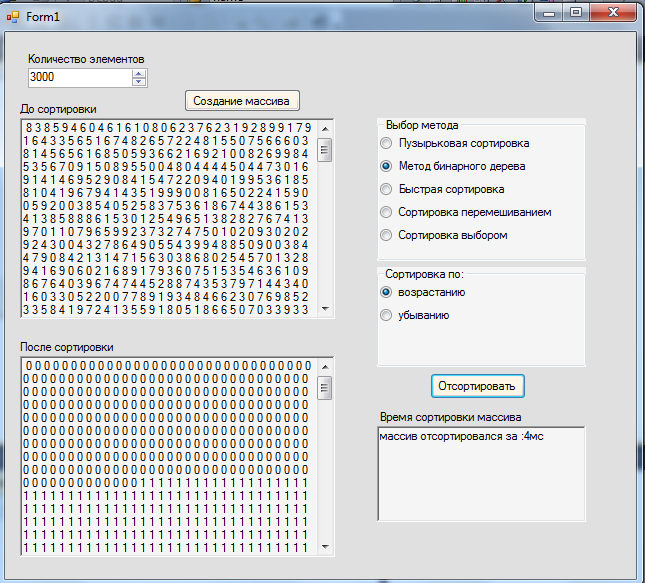
Рисунок 3 – Реализация программы, которая сортирует по возрастанию массив из 3000 элементов методом бинарного дерева за 4 миллисекунды.

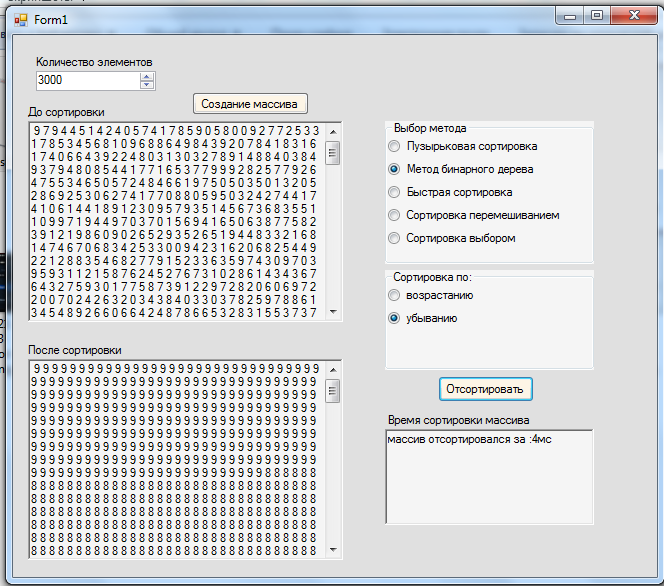
Рисунок 4 – Реализация программы, которая сортирует по убыванию массив из 3000 элементов методом бинарного дерева за 4 миллисекунды.

3 Быстрая сортировка

Основная стратегия ускорения алгоритмов сортировка — обмены между как можно более дальними элементами исходного файла — в методе быстрой сортировки реализована за счет того, что один из ключей в исходном файле используется для разделения его на два подфайла так, чтобы слева от выбранного элемента находились только элементы с меньшими ключами, а справа — только с большими. Элемент, разделяющий файл, помещается между его двумя подфайлами и процедура выполняется рекурсивно для каждой половины до тех пор, пока в очередном новом подфайле не окажется меньше, чем М элементов, где М — заранее выбранное число.

Сортировка подфайлов, содержащих меньше чем М элементов, выполняется каким-либо простым методом, например, простыми вставками. Таким образом, реализация метода зависит от двух параметров: значения М и способа выбора элемента, который предназначен для разделения файла на две части.

Блок выбора Х в простейшем случае формулируется как X=K[l], однако это может привести к крайне неэффективному алгоритму. Наиболее простое лучшее решение — выбирать Х как случайный ключ из диапазона K[l] . K[r] и обменять его с K[l] [4].

Реализация алгоритма быстрой сортировки на языке С#:

public void sorting(int[] mas, long first, long last)

int p = mas[(last — first) / 2 + first];

long i = first, j = last;

Источник