Поиск информации в бд с использованием структуры типа «бинарное дерево».
В задачах поиска предполагается, что все данные хранятся в памяти с определенной идентификацией и, говоря о доступе, имеют в виду, доступ к ключам, однозначно идентифицирующим связанные с ними совокупности данных. Существуют 2 класса методов, реализующих доступ к данным по ключу: методы поиска по дереву и методы хеширования.
Деревом называется конечное множество, состоящее из одного или более элементов, называемых узлами, таких, что:
- Между узлами имеет место отношение типа «исходный-порожденный»;
- Есть только один узел, не имеющий исходного. Он называется корнем;
- Все узлы за исключением корня имеют только один исходный; каждый узел может иметь несколько порожденных;
- Отношение «исходный-порожденный» действует только в одном направлении, т.е. ни один потомок некоторого узла не может стать для него предком.
Число порожденных отдельного узла (число поддеревьев данного корня) называется его степенью. Узел с нулевой степенью называют листом или концевым узлом. Максимальное значение степени всех узлов данного дерева называется степенью дерева.
Если в дереве между порожденными узлами, имеющими общий исходный, считается существенным их порядок, то дерево называется упорядоченным. В задачах поиска почти всегда рассматриваются упорядоченные деревья.
Упорядоченное дерево, степень которого не больше 2 называется бинарным деревом. Бинарное дерево особенно часто используется при поиске в оперативной памяти. Алгоритм поиска: вначале аргумент поиска сравнивается с ключом, находящимся в корне. Если аргумент совпадает с ключом, поиск закончен, если же не совпадает, то в случае, когда аргумент оказывается меньше ключа, поиск продолжается в левом поддереве, а в случае когда больше ключа — в правом поддереве. Увеличив уровень на 1 повторяют сравнение, считая текущий узел корнем.
Дан список студентов, содержащий их фамилии и средний бал успеваемости. В качестве ключа используется фамилия. Предположим, что все записи имеют фиксированную длину, тогда в качестве указателя можно использовать номер записи. Смещение записи в файле в этом случае будет вычислятся как ([номер_записи] -1) * [длина_записи].
Пусть аргумент поиска = «Петров». На рисунке показан один из возможных для этого набора данных бинарных деревьев поиска и путь поиска.
Поиск по бинарному дереву:
Здесь используется следующее правило сравнения строк: значение символа соответствует его порядковому номеру в алфавите. Поэтому «И» меньше «К», а «К» меньше «С». Если текущие символы в сравниваемых строках совпадают, то сравниваются символы в следующих позициях.
Бинарные деревья особенно эффективны в случае когда множество ключей заранее неизвестно, либо когда это множество интенсивно изменяется.
Поиск информации в бд с использованием структуры типа «сильно ветвящееся дерево».
При поиске данных во внешней памяти очень важной является проблема сокращения числа перемещений данных из внешней памяти в оперативную. Поэтому, в данном случае по сравнению с бинарными деревьями более выгодными окажутся сильно ветвящиеся деревья — т.к. их высота меньше, то при поиске потребуется меньше обращений к внешней памяти. Наибольшее применение в этом случае получили В-деревья (В — balanced)
Определение: В-деревом порядка n называется сильно ветвящееся дерево степени 2n+1, обладающее следующими свойствами:
- Каждый узел, за исключением корня, содержит не менее n и не более 2n ключей.
- Корень содержит не менее одного и не более 2n ключей.
- Все листья расположены на одном уровне.
- Каждый нелистовой узел содержит два списка: упорядоченный по возрастанию значений список ключей и соответсвующий ему список указателей (для листовых узлов список указателей отсутствует).
- сравнительно просто может быть организован последовательный доступ, т.к. все листья расположены на одном уровне;
- при добавлении и изменении ключей все изменения ограничиваются, как правило, одним узлом.
В-дерево, в котором истинные значения содержатся только в листьях (концевых узлах), называется В+-деревом. Во внутренних узлах такого дерева содержатся ключи-разделители, задающие диапазон изменения ключей для поддеревьев. Следует отметить, что B-деревья наилучшим образом подходят только для организации доступа к достаточно простым (одномерным) структурам данных.
Источник
Структура данных B-дерево
Всем привет! Мы запустили новый набор на курс «Алгоритмы для разработчиков» и сегодня хотим поделиться интересным переводом, подготовленным для студентов данного курса.
В деревьях поиска, таких как двоичное дерево поиска, AVL дерево, красно-чёрное дерево и т.п. каждый узел содержит только одно значение (ключ) и максимум двое потомков. Однако есть особый тип дерева поиска, который называется B-дерево (произносится как Би-дерево). В нем узел содержит более одного значения (ключа) и более двух потомков. B-дерево было разработано в 1972 году Байером и МакКрейтом и называлось Сбалансированное по высоте дерево поиска порядка m (Height Balanced m-way Search Tree). Свое современное название B-дерево получило позже.
B-дерево можно определить следующим образом:
B-дерево – это сбалансированное дерево поиска, в котором каждый узел содержит множество ключей и имеет более двух потомков.
Здесь количество ключей в узле и количество его потомков зависит от порядка B-дерева. Каждое B-дерево имеет порядок.
B-дерево порядка m обладает следующими свойствами:
Свойство 1: Глубина всех листьев одинакова.
Свойство 2: Все узлы, кроме корня должны иметь как минимум (m/2) – 1 ключей и максимум m-1 ключей.
Свойство 3: Все узлы без листьев, кроме корня (т.е. все внутренние узлы), должны иметь минимум m/2 потомков.
Свойство 4: Если корень – это узел не содержащий листьев, он должен иметь минимум 2 потомка.
Свойство 5:Узел без листьев с n-1 ключами должен иметь n потомков.
Свойство 6: Все ключи в узле должны располагаться в порядке возрастания их значений.
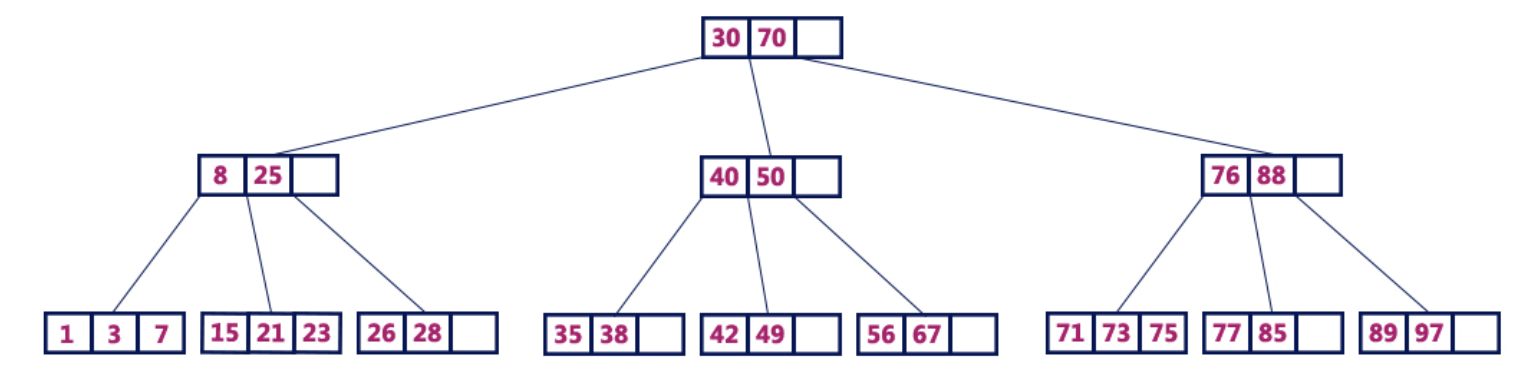
Например, B-дерево 4 порядка содержит максимум 3 значения ключа и максимум 4 потомка для каждого узла.
B-дерево 4 порядка
Операции над B-деревом
Поиск по B-дереву аналогичен поиску по двоичному дереву поиска. В двоичном дереве поиска поиск начинается с корня и каждый раз принимается двустороннее решение (пойти по левому поддереву или по правому). В В-дереве поиск также начинается с корневого узла, но на каждом шаге принимается n-стороннее решение, где n – это общее количество потомков рассматриваемого узла. В В-дереве сложность поиска составляет O(log n). Поиск происходит следующим образом:
Шаг 1: Считать элемент для поиска.
Шаг 2: Сравнить искомый элемент с первым значением ключа в корневом узле дерева.
Шаг 3: Если они совпадают, вывести: «Искомый узел найден!» и завершить поиск.
Шаг 4: Если они не совпадают, проверить больше или меньше значение элемента, чем текущее значение ключа.
Шаг 5: Если искомый элемент меньше, продолжить поиск по левому поддереву.
Шаг 6: Если искомый элемент больше, сравнить элемент со следующим значением ключа в узле и повторять Шаги 3, 4, 5 и 6 пока не будет найдено совпадение или пока искомый элемент не будет сравнен с последним значением ключа в узле-листе.
Шаг 7: Если последнее значение ключа в узле-листе не совпало с искомым, вывести «Элемент не найден!» и завершить поиск.
Операция вставки в B-дерево
В В-дереве новый элемент может быть добавлен только в узел-лист. Это значит, что новая пара ключ-значение всегда добавляется только к узлу-листу. Вставка происходит следующим образом:
Шаг 1: Проверить пустое ли дерево.
Шаг 2: Если дерево пустое, создать новый узел с новым значением ключа и его принять за корневой узел.
Шаг 3: Если дерево не пустое, найти подходящий узел-лист, к которому будет добавлено новое значение, используя логику дерева двоичного поиска.
Шаг 4: Если в текущем узле-листе есть незанятая ячейка, добавить новый ключ-значение к текущему узлу-листу, следуя возрастающему порядку значений ключей внутри узла.
Шаг 5: Если текущий узел полон и не имеет свободных ячеек, разделите узел-лист, отправив среднее значение родительскому узлу. Повторяйте шаг, пока отправляемое значение не будет зафиксировано в узле.
Шаг 6: Если разделение происходит с корнем дерева, тогда среднее значение становится новым корнем дерева и высота дерева увеличивается на единицу.
Давайте создадим B-дерево порядка 3, добавляя в него числа от 1 до 10.
Insert(1):
Поскольку «1» — это первый элемент дерева – он вставляется в новый узел и этот узел становится корнем дерева.
Insert(2):
Элемент «2» добавляется к существующему узлу-листу. Сейчас у нас всего один узел, следовательно он является и корнем и листом одновременно. В этом листе имеется пустая ячейка. Тогда «2» встает в эту пустую ячейку.
Insert(3):
Элемент «3» добавляется к существующему узлу-листу. Сейчас у нас только один узел, который одновременно является и корнем и листом. У этого листа нет пустой ячейки. Поэтому мы разделяем этот узел, отправляя среднее значение (2) в родительский узел. Однако у текущего узла родительского узла нет. Поэтому среднее значение становится корневым узлом дерева.
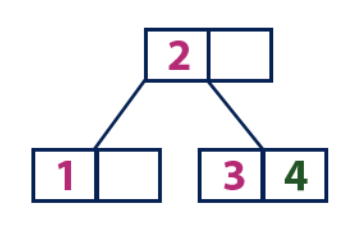
Insert(4):
Элемент «4» больше корневого узла со значением «2», при этом корневой узел не является листом. Поэтому мы двигаемся по правому поддереву от «2». Мы приходим к узлу-листу со значением «3», у которого имеется пустая ячейка. Таким образом, мы можем вставить элемент «4» в эту пустую ячейку.
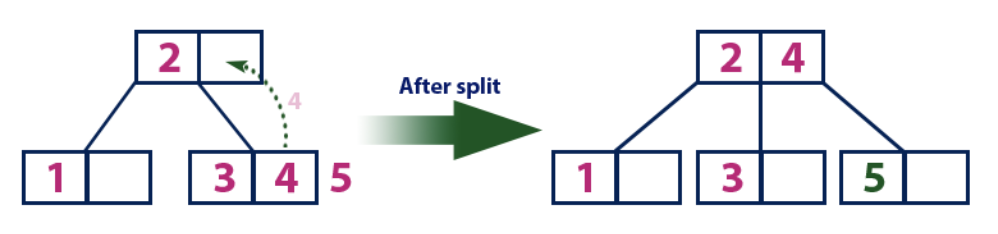
Insert(5):
Элемент «5» больше корневого узла со значением «2», при этом корневой узел не является листом. Поэтому мы двигаемся по правому поддереву от «2». Мы приходим к узлу-листу и обнаруживаем, что он уже полон и не имеет пустых ячеек. Тогда мы делим этот узел, отправляя среднее значение (4) в родительский узел (2). В родительском узле есть для него пустая ячейка, поэтому значение «4» добавляется к узлу, в котором уже есть значение «2», а новый элемент «5» добавляется в качестве нового листа.
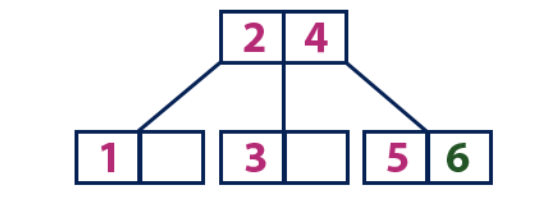
Insert(6):
Элемент «6» больше, чем элементы корня «2» и «4», который не является листом. Мы двигаемся по правому поддереву от элемента «4». Мы достигаем листа со значением «5», у которого есть пустая ячейка, поэтому элемент «6» помещаем как раз в нее.
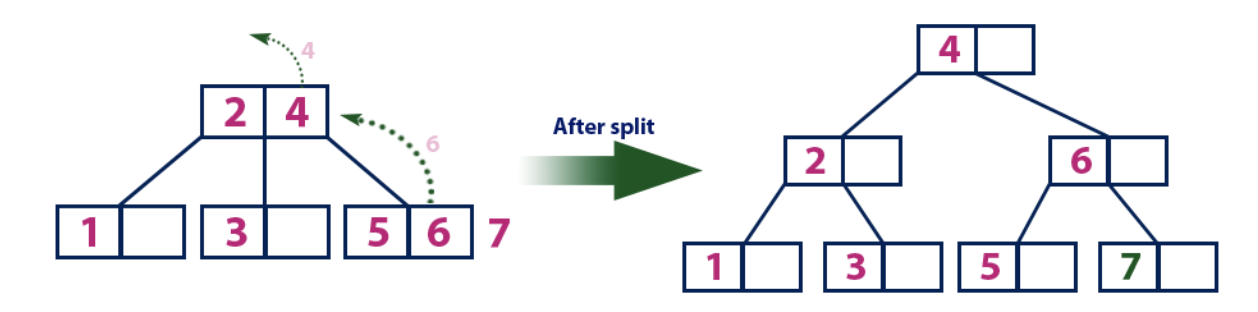
Insert(7):
Элемент «7» больше, чем элементы корня «2» и «4», который не является листом. Мы двигаемся по правому поддереву от элемента «4». Мы достигаем узла-листа и видим, что он полон. Мы делим этот узел, отправляя среднее значение «6» вверх к родительскому узлу с элементами «2» и «4». Однако родительский узел тоже полон, поэтому мы делим узел с элементами «2» и «4», отправляя значение «4» родительскому узлу. Только вот этого узла еще нет. В таком случае узел с элементом «4» становится новым корнем дерева.
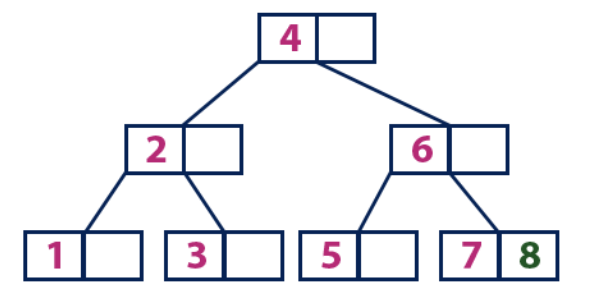
Insert(8):
Элемент «8» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значением «6». «8» больше «6» и узел с элементом «6» не является листом, поэтому двигаемся по правому поддереву от «6». Мы достигаем узла-листа с «7», у которого есть пустая ячейка, поэтому в нее мы помещаем «8».
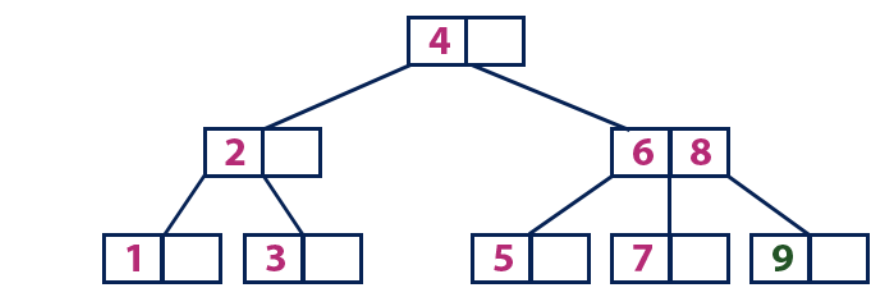
Insert(9):
Элемент «9» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значением «6». «9» больше «6» и узел с элементом «6» не является листом, поэтому двигаемся по правому поддереву от «6». Мы достигаем узла-листа со значениями «7» и «8». Он полон. Мы делим этот узел, отправляя среднее значение (8) родительскому узлу. Родительский узел «6» имеет пустую ячейку, поэтому мы помещаем «8» в нее. При этом новый элемент «9» добавляется в узел-лист.
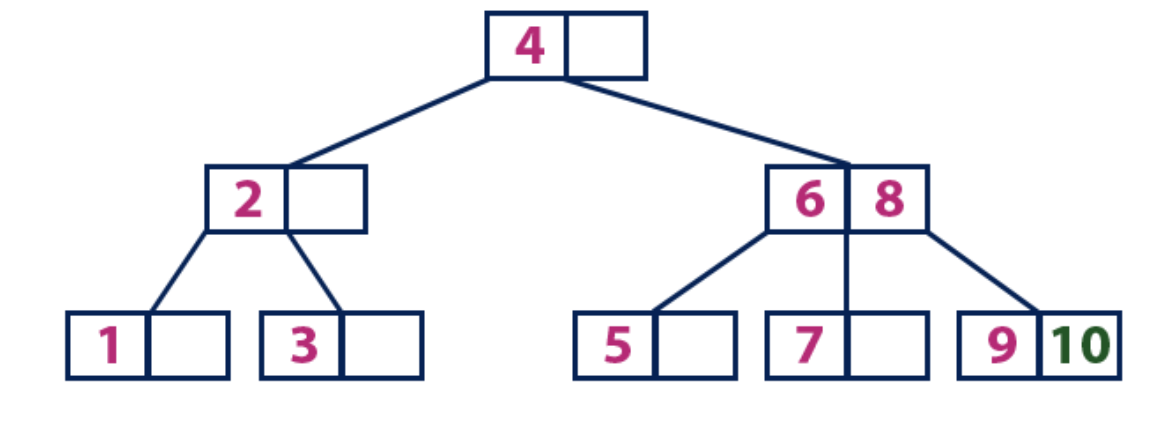
Insert(10):
Элемент «10» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значениями «6» и «8». «10» больше «6» и «8» и узел с этими элементами не является листом, поэтому двигаемся по правому поддереву от «8». Мы достигаем узла-листа со значением «9». У него есть пустая ячейка, поэтому туда мы помещаем «10».
Предлагаем вам самостоятельно на практике понять, как устроены В-деревья, воспользовавшись этой визуализацией.
Ждем всех на бесплатном открытом уроке, который пройдет уже 12 июля. До встречи!
Источник