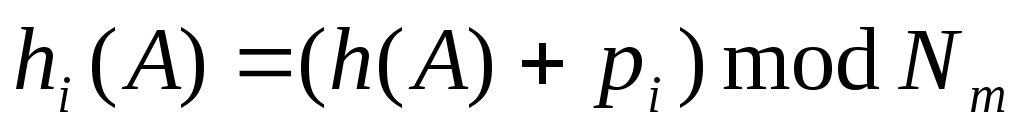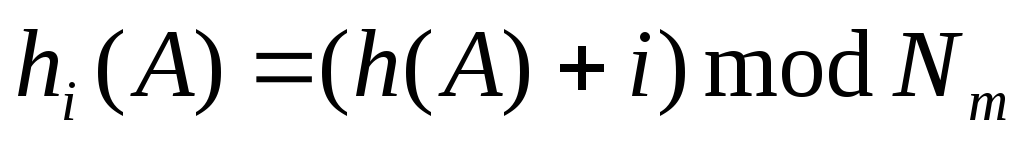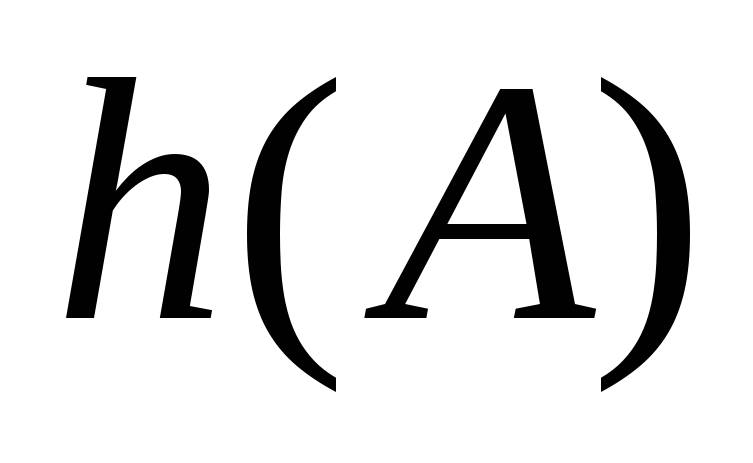Бинарные деревья блок схема

1.3 Метод бинарного дерева

Метод построения таблиц, при котором таблица имеет форму бинарного дерева. Каждый узел дерева представляет собой элемент таблицы, причем корневой узел является первым элементом. При построении дерева элементы сравниваются между собой, и в зависимости от результатов, выбирается путь в дереве. Предположим, что надо записать новый идентификатор. Для него выбирается левое поддерево, если этот идентификатор меньше текущего, если же идентификатор больше, выбирается правое поддерево. В случае если текущий узел не является концевым, переходим в следующий узел (согласно выбранному направлению) и опять сравниваем добавляемый идентификатор с текущим.

Для данного метода число требуемых сравнений и форма получившегося дерева во многом зависят от того порядка, в котором поступают идентификаторы.

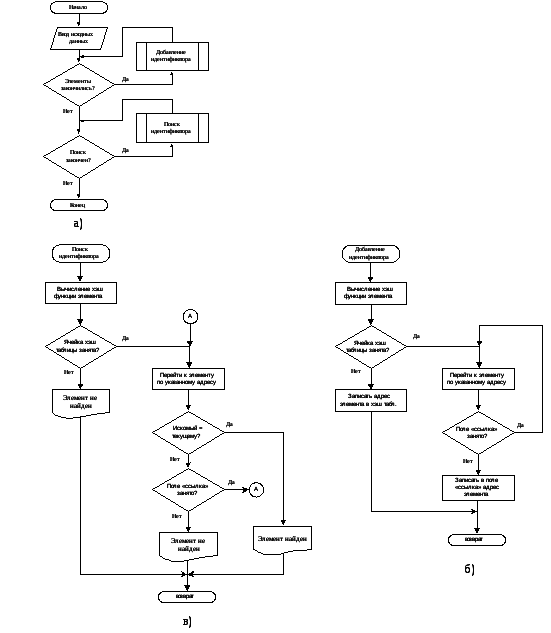
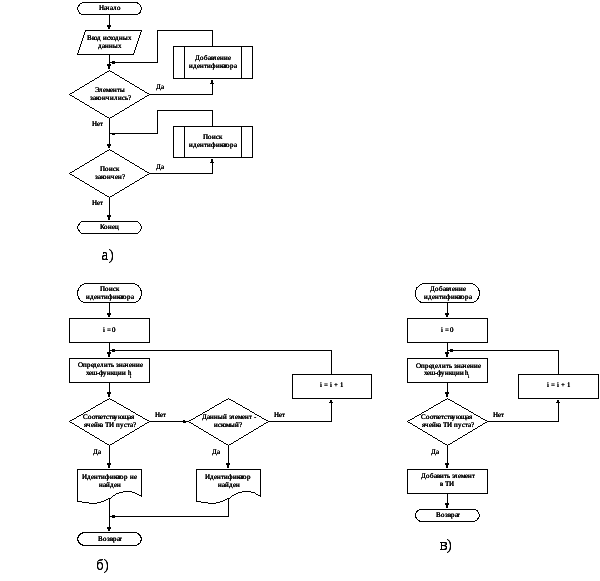
Блок-схема метода бинарного дерева представлена на рисунке 1.1

Рис. 1. 1 – Блок-схема метода бинарного дерева; а) – Блок-схема алгоритма метода бинарного дерева;б) – Блок-схема функции добавления идентификатора;

в) – Блок-схема функции поиска идентификатора

1.4 Метод цепочек

Блок-схема метода цепочек списка представлена на рисунке 1.2

Рис. 1.2 – Блок-схема метода цепочек; а) – Блок-схема алгоритма метод цепочек;

б) – Блок-схема функции добавление идентификатора;в) – Блок-схема функции поиска идентификатора

1.5 Результат выполнения программы

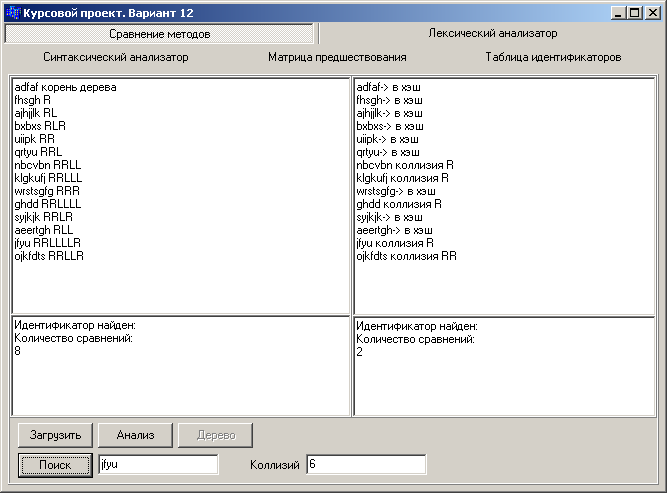
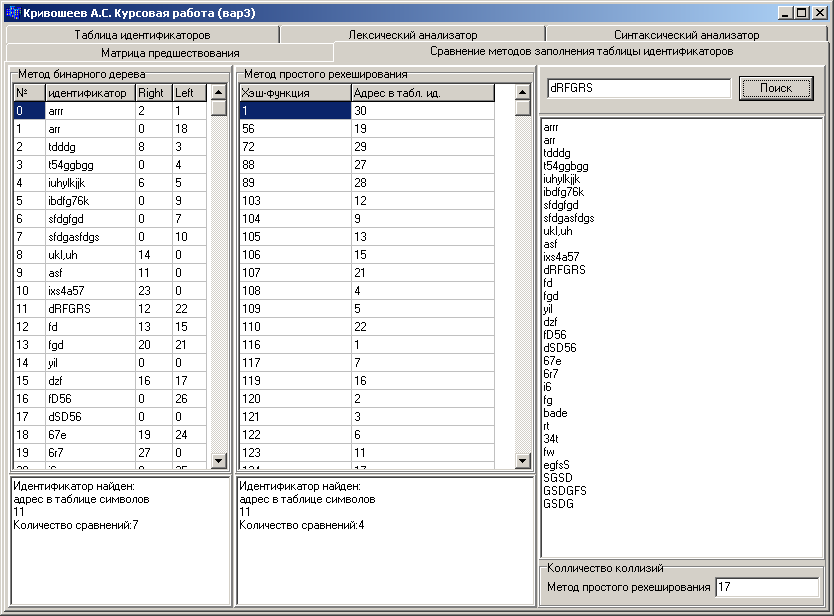
Рис. 1.3 – Результаты сравнения методов организации таблицы идентификаторов

При поиске идентификаторов в таблицах организованных методом бинарного дерева и методом цепочек было установлено, что количество сравнений в бинарном дереве в несколько раз больше, чем в методе цепочек.

Для сравнения методов организации таблицы идентификаторов был разработан модуль, иллюстрирующий их работу.

Было выявлено, что метод цепочек является более эффективным, чем метод бинарного дерева, так как для поиска идентификатора используется меньшее количество сравнений.

В дальнейшем для заполнения таблицы идентификаторов исходной программы будем использовать метод цепочек.

2 Проектирование лексического анализатора

Текст на входном языке задается в виде символьного (текстового) файла. Программа должна выдает сообщения о наличие во входном тексте ошибок, которые могут быть обнаружены на этапе лексического анализа.

Предусмотрены следующие варианты операторов входной про­граммы:

• оператор присваивания вида :=;
• условный оператор вида ifthen
• либо ifthenelse;
• составной оператор вида begin. end;
• оператор цикла dowhile;
• арифметические операции сложения (+), вычитания (-), декремент (—);
• операции сравнения «меньше» (<), «больше» (>), «равно» (=);
• логические операции and, or, not;
• операндами в выражениях могут выступать идентификаторы и константы;
• все идентификаторы должны воспри­ниматься как переменные целого типа.

2.2 Назначение лексического анализатора

Лексический анализатор (или сканер) – это часть компилятора, которая читает литеры программы на исходном языке и строит из них слова (лексемы) исходного языка. На вход лексического анализатора поступает текст исходной программы, а выходная информация передается для дальнейшей обработки компилятором на этапе синтаксического анализа и разбора. В основном лексические анализаторы выполняют исключение из текста исходной программы комментариев и незначащих пробелов, а также выделение лексем следующих типов: идентификаторов, строковых, символьных и числовых констант, ключевых (служебных) слов входного языка.

Источник

1.3 Метод простого рехэширования

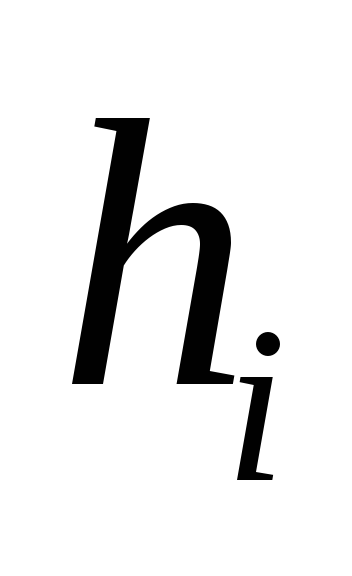
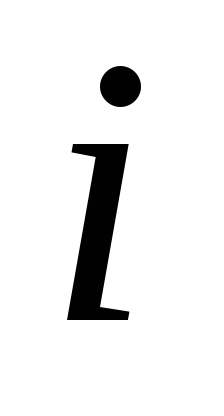
Для организации таблицы идентификаторов по методу рехэширования необходимо определить все хэш-функции для всехЧаще всего функцииопределяют как некоторую модификацию хэш-функцииh. Например, самым простым методом вычисления функцииявляется ее организация в виде



(1)

где — некоторое вычисляемое целое число, а— максимальное значение из области значений хэш-функцииh. В данной работе положим. Тогда получаем формулу



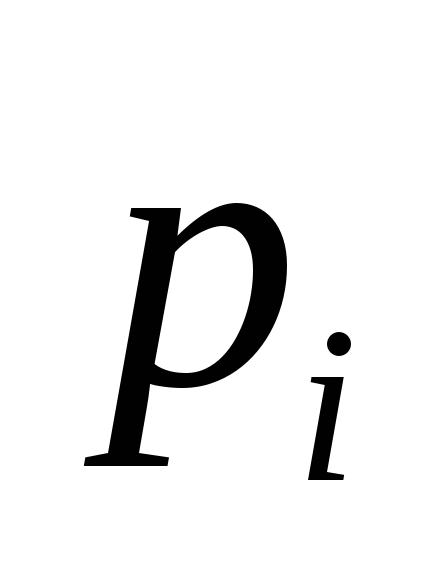
(2)



В этом случае при совпадении значений хэш-функции для каких-либо элементов поиск свободной ячейки в таблице начинается последовательно от текущей позиции, заданной хэш-функцией .

Блок-схема метода простого рехэширования представлена на рисунке 1.1.



Рис. 1.1 – Блок-схема метода простого рехэширования; а) – Блок-схема алгоритма простого рехэширования;б) – Блок-схема функции поиска идентификатора;

в) – Блок-схема функции добавления идентификатора

1.4 Метод бинарного дерева

Метод построения таблиц, при котором таблица имеет форму бинарного дерева. Каждый узел дерева представляет собой элемент таблицы, причем корневой узел является первым элементом. При построении дерева элементы сравниваются между собой, и в зависимости от результатов, выбирается путь в дереве. Предположим, что надо записать новый идентификатор. Для него выбирается левое поддерево, если этот идентификатор меньше текущего, если же идентификатор больше, выбирается правое поддерево. В случае если текущий узел не является концевым, переходим в следующий узел (согласно выбранному направлению) и опять сравниваем добавляемый идентификатор с текущим.

Для данного метода число требуемых сравнений и форма получившегося дерева во многом зависят от того порядка, в котором поступают идентификаторы.

Блок-схема метода бинарного дерева представлена на рисунке 1.2



Рис. 1. 1 – Блок-схема метода бинарного дерева; а) – Блок-схема алгоритма метода бинарного дерева;б) – Блок-схема функции добавления идентификатора;

в) – Блок-схема функции поиска идентификатора

1.5 Результат выполнения программы



Рис. 1.3 – Результаты сравнения методов организации таблицы идентификаторов

Для сравнения методов организации таблицы идентификаторов был разработан модуль, иллюстрирующий их работу.

Было выявлено, что для метода рехэширования для поиска идентификатора используется меньшее количество сравнений, чем для метода бинарного дерева.

В дальнейшем для заполнения таблицы идентификаторов исходной программы будем использовать метод бинарного дерева, т.к метод простого рехэширования требует больше памяти, и общее кол-во переменных зависит от длинны хэш-таблицы.

2 Проектирование лексического анализатора

2.1 Исходные данные

Текст на входном языке задается в виде символьного (текстового) файла. Программа должна выдает сообщения о наличие во входном тексте ошибок, которые могут быть обнаружены на этапе лексического анализа.

Предусмотрены следующие варианты операторов входной про­граммы:

условный оператор вида if then

составной оператор вида begin. end;

оператор цикла whiledo ;

операции сложения (+), вычитания (-), инкремент (++);

операции сравнения «меньше» (<), «больше» (>), «равно» (=);

логические операции and, or, not;

операндами в выражениях могут выступать идентификаторы и константы;

все идентификаторы должны воспри­ниматься как переменные.

Источник

Бинарные деревья. Процедуры, необходимые для работы с бинарными деревьями. Структура хранения бинарных деревьев



Дерево называется m-арным, если полустепень исхода для каждой его вершины не превышает m. При m равном двум имеет место бинарное дерево. Упорядоченные бинарные деревья называют также позиционными бинарными деревьями. Для вершин позиционного бинарного дерева естественно использовать термины «отец», «левое поддерево», «правое поддерево», «левый сын», «правый сын».

Префиксный код бинарного дерева.

Существует естественный способ описания (или идентификации) каждой вершины бинарного дерева с использованием двоичного алфавита. Корень характеризуется пустой строкой, а идентификатор любой другой вершины состоит из префикса, который является кодом отца и окончания, которое для левого сына является нулем, а для правого – единицей.

Префиксным кодом дерева называется множество строк, соответствующих листьям дерева. Это естественный способ отображения структуры бинарного дерева в памяти ЭВМ.

Процедуры, необходимые для работы с бинарными деревьями.

Набор процедур, необходимых для программной реализации структур типа позиционного бинарного дерева, должен обеспечить возможность реализации всех запросов, возникающих в различных приложениях. Практика выявила необходимость включения в такой набор следующих процедур:

Info(p) – возвращает содержимое узла по указателю р;

Left(p), right(p) – возвращают соответственно указатели на левого и правого сына вершины с адресом р;

Father(p) – возвращает указатель на отца заданного узла;

Brother(p) – возвращает указатель на брата заданной вершины;

Isleft(p), isright(p) – возвращает значение «истина», если р указывает на вершину соответственно с левым или правым сыном;

MakeTree(x) – возвращает указатель на корень вновь созданного дерева с информационным полем x в его корне;

Setleft(p,x), setright(p,x) – создают соответственно левого либо правого сына с заданным информационным полем и возвращают указатель на вновь созданную вершину.

Еще одна обычная операция – прохождение бинарного дерева. Очевидный порядок прохождения узлов линейного списка – от первого к последнему, либо наоборот. Для узлов дерева такого естественного порядка не существует. Поэтому прохождение дерева связано с некоторой целостной концепцией, которая обычно использует рекурсивную природу дерева.

Рассмотрим пример использования указанных выше процедур для формирования дерева по префиксному коду. Например, префиксный код может представлять собой множество:

Рассмотрим блок-схему алгоритма формирования бинарного дерева по префиксному коду с использованием перечисленных выше процедур. В блок-схеме используем следующие переменные:

s – идентификатор очередного листа;

s – фрагмент строки кода листа от первого символа до текущего символа включительно;

p – указатель на текущую вершину дерева;

l – длина кода обрабатываемого листа.

начало R_i=make tree (» «) ввод S return (R)

Источник

Читайте также:  Дерево целей предприятия экономической службы