Бинарные деревья и стеки

19.7. Очереди и стеки

Очередь и стек — это частные случаи однонаправленного списка. В стеке добавление и удаление элементов осуществляются с од­ ного конца, который называется вершиной стека, поэтому для стека можно определить функции: — top() — доступ к вершине стека (вывод значения последнего элемента; — рор() — удаление элемента из вершины (удаление последнего элемента); — push() — добавление элемента в вершину (добавление в конец). Такой принцип обслуживания называют LIFO (last in — first out, последний пришел, первый ушел). point* pop(point*beg) < point*p=beg; if (beg->next==0)//один элемент < delete beg; return 0; >//ищем предпоследний элемент while (p->next->next!=0) p=p->next; //ставим указатель г на последний элемент point*r=p->next; //обнуляем адресное поле предпоследнего элемента p->next=0;

delete г;//удаляем последний элемент return beg; > point* push(point* beg) < point*p=beg;//ставим указатель p на начало //списка point*q=new(point);//создаем новый элемент cout>q->data; q->next=0; if (beg==0)//список пустой < beg=q;//q становится первым элементом return beg; >while (p->next!=0)//проходим до конца списка p=p->next; p->next=q;//связываем последний элемент с q return beg; > В очереди добавление осуществляется в один конец, а удаление из другого конца. Такой принцип обслуживания называют FIFO (first in — first out, первый пришел, первый ушел). Для очереди также мож­ но определить функции: — front() — доступ к первому элементу; — back() — доступ к последнему элементу; — рор() — удаление элемента из конца; — pushO — добавление элемента в начало.

19.8. Бинарные деревья

Бинарное дерево — это динамическая структура данных, состоя­ щая из узлов, каждый из которых содержит кроме данных не более двух ссылок на другие бинарные деревья (поддеревья). На каждое поддерево имеется ровно одна ссылка (рис. 19).

Описать такую структуру можно следующим образом: struct point < int data;//информационное поле point* left;//адрес левого поддерева point* right;//адрес правого поддерева >; Рис. 19. Структура бинарного дерева Начальный узел называется конем дерева. Узел, не имеющий поддеревьев, называется листом дерева. Исходящие листы называют­ ся предками, входящие — потомками. Высота дерева определяется количеством уровней, на которых располагаются узлы. Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все клю­ чи его правого поддерева — больше, то оно называется деревом поис­ ка. Одинаковые ключи не допускаются. В дереве поиска можно най­ ти элемент по ключу, двигаясь от корня и переходя на левое или пра­ вое поддерево в зависимости от значения в каждом узле. Такой поиск является более эффективным, чем поиск по линейному списку, так как время поиска определяется высотой дерева, а она пропорцио­ нальна двоичному логарифму количества узлов (аналогично бинар­ ному поиску). В идеально сбалансированном дереве количество узлов справа и слева отличается не более чем на единицу.

Линейный список можно представить как вырожденное бинар­ ное дерево, в котором каждый узел имеет не более одной ссылки. Для списка среднее время поиска равно половине длины списка. Деревья и списки являются рекурсивными структурами данных, так как каждое поддерево также является деревом. Дерево можно опреде­ лить как рекурсивную структуру, в которой каждый элемент является: — либо пустой структурой; — либо элементом, с которым связано конечное число поддеревьев. Действия с рекурсивными структурами удобнее всего описыва­ ются с помощью рекурсивных алгоритмов.

19.9. Обход дерева

Для того чтобы выполнить определенную операцию над всем уз­ лами дерева, надо обойти все узлы. Такая задача называется обходом дерева. При обходе узлы должны посещаться в определенном поряд­ ке. Существуют три принципа упорядочивания, которые естественно вытекают из структуры дерева. Рассмотрим дерево (см. рис. 19). На этом дереве можно определить три метода упорядочения: 1) слева направо: Левое поддерево — Корень — Правое поддерево; 2) сверху вниз: Корень — Левое поддерево — Правое поддерево; 3) снизу вверх: Левое поддерево — Правое поддерево — Корень. Эти три метода можно сформулировать в виде рекурсивных ал­ горитмов. Эти алгоритмы служат примером того, что действия с ре­ курсивными структурами лучше всего описываются рекурсивными алгоритмами. //Обход слева направо: void Run(point*p) < if (Р) < Run(p->left); //переход к левому п/д собработка p->data> Run(p->right);//переход к правому п/д > >

Если в качестве операции обработки узла поставить операцию вывода информационного поля узла, то мы получим функцию для печати дерева. Для дерева поиска, изображенного на рис. 20, обход слева на­ право даст следующие результаты: 1 3 5 7 8 9 12. Рис. 20. Пример дерева поиска //Обход сверху вниз: void Run(point*p) < if (р) < собработка p->data> Run(p->left); //переход к левому п/д Run(p->right);//переход к правому п/д > > Результаты обхода слева направо для дерева поиска (см. рис. 20): 5 3 1 9 8 7 12. //Обход снизу вверх void Run(point*p) < if (Р)

Источник

Cтруктуры данных

Структура данных – это контейнер, который хранит информацию в определенном виде.

Из-за такой «компоновки» она может быть эффективной в одних операциях и неэффективной в других. Цель разработчика – выбрать из существующих структур оптимальный для конкретной задачи вариант.

Зачем нужны структуры данных?

Данные являются самой важной сущностью в информатике, а структуры позволяют хранить их в организованной форме.

В зависимости от ситуации данные должны храниться в некотором определенном формате. Структуры данных предлагают несколько вариантов таких размещений.

8 часто используемых структур

Часто используемые структуры данных:

• Массив (Array)
• Стек (Stack)
• Очередь (Queue)
• Связный список (Linked List)
• Дерево (Tree)
• Граф (Graph)
• Префиксное дерево (Trie)
• Хэш-Таблица (Hash Table)

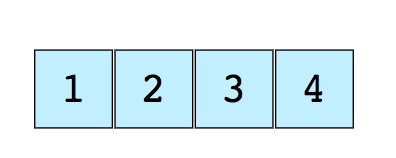
Массивы

Массив – это самая простая и наиболее широко используемая из структур. Стеки и очереди являются производными от массивов. Вот изображение простого массива размером 4, содержащего элементы (1, 2, 3 и 4).

Каждому из них присваивается неотрицательное числовое значение – индекс, который соответствует позиции этого элемента в массиве. Большинство языков определяют начальный индекс массива как 0.

Существует два типа массивов:

Основные операции с массивами

• Insert – вставка.
• Get – получение элемента.
• Delete – удаление.
• Size – получение общего количества элементов в массиве.

Частые вопросы о массивах

• Найти второй минимальный элемент.
• Первые не повторяющиеся целые числа.
• Объединить два отсортированных массива.
• Переставить положительные и отрицательные значения.

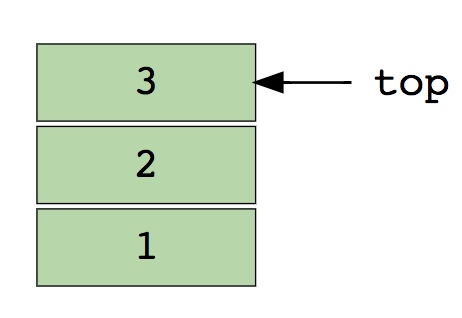
Стеки

Пример стека из реальной жизни – куча книг, лежащих друг на друге. Чтобы получить книгу, которая находится где-то в середине, вам нужно удалить все, что лежит сверху. Так работает метод LIFO (Last In First Out, последним пришел – первым ушел).

Вот изображение стека, содержащего три элемента (1, 2 и 3). Элемент 3 находится сверху и будет удален первым:

Основные операции со стеками

• Push – вставка элемента наверх стека.
• Pop – получение верхнего элемента и его удаление.
• isEmpty – возвращает true, если стек пуст.
• Top – получение верхнего элемента без удаления.

Часто задаваемые вопросы о стеках

• Вычисление постфиксного выражения с помощью стека.
• Сортировка значений в стеке.
• Проверка сбалансированности скобок в выражении.

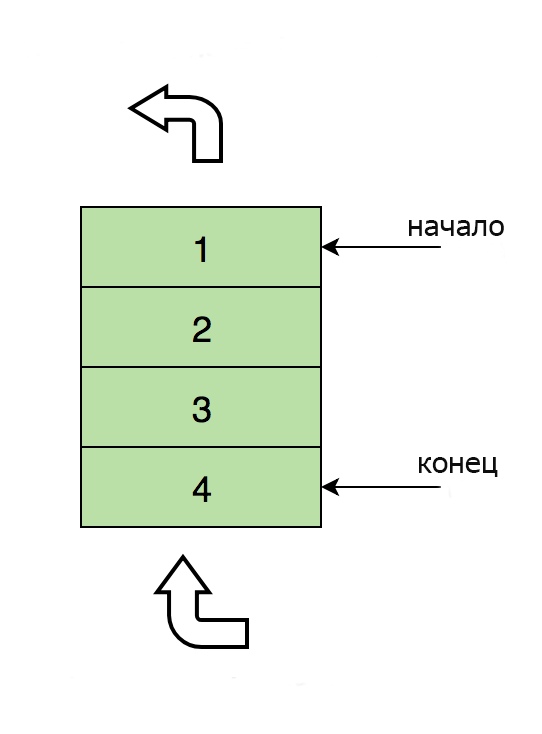
Очереди

Как и стек, очередь – это линейная структура данных, которая хранит элементы последовательно. Единственное существенное различие заключается в том, что вместо использования метода LIFO, очередь реализует метод FIFO (First in First Out, первым пришел – первым ушел).

Идеальный пример этих структур в реальной жизни – очереди людей в билетную кассу. Если придет новый человек, он присоединится к линии с конца, а не с начала. А человек, стоящий впереди, первым получит билет и, следовательно, покинет очередь.

Вот изображение очереди, содержащей четыре элемента (1, 2, 3 и 4). Здесь 1 находится вверху и будет удален первым:

Основные операции с очередями

• Enqueue – вставка в конец.
• Dequeue – удаление из начала.
• isEmpty – возвращает true, если очередь пуста.
• Top – получение первого элемента.

Часто задаваемые вопросы об очередях

• Реализация стека с помощью очереди.
• Развернуть первые k элементов.
• Генерация двоичных чисел от 1 до n с помощью очереди.

Связный список

Еще одна важная линейная структура данных, которая на первый взгляд похожа на массив, но отличается распределением памяти, внутренней организацией и способом выполнения основных операций вставки и удаления.

Связный список – это сеть узлов, каждый из которых содержит данные и указатель на следующий узел в цепочке. Также есть указатель на первый элемент – head. Если список пуст, то он указывает на null.

Связные списки используются для реализации файловых систем, хэш-таблиц и списков смежности.

Вот визуальное представление внутренней структуры связного списка:

Основные операции со связными списками

• InsertAtEnd – вставка в конец.
• InsertAtHead – вставка в начало.
• Delete – удаление указанного элемента.
• DeleteAtHead – удаление первого элемента.
• Search – получение указанного элемента.
• isEmpty – возвращает true, если связный список пуст.

Часто задаваемые вопросы о связных списках

• Разворот связного списка.
• Обнаружение цикла.
• Получение N-го узла с конца.
• Удаление дубликатов.

Графы

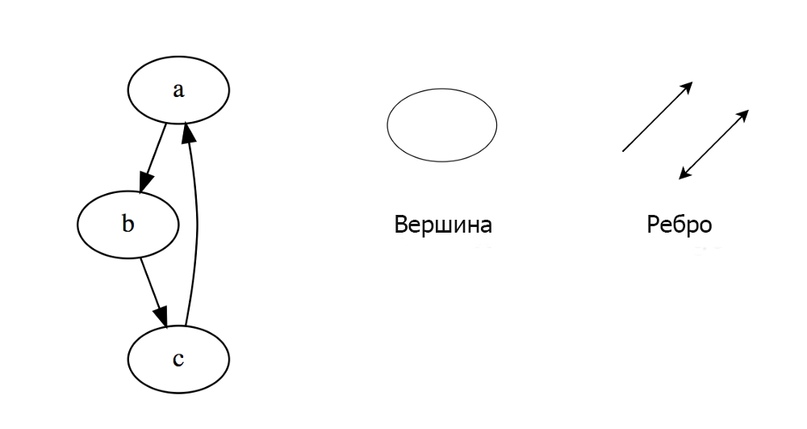
Граф представляет собой набор узлов, соединенных друг с другом в виде сети. Узлы также называются вершинами. Пара (x, y) называется ребром, которое указывает, что вершина xсоединена с вершиной y. Ребро может содержать вес/стоимость, показывая, сколько затрат требуется, чтобы пройти от x до y.

В языке программирования графы могут быть представлены в двух формах:

Общие алгоритмы обхода графов:

Часто задаваемые вопросы о графах

• Реализовать поиск по ширине и глубине.
• Проверка, является ли граф деревом.
• Количество ребер в графе.
• Кратчайший путь между двумя вершинами.

Деревья

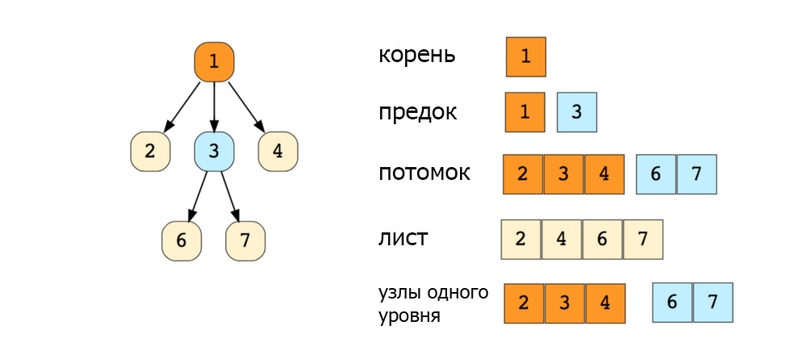
Дерево – это иерархическая структура данных, состоящая из вершин (узлов) и ребер, соединяющих их. Они похожи на графы, но есть одно важное отличие: в дереве не может быть цикла.

Деревья широко используются в искусственном интеллекте и сложных алгоритмах для обеспечения эффективного механизма хранения данных.

Вот изображение простого дерева, и основные термины:

• N-арное дерево;
• сбалансированное дерево;
• бинарное дерево;
• бинарное дерево поиска;
• дерево AVL;
• красно-чёрное дерево;
• 2-3 дерево.

Из всех типов чаще всего используются бинарное дерево и бинарное дерево поиска.

Часто задаваемые вопросы о деревьях

• Высота бинарного дерева.
• Найти k-ое максимальное значение в дереве бинарного поиска.
• Узлы на расстоянии k от корня.
• Предки заданного узла в бинарном дереве.

Префиксное дерево

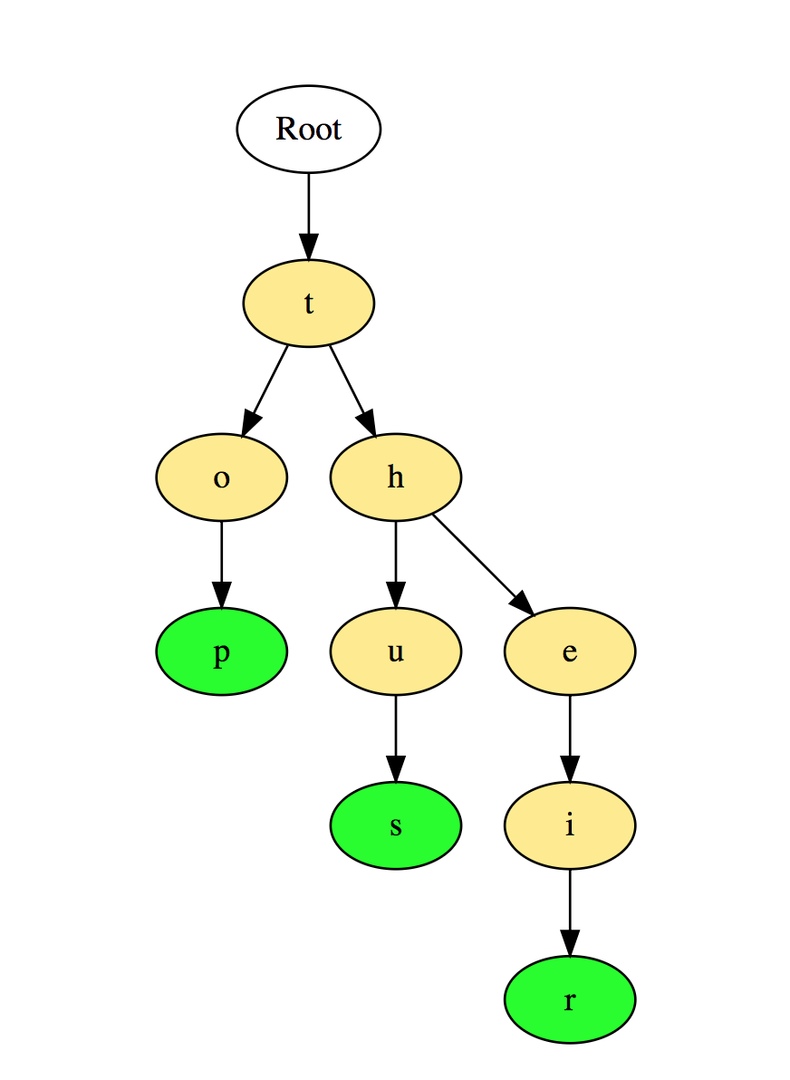
Префиксные деревья (tries) – древовидные структуры данных, эффективные для решения задач со строками. Они обеспечивают быстрый поиск и используются преимущественно для поиска слов в словаре, автодополнения в поисковых системах и даже для IP-маршрутизации.

Вот иллюстрация того, как три слова top, thus и their хранятся в префиксном дереве:

Слова размещаются сверху вниз. Выделенные зеленым элементы показывают конец каждого слова.

Часто задаваемые вопросы о префиксных деревьях

• Общее количество слов.
• Вывод всех слов.
• Сортировка элементов массива.
• Формирование слов из словаря.
• Создание словаря T9.

Хеш-Таблица

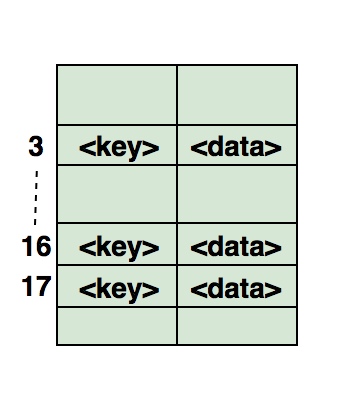
Хеширование – это процесс, используемый для уникальной идентификации объектов и хранения каждого из них в некотором предварительно вычисленном уникальном индексе – ключе. Итак, объект хранится в виде пары ключ-значение, а коллекция таких элементов называется словарем. Каждый объект можно найти с помощью его ключа. Существует несколько структур, основанных на хешировании, но наиболее часто используется хеш-таблица, которая обычно реализуется с помощью массивов.

Производительность структуры зависит от трех факторов:

Вот иллюстрация того, как хэш отображается в массиве. Индекс вычисляется с помощью хеш-функции.

• Часто задаваемые вопросы о хеш-таблицах
• Найти симметричные пары.
• Определить, является ли массив подмножеством другого массива.
• Проверить, являются ли массивы непересекающимися.

Источник