Алгоритмы поиска на основе деревьев
Аннотация: В лекции рассматриваются определение и виды деревьев поиска, приемы снижения трудоемкости поиска в древовидных структурах, приводятся описания алгоритмов поиска в двоичных упорядоченных, случайных и сбалансированных в высоту (АВЛ) деревьях, приводятся примеры программной реализации бинарного дерева поиска и АВЛ-дерева.
Цель лекции: изучить алгоритмы поиска на основе деревьев, научиться решать задачи поиска через построение упорядоченного, случайного, оптимального или сбалансированного в высоту деревьев на языке C++.
Поиск данных, являясь одним из приоритетных направлений работы с данными, предполагает использование соответствующих алгоритмов в зависимости от ряда факторов: способ представления данных, упорядоченность множества поиска, объем данных, расположение их во внешней или во внутренней памяти. Поиск – процесс нахождения конкретной информации в ранее созданном множестве данных. Как правило, данные представляют собой структуры, каждая из которых имеет хотя бы один ключ – значение определенного поля конкретной структуры. Ключ поиска – это поле , по значению которого происходит поиск .
Рассмотрим организацию поиска данных, имеющих древовидную структуру. Анализируя дерево только с точки зрения представления данных в виде иерархической структуры, заметим, что выигрыша при организации поиска не получится. Сравнение ключа поиска с эталоном необходимо провести для всех элементов дерева.
Уменьшить число сравнений ключей с эталоном возможно, если выполнить организацию дерева особым образом, то есть расположить его элементы по определенным правилам. При этом в процессе поиска будет просмотрено не все дерево , а отдельное поддерево . Такой подход позволяет классифицировать деревья в зависимости от правил построения. Выделим некоторые популярные виды деревьев, на основе которых рассмотрим организацию поиска.
Двоичные (бинарные) деревья
Двоичные деревья представляют собой иерархическую структуру, в которой каждый узел имеет не более двух потомков. То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). При этом каждое поддерево в свою очередь тоже является деревом. Поиск на таких структурах не дает выигрыша по выполнению по сравнению с линейными структурами того же размера, так как необходимо в худшем случае выполнить обход всего дерева. Поэтому интерес представляют двоичные упорядоченные деревья.
Двоичные упорядоченные деревья
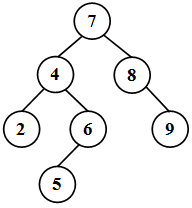
Двоичное дерево упорядоченно, если для любой его вершины x справедливы такие свойства ( рис. 40.1):
- все элементы в левом поддереве меньше элемента, хранимого в x ,
- все элементы в правом поддереве больше элемента, хранимого в x ,
- все элементы дерева различны.
Если в дереве выполняются первые два свойства, но встречаются одинаковые элементы, то такое дерево является частично упорядоченным. В дальнейшем будет идти речь только о двоичных упорядоченных деревьях. Основными операциями, производимыми с упорядоченным деревом, являются:
- поиск вершины;
- добавление вершины;
- удаление вершины ;
- вывод (печать) дерева;
- очистка дерева.
Пример 1. Программная реализация основных операций бинарного дерева поиска.
#include «stdafx.h» #include #include using namespace std; typedef int T; // тип элемента #define compLT(a,b) (a < b) #define compEQ(a,b) (a == b) typedef struct Node_ < T data; // значение узла struct Node_ *left;// левый потомок struct Node_ *right;// правый потомок struct Node_ *parent;// родитель >Node; Node *root = NULL; //корень бинарного дерева поиска Node* insertNode(T data); void deleteNode(Node *z); Node* findNode(T data); void printTree(Node *node, int l = 0); int _tmain(int argc, _TCHAR* argv[])< int i, *a, maxnum; cout > maxnum; cout cout = 0; i—) < findNode(a[i]); >// очистка бинарного дерева поиска for (i = 0; i < maxnum; i++) < deleteNode(findNode(a[i])); >system(«pause»); return 0; > //функция выделения памяти для нового узла и вставка в дерево Node* insertNode(T data) < Node *x, *current, *parent; current = root; parent = 0; while (current) < if ( data == current->data ) return (current); parent = current; current = data < current->data ? current->left : current->right; > x = new Node; x->data = data; x->parent = parent; x->left = NULL; x->right = NULL; if(parent) if( x->data < parent->data ) parent->left = x; else parent->right = x; else root = x; return(x); > //функция удаления узла из дерева void deleteNode(Node *z) < Node *x, *y; if (!z || z == NULL) return; if (z->left == NULL || z->right == NULL) y = z; else < y = z->right; while (y->left != NULL) y = y->left; > if (y->left != NULL) x = y->left; else x = y->right; if (x) x->parent = y->parent; if (y->parent) if (y == y->parent->left) y->parent->left = x; else y->parent->right = x; else root = x; if (y != z) < y->left = z->left; if (y->left) y->left->parent = y; y->right = z->right; if (y->right) y->right->parent = y; y->parent = z->parent; if (z->parent) if (z == z->parent->left) z->parent->left = y; else z->parent->right = y; else root = y; free (z); > else < free (y); >> //функция поиска узла, содержащего data Node* findNode(T data) < Node *current = root; while(current != NULL) if(compEQ(data, current->data)) return (current); else current = compLT(data, current->data) ? current->left : current->right; return(0); > //функция вывода бинарного дерева поиска void printTree(Node *node, int l)< int i; if (node != NULL) < printTree(node->right, l+1); for (i=0; i < l; i++) cout data); printTree(node->left, l+1); > else cout
Алгоритм удаления элемента более трудоемкий, так как надо соблюдать упорядоченность дерева. При удалении может случиться, что удаляемый элемент находится не в листе, то есть вершина имеет ссылки на реально существующие поддеревья . Эти поддеревья терять нельзя, а присоединить два поддерева на одно освободившееся после удаления место невозможно. Поэтому необходимо поместить на освободившееся место либо самый правый элемент из левого поддерева , либо самый левый из правого поддерева . Упорядоченность дерева при этом не нарушится. Удобно придерживаться одной стратегии, например, заменять самый левый элемент из правого поддерева . Нельзя забывать, что при замене вершина , на которую производится замена, может иметь правое поддерево . Это поддерево необходимо поставить вместо перемещаемой вершины.
Временная сложность этих алгоритмов (она одинакова для этих алгоритмов, так как в их основе лежит поиск ) оценим для наилучшего и наихудшего случая. В лучшем случае, то есть случае полного двоичного дерева , получаем сложность Omin(log n) . В худшем случае дерево может выродиться в список . Такое может произойти, например, при добавлении элементов в порядке возрастания. При работе со списком в среднем придется просмотреть половину списка. Это даст сложность Omax(n) .
Случайные деревья
Случайные деревья поиска представляют собой упорядоченные бинарные деревья поиска, при создании которых элементы (их ключи) вставляются в случайном порядке.
При создании таких деревьев используется тот же алгоритм , что и при добавлении вершины в бинарное дерево поиска. Будет ли созданное дерево случайным или нет, зависит от того, в каком порядке поступают элементы для добавления. Примеры различных деревьев, создаваемых при различном порядке поступления элементов, приведены ниже ( рис. 40.2).
При поступлении элементов в случайном порядке получаем дерево с минимальной высотой h (рис. 40.2А), при этом минимизируется время поиска элемента в дереве, которое пропорционально O(log n) . При поступлении элементов в упорядоченном виде (рис. 40.2В) или в порядке с единичными сериями монотонности (рис. 40.2С) происходит построение вырожденных деревьев поиска (оно вырождено в линейный список ), что нисколько не сокращает время поиска, которое составляет O(n) .
Источник