Бинарное дерево — что это? B-деревья
Статья расскажет о том, что такое бинарные деревья. Будут представлены способы их представления и основные термины. Отдельное внимание будет уделено B-дереву и его отличию от двоичных структур.
Деревом называют структуру данных, которая имеет древовидный вид, то есть характеризуется наличием набора связанных узлов. Бинарное дерево — это конечное множество элементов, связанных с двумя разными бинарными деревьями — правым и левым поддеревьями.
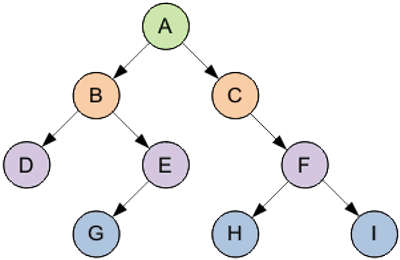
На что следует обратить внимание: — А — корень дерева; — B — корень левого поддерева и предок D; — С — корень правого поддерева; — D — потомок родительского узла B; если D располагается на уровне i, то B – на уровне i-1.
Необходимо выделить следующие термины: — узел (вершина) — это каждый элемент бинарного дерева; — ветви — связи между узлами; — глубина (высота) — наибольший уровень какого-нибудь элемента; — лист (терминальный узел) — термин применяется, если элемент не имеет потомков; — внутренние узлы — узлы ветвления; — степень внутреннего узла — число его потомков (наибольшая степень всех существующих узлов — это степень всего бинарного дерева); — длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути, которая равна i.
Использование
На практике бинарные деревья применяются, когда в каждой точке какого-нибудь вычислительного процесса нужно принимать одно из 2-х возможных решений. Существует множество задач, решаемых таким способом. Одна из них — выполнение операции, условно говоря, X с каждым элементом дерева. X рассматривается в качестве параметра обобщенной задачи посещения всех вершин либо задачи обхода дерева. Если рассмотреть такую задачу в качестве единого последовательного процесса, то можно сказать, что отдельные вершины посещаются в определенном порядке, то есть могут считаться линейно расположенными.
Способы обхода
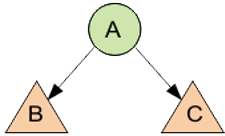
Предположим, что имеется дерево (не пустое), в котором A является корнем, а B и C — левым и правым поддеревьями.
Есть 3 способа обхода: 1. Обход в прямом порядке — сверху вниз: A, B, C — префиксная форма. 2. Обход слева направо (симметричный порядок): B, A, C — инфиксная форма. 3. Обход снизу вверх (обратный порядок): B, C, A — постфиксная форма.
Реализация
На практике вершину древа можно описать в качестве структуры:
Тогда обход в префиксной форме будет выглядеть следующим образом:
Бинарное дерево поиска
Оно представляет собой двоичное (бинарное) дерево, для которого справедлив ряд дополнительных условий. Эти условия называют свойствами:
Данные в каждой вершине должны обладать ключами, где определена операция сравнения “
Обычно информация, которая представляет каждую вершину, — это запись, а не единственное поле данных.
Чтобы составить бинарное дерево поиска, пригодится функция добавления узла:
Удаляем поддерево
B-дерево. Поиск по B-дереву
В бинарном дереве поиска каждый узел содержит лишь одно значение (ключ) и не более 2-х потомков. Но существует особый вид древа поиска, называемый B-дерево (Би-дерево). Здесь узел содержит больше одного значения и больше 2-х потомков. Также его называют сбалансированным по высоте деревом поиска порядка m (Height Balanced m-way Search Tree).
B-дерево представляет собой сбалансированное дерево поиска, где каждый узел содержит много ключей и имеет больше 2-х потомков.
Возможные операции: 1. Поиск. 2. Вставка (вставляем новый элемент). 3. Удаление.
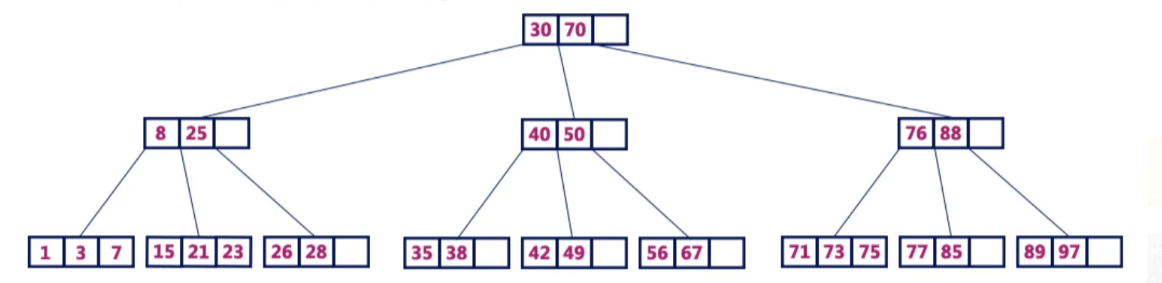
Каждое B-дерево имеет порядок. Для примера рассмотрим B-дерево порядка m. Оно будет обладать рядом следующих характеристик:
Ниже можно посмотреть на B-дерево четвертого порядка, содержащее максимум три значения ключа и максимум четыре потомка для каждой вершины.
Поиск аналогичен поиску по двоичному дереву. Следует вспомнить, что в двоичном древе поиск начинается с корня, причем каждый раз принимается 2-стороннее решение (пойти по правому поддереву либо по левому). В В-дереве поиск тоже начинается с корневого узла, но с той лишь разницей, что на каждом шаге принимается не 2-стороннее, а n-стороннее решение, причем n для дерева в данном случае представляет общее число потомков рассматриваемого узла. Сложность поиска такого дерева — O(log n).
Также существует такое понятие, как вставка в B-дерево.
В В-дереве вставка нового элемента возможна лишь в узел-лист. То есть вставленная новая пара ключ-значение добавляется лишь к узлу-листу. Вот, как осуществляется вставка в B-дерево:
Более подробную информацию всегда можно получить на наших курсах по алгоритмам в Москве:
Источник
Дерево
Дерево – структура данных, представляющая собой древовидную структуру в виде набора связанных узлов.
Бинарное дерево — это конечное множество элементов, которое либо пусто, либо содержит элемент ( корень ), связанный с двумя различными бинарными деревьями, называемыми левым и правым поддеревьями . Каждый элемент бинарного дерева называется узлом . Связи между узлами дерева называются его ветвями .
Способ представления бинарного дерева:
Корень дерева расположен на уровне с минимальным значением.
Узел D , который находится непосредственно под узлом B , называется потомком B . Если D находится на уровне i , то B – на уровне i-1 . Узел B называется предком D .
Максимальный уровень какого-либо элемента дерева называется его глубиной или высотой .
Если элемент не имеет потомков, он называется листом или терминальным узлом дерева.
Остальные элементы – внутренние узлы (узлы ветвления).
Число потомков внутреннего узла называется его степенью . Максимальная степень всех узлов есть степень дерева.
Число ветвей, которое нужно пройти от корня к узлу x , называется длиной пути к x . Корень имеет длину пути равную 0 ; узел на уровне i имеет длину пути равную i .
Бинарное дерево применяется в тех случаях, когда в каждой точке вычислительного процесса должно быть принято одно из двух возможных решений.
Имеется много задач, которые можно выполнять на дереве.
Распространенная задача — выполнение заданной операции p с каждым элементом дерева. Здесь p рассматривается как параметр более общей задачи посещения всех узлов или задачи обхода дерева.
Если рассматривать задачу как единый последовательный процесс, то отдельные узлы посещаются в определенном порядке и могут считаться расположенными линейно.
Способы обхода дерева
Пусть имеем дерево, где A — корень, B и C — левое и правое поддеревья.
Существует три способа обхода дерева:
- Обход дерева сверху вниз (в прямом порядке): A, B, C — префиксная форма.
- Обход дерева в симметричном порядке (слева направо): B, A, C — инфиксная форма.
- Обход дерева в обратном порядке (снизу вверх): B, C, A — постфиксная форма.
Реализация дерева
Узел дерева можно описать как структуру:
struct tnode <
int field; // поле данных
struct tnode *left; // левый потомок
struct tnode *right; // правый потомок
>;
При этом обход дерева в префиксной форме будет иметь вид
void treeprint(tnode *tree) <
if (tree!= NULL ) < //Пока не встретится пустой узел
cout field; //Отображаем корень дерева
treeprint(tree->left); //Рекурсивная функция для левого поддерева
treeprint(tree->right); //Рекурсивная функция для правого поддерева
>
>
Обход дерева в инфиксной форме будет иметь вид
void treeprint(tnode *tree) <
if (tree!= NULL ) < //Пока не встретится пустой узел
treeprint(tree->left); //Рекурсивная функция для левого поддерева
cout field; //Отображаем корень дерева
treeprint(tree->right); //Рекурсивная функция для правого поддерева
>
>
Обход дерева в постфиксной форме будет иметь вид
void treeprint(tnode *tree) <
if (tree!= NULL ) < //Пока не встретится пустой узел
treeprint(tree->left); //Рекурсивная функция для левого поддерева
treeprint(tree->right); //Рекурсивная функция для правого поддерева
cout field; //Отображаем корень дерева
>
>
Бинарное (двоичное) дерево поиска – это бинарное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):
- оба поддерева – левое и правое, являются двоичными деревьями поиска;
- у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, чем значение ключа данных самого узла X ;
- у всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, чем значение ключа данных узла X .
Данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.
Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных.
Для составления бинарного дерева поиска рассмотрим функцию добавления узла в дерево.
Добавление узлов в дерево
struct tnode * addnode( int x, tnode *tree) <
if (tree == NULL ) < // Если дерева нет, то формируем корень
tree = new tnode; // память под узел
tree->field = x; // поле данных
tree->left = NULL ;
tree->right = NULL ; // ветви инициализируем пустотой
> else if (x < tree->field) // условие добавление левого потомка
tree->left = addnode(x,tree->left);
else // условие добавление правого потомка
tree->right = addnode(x,tree->right);
return (tree);
>
Удаление поддерева
void freemem(tnode *tree) <
if (tree!= NULL ) <
freemem(tree->left);
freemem(tree->right);
delete tree;
>
>
Пример Написать программу, подсчитывающую частоту встречаемости слов входного потока.
Поскольку список слов заранее не известен, мы не можем предварительно упорядочить его. Неразумно пользоваться линейным поиском каждого полученного слова, чтобы определять, встречалось оно ранее или нет, т.к. в этом случае программа работает слишком медленно.
Один из способов — постоянно поддерживать упорядоченность уже полученных слов, помещая каждое новое слово в такое место, чтобы не нарушалась имеющаяся упорядоченность. Воспользуемся бинарным деревом.
В дереве каждый узел содержит:
- указатель на текст слова;
- счетчик числа встречаемости;
- указатель на левого потомка;
- указатель на правого потомка.
Рассмотрим выполнение программы на примере фразы
now is the time for all good men to come to the aid of their party
При этом дерево будет иметь следующий вид
#include
#include
#include
#include
//#include
#define MAX WORD 100
struct tnode < // узел дерева
char * word; // указатель на строку (слово)
int count; // число вхождений
struct tnode* left; // левый потомок
struct tnode* right; // правый потомок
>;
// Функция добавления узла к дереву
struct tnode* addtree( struct tnode* p, char * w) int cond;
if (p == NULL ) p = ( struct tnode*)malloc( sizeof ( struct tnode));
p->word = _strdup(w);
p->count = 1;
p->left = p->right = NULL ;
>
else if ((cond = strcmp(w, p->word)) == 0)
p->count++;
else if (cond < 0)
p->left = addtree(p->left, w);
else
p->right = addtree(p->right, w);
return p;
>
// Функция удаления поддерева
void freemem(tnode* tree) if (tree != NULL ) freemem(tree->left);
freemem(tree->right);
free(tree->word);
free(tree);
>
>
// Функция вывода дерева
void treeprint( struct tnode* p) if (p != NULL ) treeprint(p->left);
printf( «%d %s\n» , p->count, p->word);
treeprint(p->right);
>
>
int main() struct tnode* root;
char word[MAX WORD ];
root = NULL ;
do scanf_s( «%s» , word, MAX WORD );
if (isalpha(word[0]))
root = addtree(root, word);
> while (word[0] != ‘0’ ); // условие выхода – ввод символа ‘0’
treeprint(root);
freemem(root);
getchar();
getchar();
return 0;
>
Результат выполнения
Комментариев к записи: 19
Источник