Чем хороши красно черные деревья

14 Красно-чёрные деревья

В главе 13 мы показали, что основные операции с двоичным деревом поиска высоты h могут быть выполнены за O(h) действий. Деревья эффективны, если их высота мала. Но малая высота не гарантируется, и в худшем случае деревья не более эффективны, чем списки. Красно-чёрные деревья — один из «сбалансированных» деревьев поиска; специальные операции балансировки гарантируют, что высота дерева не превзойдёт O(logn).

14.1. Свойства красно-чёрных деревьев

Красно-чёрное дерево (red-black tree) — это двоичное дерево поиска, шины которого разделены на красные (red) и чёрные (black). Таким образом, каждая вершина хранит один дополнительный бит — её цвет.

При этом должны выполняться определённые требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в два раза поэтому дерево можно назвать сбалансированным (balanced).

Каждая вершина красно-чёрного дерева имеет поля color (цвет), key (ключ) left (левый ребёнок), right (правый ребёнок) и р (родитель). Если у вершины отсутствует ребёнок или родитель, соответствующее поле содержит NIL, для удобства мы будем считать, что значения nil, хранящиеся в полях left и являются ссылками на дополнительные (фиктивные) листья дерева. В таком пополненном дереве каждая старая вершина (содержащая ключ) имеет детей, и тем самым становится внутренней вершиной.

Двоичное дерево поиска называется красно-чёрным деревом, если оно дает следующими свойствами (будем называть их RB-свойствами, по-английс red-black properties):

1. каждая вершина — либо красная, либо чёрная;
2. каждый лист (nil) — чёрный;
3. если вершина красная, оба её ребёнка чёрные;
4. все пути, идущие вниз от корня к листьям, содержат одинаковое количество чёрных вершин.

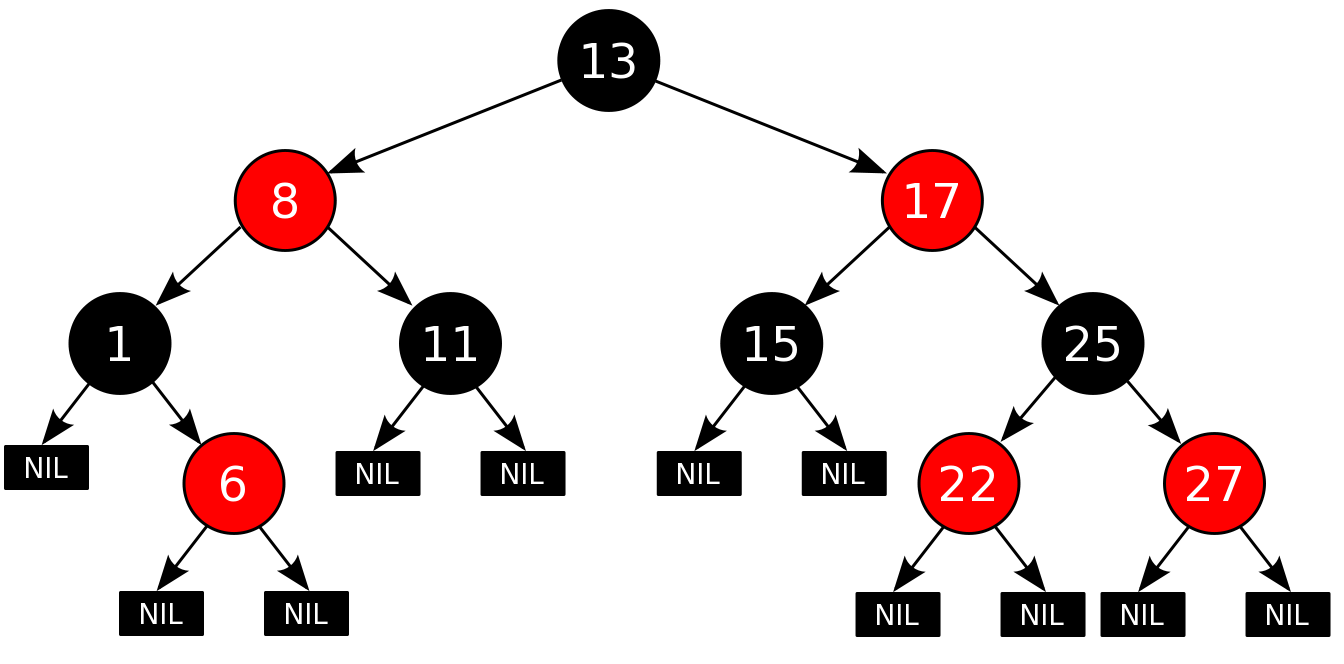
Пример красно-чёрного дерева показан на рис. 14.1. Рис. 14.1. Красно-чёрное дерево. Чёрные вершины показаны как тёмные, красные как серые. Каждая вершина либо красная, либо черная. Все nil-листья чёрные. Дети красной вершины — чёрные. Для каждой вершины все пути от неё вниз к листьям содержат одинаковое количество чёрных вершин. Около каждой вершины (кроме листьев) записана её чёрная высота. Чёрная высота листьев равна 0. Рассмотрим произвольную вершину х красно-чёрного дерева и пути, ве­дущие вниз от неё к листьям. Все они содержат одно и то же число чёрных вершин (добавим к ним путь из корня в х и применим свойство 4). Число чёрных вершин в любом из них (саму вершину х мы не считаем) будем называть чёрнойвысотой (black-height) вершины х и обозначать bh(ж). Чёрной высотой дерева будем считать чёрную высоту его корня. Следующая лемма показывает, что красно-чёрные деревья хороши как де­ревья поиска. Лемма 14.1.Красно-чёрное дерево с п внутренними вершинами (т. е. не считаяNIL-листъев) имеет высоту не больше 21og(n + l). Доказательство. Сначала покажем, что поддерево с корнем в х содержит по меньшей мере 2 bh ( x ) — 1 внутренних вершин. Доказательство проведём индукци­ей от листьев к корню. Для листьев чёрная высота равна 0, и поддерево в самом деле содержит не менее 2 bh ( x ) — 1 = 2° — 1 — 0 внутренних вершин. Пусть теперь вершина х не является листом и имеет чёрную высоту k. Тогда оба её ребёнка имеют чёрную высоту не меньше k— 1 (красный ребёнок будет иметь высоту А:, чёрный — k— 1). По предположению индукции левое и правое поддеревья вер­шины х содержат не менее 2 k -1 — 1 вершин, и потому поддерево с корнем в х содержит по меньшей мере 2k-1 — 1 + 2 k -1 — 1 + 1 = 2 k — 1 внутренних вершин. Чтобы завершить доказательство леммы, обозначим высоту дерева через h. Согласно свойству 3, по меньшей мере половину всех вершин на пути от корня к листу, не считая корень, составляют чёрные вершины. Следовательно, чёрная высота дерева не меньше h/2. Тогда Перенесём 1 налево и перейдём к логарифмам. Получим log(n + 1)h/2, или 2log(n + 1)h Тем самым для красно-чёрных деревьев операции search, minimum, successor и predecessor выполняются за время O(logn), так как их выполнения есть O(h) для дерева высоты h, а красно-чёрное дерево с n шинами имеет высоту О (log n). Сложнее обстоит дело с процедурами TREE-INSERT и TREE-DELETE из главы 13: проблема в том, что они могут испортить структуру красно-чёрного дерева, нарушив RB-свойства. Поэтому эти процедуры придется модифицировать. Мы увидим в разделах 14.3 и 14.4, как можно реализовать добавление, удаление элементов за время O(logn) с сохранением RB-свойств.

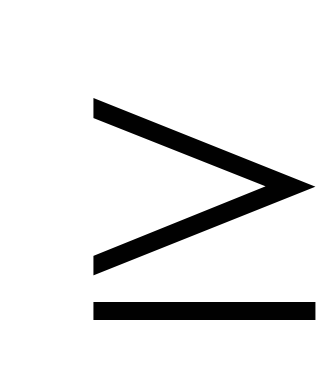
Источник

Красно-черные деревья: коротко и ясно

Итак, сегодня хочу немного рассказать о красно-черных деревьях. Рассказ будет кратким, без рассмотрения алгоритмов балансировки при вставке/удалении элементов в красно-черных деревьях.

Красно-черные деревья относятся к сбалансированным бинарным деревьям поиска.

Как бинарное дерево, красно-черное обладает свойствами:

1) Оба поддерева являются бинарными деревьями поиска.

2) Для каждого узла с ключом выполняется критерий упорядочения:

ключи всех левых потомков

(в других определениях дубликаты должны располагаться с правой стороны либо вообще отсутствовать).
Это неравенство должно быть истинным для всех потомков узла, а не только его дочерних узлов.

Свойства красно-черных деревьев:

1) Каждый узел окрашен либо в красный, либо в черный цвет (в структуре данных узла появляется дополнительное поле – бит цвета).

2) Корень окрашен в черный цвет.

3) Листья(так называемые NULL-узлы) окрашены в черный цвет.

4) Каждый красный узел должен иметь два черных дочерних узла. Нужно отметить, что у черного узла могут быть черные дочерние узлы. Красные узлы в качестве дочерних могут иметь только черные.

5) Пути от узла к его листьям должны содержать одинаковое количество черных узлов(это черная высота).

Ну и почему такое дерево является сбалансированным?

Действительно, красно-черные деревья не гарантируют строгой сбалансированности (разница высот двух поддеревьев любого узла не должна превышать 1), как в АВЛ-деревьях. Но соблюдение свойств красно-черного дерева позволяет обеспечить выполнение операций вставки, удаления и выборки за время . И сейчас посмотрим, действительно ли это так.

Пусть у нас есть красно-черное дерево. Черная высота равна (black height).

Если путь от корневого узла до листового содержит минимальное количество красных узлов (т.е. ноль), значит этот путь равен .

Если же путь содержит максимальное количество красных узлов ( в соответствии со свойством ), то этот путь будет равен .

То есть, пути из корня к листьям могут различаться не более, чем вдвое (, где h — высота поддерева), этого достаточно, чтобы время выполнения операций в таком дереве было

Как производится вставка?

Вставка в красно-черное дерево начинается со вставки элемента, как в обычном бинарном дереве поиска. Только здесь элементы вставляются в позиции NULL-листьев. Вставленный узел всегда окрашивается в красный цвет. Далее идет процедура проверки сохранения свойств красно-черного дерева .

Свойство 1 не нарушается, поскольку новому узлу сразу присваивается красный цвет.

Свойство 2 нарушается только в том случае, если у нас было пустое дерево и первый вставленный узел (он же корень) окрашен в красный цвет. Здесь достаточно просто перекрасить корень в черный цвет.

Свойство 3 также не нарушается, поскольку при добавлении узла он получает черные листовые NULL-узлы.

В основном встречаются 2 других нарушения:

1) Красный узел имеет красный дочерний узел (нарушено свойство ).

2) Пути в дереве содержат разное количество черных узлов (нарушено свойство ).

Подробнее о балансировке красно-черного дерева при разных случаях (их пять, если включить нарушение свойства ) можно почитать на wiki.

Это вообще где-то используется?

Да! Когда в институте на третьем курсе нам читали «Алгоритмы и структуры данных», я и не могла представить, что красно-черные деревья где-то используются. Помню, как мы не любили тему сбалансированных деревьев. Ох уж эти родственные связи в красно-черных деревьях («дядя», «дедушка», «чёрный брат и крестный красный отец»), прям Санта-Барбара какая-то. Правые и левые, малые и большие повороты АВЛ-деревьев – сплошные американские горки. Вы тоже не любите красно-черные деревья? Значит, просто не умеете их готовить. А кто-то просто взял и приготовил. Так, например, ассоциативные массивы в большинстве библиотек реализованы именно через красно-черные деревья.

Это все, что я хотела рассказать.

Источник