Чему равно хроматическое число дерева

Содержание

Хроматическое число планарного графа
Раскраска в 5 цветов
Раскраска в 4 цвета
Эквивалентные формулировки
Ложное доказательство
Источники информации
Раскрашивание графов
Хроматическое число

Хроматическое число планарного графа

Предположим, что для планарного графа с [math]N[/math] вершинами существует раскраска в [math]6[/math] цветов. Докажем то же для графа с [math] N+1 [/math] вершиной.

По только что доказанной лемме в [math] G [/math] найдётся вершина степени не больше [math]5[/math] . Удалим её; по предположению индукции получившийся граф можно раскрасить в [math]6[/math] цветов.

Раскраска в 5 цветов

Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Покажем что для случая с [math]5[/math] -ю цветами всё равно можно вернуть удалённую вершину так, чтобы раскраска осталась правильной.

Обозначим за [math] u [/math] — возвращаемую вершину, [math] v^ [/math] — вершину, покрашенную в [math] k [/math] цвет.

Если среди вершин, смежных [math] u [/math] , есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим [math] u [/math] .

Иначе, уложим полученный после удаления [math] u [/math] граф на плоскость, вернём вершину [math] u [/math] (пока бесцветную) и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке.

Попробуем покрасить [math] u [/math] в цвет [math]1[/math] . Чтобы раскраска осталась правильной, перекрасим смежную ей вершину [math]v_1^[/math] в цвет [math]3[/math] . Если среди смежных ей вершин есть вершины [math] v_i^ [/math] , покрасим их в цвет [math]1[/math] , и так далее. Рассмотрим две необычные ситуации, которые могут наступить во время обхода:

мы дойдём до уже однажды перекрашенной вершины (и хотим перекрасить её обратно, что не получится сделать). Видно что такая ситуация невозможна, поскольку мы меняли цвета вершин по схеме [math]1[/math] [math]\leftrightarrow[/math] [math]3[/math] , и если по завершении обхода мы получили две смежные вершины одного цвета, значит и до перекрасок в этом месте были две вершины одинакового цвета, а по предположению граф без [math] u [/math] был раскрашен правильно.
дойдём до вершины, смежной [math] u [/math] , исходно имевшей цвет [math]3[/math] , которую перекрасить в [math]1[/math] нельзя ( [math] u [/math] теперь имеет цвет [math]1[/math] ).

Если этот процесс был успешно завершён, то получили правильную раскраску. Если же в соответствии со вторым вариантом перекраска не удалась, это означает, что в графе есть цикл [math] u v_1^ v_2^ v_3^ \ldots v_^ v_k^ u [/math] .

Тогда попытаемся таким же образом перекрасить [math] u [/math] в цвет [math]2[/math] , а смежную ей [math]w_1^[/math] в цвет [math]4[/math] (со последующими перекрасками). Если удастся — раскраска получена.

Заметим, что не удаётся составить подобное доказательство для раскраски в четыре цвета, поскольку здесь наличие двух вершин одного цвета среди смежных [math] u [/math] не исключает того, что при их (смежных вершин) раскраске использовались все возможные цвета.

Раскраска в 4 цвета

Теорема о четырёх красках — утверждение о том, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются.

Теорема о четырёх красках была доказана в [math]1976[/math] году Кеннетом Аппелем и Вольфгангом Хакеном из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация того, что существует определенный набор из [math]1936[/math] карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Аппель и Хакен использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из [math]1936[/math] карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен бы содержать, хотя не содержит, какую-нибудь из этих [math]1936[/math] карт. Это противоречие говорит о том, что вообще не существует контрпримера. Изначально доказательство не было принято всеми математиками, поскольку его невозможно было проверить вручную. В дальнейшем оно получило более широкое признание, хотя у некоторых долгое время оставались сомнения.

Чтобы развеять оставшиеся сомнения, в [math]1997[/math] году Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера. Кроме того, в [math]2005[/math] году доказательство было проделано Джорджсом Гонтиром с использованием специализированного программного обеспечения (Coq v7.3.1)

Эквивалентные формулировки

В теории графов утверждение теоремы четырёх красок имеет следующие формулировки:

Хроматическое число планарного графа не превосходит [math]4[/math] .
Рёбра произвольной триангуляции сферы можно раскрасить в три краски так, что все стороны каждого треугольника были раскрашены в разные цвета.

Ложное доказательство

Ошибочным мнением считается, что решением проблемы четырех красок является — доказательство того, что невозможно начертить карту, на которой было бы всего лишь пять стран и каждая из этих стран примыкала бы к четырем остальным странам. Нетрудно доказать, что такую карту начертить нельзя. Можно предположить, что отсюда автоматически следует решение проблемы четырех красок для всех карт, но такое заключение неверно.

Карта(слева) окрашена пятью цветами, и нужно изменить как минимум [math]4[/math] из [math]10[/math] регионов, чтобы получить окраску в четыре цвета(справа)

Источники информации

Источник

Раскрашивание графов

Хроматическое число

Рассмотрим задачу: при каких условиях вершины графа можно раскрасить так, чтобы каждое ребро было инцидентно вершинам разного цвета? Нас больше всего интересует вопрос, какие графы можно раскрасить с соблюдением определенных условий, чем вопрос, сколькими способами можно выполнить это раскрашивание.

Пусть граф не имеет петель; тогда называется — раскрашиваемым , если каждой его вершине можно приписать один из цветов таким образом, чтобы никакие две смежные вершины не оказались одного цвета. Если граф является -раскрашиваемым, но не является (k-1) -раскрашиваемым, назовем его — хроматическим , а число назовем хроматическим числом графа и обозначим через $\chi (G)$ . На рисунке изображен 4-хроматический (и, следовательно, -раскрашиваемый граф при $k \ge 4$ ) граф ; цвета обозначены греческими буквами.

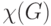
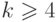
Для удобства будем предполагать, что все графы не содержат петель. Однако будем допускать существование кратных ребер, так как они не влияют на наши рассуждения.

$\chi(K_<n data-lazy-src=$

Ясно, что )=n»/>, и, следовательно, легко построить графы со сколь угодно большим хроматическим числом . С другой стороны, нетрудно видеть, что

тогда и только тогда, если — вполне несвязный граф , и что

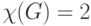
$\chi (G) =2$

тогда и только тогда, если — двудольный граф , отличный от вполне несвязного графа.

Теорема 8.1. Если наибольшая из степеней вершин графа равна $\rho$ , то этот граф $(\rho + 1)$ -раскрашиваем.

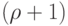
Доказательство Проведем индукцию по числу вершин в . Пусть — граф с вершинами; если из него удалить произвольную вершину вместе с инцидентными ей ребрами, то в оставшемся графе будет n-1 вершин, причем степени вершин по -прежнему не превосходят $\rho$ . По предположению индукции этот граф $(\rho+1)$ -раскрашиваем, отсюда получится $(\rho +1)$ -раскладка для , если окрасить вершину цветом, отличным от тех, которыми окрашены смежные с ней вершины, а их не более чем $\rho$ .

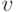
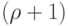
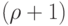
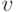
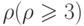
Теорема (Брукса). Пусть — простой связный граф , не являющийся полным; если наибольшая из степеней его вершин равна $\rho (\rho \ge 3)$ , то он $\rho$ -раскрашиваем.

Доказательство Проведем индукцию по числу вершин графа . Предположим, что имеет вершин. Если при этом степень какой-нибудь его вершины меньше $\rho$ , дальше можно рассуждать, как в доказательстве теоремы 1, и все будет закончено. Поэтому без потери общности можно считать граф регулярным степени $\rho$ .

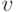
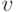
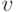
Выберем произвольную вершину и удалим ее, вместе с инцидентными ей ребрами. Останется граф с n-1 вершинами, в котором наибольшая из степеней вершин не превосходит $\rho$ . По предположению индукции этот граф $\rho$ -раскрашиваем. Теперь окрасим вершину в один из имеющихся $\rho$ цветов. Как и раньше, считаем, что смежные с вершины v_<1 data-lazy-src= \dts v_»/> расположены вокруг A_<1 data-lazy-src= ,c_ \dts c_»/>.

Определяя подграфы v_ лежат в разных компонентах графа i,j вершины ,v_»/> связаны простой цепью, целиком лежащей в H_<ij data-lazy-src= »/>, содержащую вершины C_<ij data-lazy-src= »/>.

Ясно, что если вершина c_<j data-lazy-src= »/>, то существует цвет, отличный от v_. Тогда вершину в цвет c_ и закончить на этом доказательство теоремы. Если этот случай не имеет места, то используем аналогичное рассуждение, чтобы показать, что каждая вершина из v_ и от — первая вершина простой цепи из »/> в можно перекрасить в цвет, отличный от c_ или »/> и C_<ij data-lazy-src= »/>. Поэтому мы можем считать, что для любых компонента »/> состоит только из простой цепи, соединяющей вершину v_<j data-lazy-src= »/>.

Заметим теперь, что две простые цепи вида C_<jl data-lazy-src= »/>, где , так как если — другая точка пересечения, то ее можно перекрасить в цвет, отличный от c_ или c_<l data-lazy-src= »/>, а это противоречит факту, что v_ и допустим, что , смежная с »/>. Поскольку $l\ne j$ ), можно поменять между собой цвета вершин в этой цепи, не затрагивая раскраску остальной части графа. Но это приводит к противоречию, потому что тогда будет общей вершиной простых цепей C_<ij data-lazy-src= »/> и v_ и должен быть полным графом $K_<\rho +1 data-lazy-src=$ »/>. А так как это не допускается условием теоремы, то все возможные случаи рассмотрены.

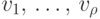
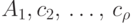
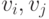
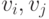
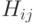
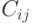
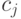
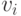
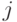
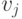
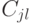
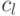
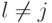
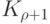Источник