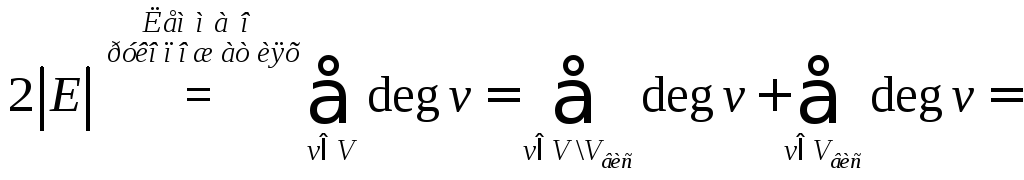§9. Метрические характеристики графа
Пусть G = (S, U) – связный граф и xi, xj – две его произвольные вершины.
Определение 9.1. Расстоянием d(xi, xj) между вершинами xi и xj называется длина кратчайшего маршрута, соединяющего эти вершины.
Из определения 9.1 непосредственно следует:
Определение 9.2. Эксцентриситетом вершины x называется величина
e(x) = (9.1)
Таким образом, эксцентриситет вершины равен расстоянию от данной вершины до наиболее удалëнной от неë.
Определение 9.3. Диаметром d(G) графа G называется максимальный из всех эксцентриситетов вершин графа G, т.е.
Определение 9.4. Вершина x называется периферийной, если e(x) = d(G).
Определение 9.5. Диаметральной цепью называется простая цепь, расстояние между концами которой равно d(G).
Теорема 9.1. Для любого связного графа G справедливо неравенство
d(G) rank G.
Определение 9.6. Радиусом r(G) графа G называется минимальный из всех эксцентриситетов вершин графа G, т.е.
Определение 9.7. Вершина x называется центральной, если e(x) = r(G).
Определение 9.8. Множество всех центральных вершин графа называется его центром.
Заметим, что центр может состоять как из одной, так и из нескольких вершин.
Пример 9.1. Найти эксцентриситеты вершин, радиусы и диаметры графа G, изображëнного на рис. 16, периферийные и центральные вершины. Привести
пример диаметральной цепи.
Р ешение. Найдëм эксцентриситеты всех вершин G: e(x1) = e(x4) = e(x5) = 4,
e(x2) = e(x6) = e(x7) = e(x8) = 3, e(x3) = 2.
Следовательно, d(G) = 4, r(G) = 2. Получаем, что вершины x1, x4 и x5 являются периферийными, а вершина x3 – центральной. Одной из диаметральных цепей является
x1 – x7 – x3 – x6 – x5.
§10. Деревья и их свойства. Лес
Определение 10.1. Любой связный неорграф, не содержащий циклов, называется (неориентированным) деревом.
Определение 10.2. Любой неорграф без циклов называется лесом, или ациклическим графом.
Таким образом, компонентами связности любого леса являются деревья.
На рис. 17 показан лес, состоящий из двух деревьев.
Свойства деревьев сформулируем в виде следующей теоремы.
Теорема 10.1. Пусть G = (S, U) и = n, = m. Тогда следующие условия эквивалентны:
- G – дерево;
- G – связный граф и m=n1;
- G – ациклический граф и m=n1;
- любые две различные вершины графа соединяет единственная простая цепь;
- G – ациклический граф, такой, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
Теорема 10.2 (Кэли). Число деревьев с n занумерованными вершинами равно .
Определение 10.3. Ориентированным деревом (ордеревом) называется
орграф G = (S, U), удовлетворяющий следующим двум условиям:
- существует единственная вершина xiS, называемая корнем, не имеющая предшествующих вершин (т. е. );
- любой вершине xj, отличной от xi, в орграфе G непосредственно предшествует ровно одна вершина (т. е. ).
Определение 10.4. Узлом ордерева называется вершина, отличная от корня.
Определение 10.5. Листом ордерева называется вершина x такая, что и
Определение 10.6. Ветвью ордерева называется путь из корня в лист.
Определение 10.7. Высотой ордерева называется длина его наибольшей ветви.
Определение 10.8. Уровнем вершины ордерева называется расстояние от корня до этой вершины.
Отметим, что корень имеет уровень 0.
Определение 10.9. Ярусом ордерева называется множество вершин одного уровня.
Замечание 10.1. Неориентированное дерево можно преобразовать в ориентированное, выбрав в качестве корня произвольную вершину. На рис. 18 корень графа – вершина x7.
П ример 10.1. Рассмотрим ордерево, изображëнное на рис. 18. Тогда: все вершины, кроме x7, являются узлами ордерева; вершины x1, x5, x8, x10, x11, x12 – листами; путь x7 x6 x3 x2 x10 – одна из ветвей; высота ордерева равна 5; множество вершин x1, x5, x9, x10> уровня 4 образует один из ярусов ордерева.
Определение 10.10. Остовом неорграфа G = (S, U) называется его часть G = (S, U), такая, что S = S и G – лес, образующий дерево на любой связной компоненте графа G.
Из определения 10.10 следует, что если G – связный неорграф, то остов G является деревом, которое будем называть остовным деревом графа G.
Определение 10.11. Остовом орграфа G называется его часть G, такая, что ассоциированный с G неорграф F(G) является остовом графа F(G).
Понятие остовного дерева для связного орграфа вводится аналогично.
Замечание 10.2. 1) В каждом графе существует остов, который можно получить, разрушая в каждой связной компоненте циклы, т.е. удаляя лишние рëбра.
2) Остов графа определяется неоднозначно.
П ример 10.2. На рис. 19 изображены неорграф G и один из его остовов G.
Для подсчета числа остовов в неорграфе используется матрица Кирхгофа.
Теорема 10.3 (Кирхгофа). Число остовных деревьев в связном неорграфе G порядка n 2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
Из определения дерева вытекает следующая теорема.
Теорема 10.4. Пусть G = (S, U) – произвольный неорграф, = n, = m , k – число компонент связности графа G. Число рëбер, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m – n + k.
Доказательство. Пусть i-я компонента связности Gi содержит ni вершин и mi рëбер. По условию G – связный граф. Следовательно, остов Gi графа Gi является деревом, а значит, он содержит (ni – 1) ребро. Таким образом, для получения остова Gi из i-й компоненты связности Gi требуется удалить mi – (ni – 1) ребер.
Просуммируем удаляемые ребра по всем компонентам связности, учитывая, что Получим
Определение 10.12. Число (G) = m n + k называется цикломатическим числом или циклическим рангом графа G.
Определение 10.13. Число *(G) = n k называется коциклическим рангом или корангом.
Таким образом, *(G) равно числу рëбер, входящих в любой остов графа G. Очевидно, что (G) +*(G) = m.
Из теоремы 10.4 непосредственно вытекают два следствия.
Следствие 10.4.1. Неорграф G является лесом тогда и только тогда, когда
Следствие 10.4.2. Неорграф G имеет единственный цикл тогда и только тогда, когда (G) =1.
Пример 10.3. Найти для графа G, изображенного на рис. 19, цикломатическое число и коциклический ранг.
Решение. Граф G имеет 8 вершин, 14 ребер и 1 компоненту связности. Тогда, согласно по теореме 10.4, цикломатическое число (G) = 14 – 8 +1 = 7, а коциклический ранг *(G) = 8 – 1 = 7 .
Источник
Поиск компонент связности
Компонентой связности неориентированного графа называется подмножество вершин, достижимых из какой-то заданной вершины. Как следствие неориентированности, все вершины компоненты связности достижимы друг из друга.
Дан неориентированный граф $G$ с $n$ вершинами и $m$ рёбрами. Требуется найти в нём все компоненты связности, то есть разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами путей не существует.
Для решения задачи модифицируем обход в глубину так, чтобы запустившись от вершины какой-то компоненты, от пометил все вершины этой компоненты — то есть все достижимые вершины — заданным номером этой компоненты. Для этого можно массив used заменить массивом номеров компонент для каждой вершины, изначально заполненный нулями:
Теперь проведем серию обходов: сначала запустим обход из первой вершины, и все вершины, которые он при этом обошёл, образуют первую компоненту связности. Затем найдём первую из оставшихся вершин, которые ещё не были посещены, и запустим обход из неё, найдя тем самым вторую компоненту связности. И так далее, пока все вершины не станут помеченными.
Записывается это очень компактно:
После этого переменная num будет хранить число компонент связности, а массив component — номер компоненты для каждой вершины, который, например, можно использовать, чтобы быстро проверять, существует ли путь между заданной парой вершин.
Итоговая асимптотика составит $O(n + m)$, потому что такой алгоритм не будет запускаться от одной и той же вершины дважды, и каждое ребро будет просмотрено ровно два раза (с одного конца и с другого).
Источник
3.9. Деревья и леса
Каждая компонента связности леса – дерево, следовательно, для 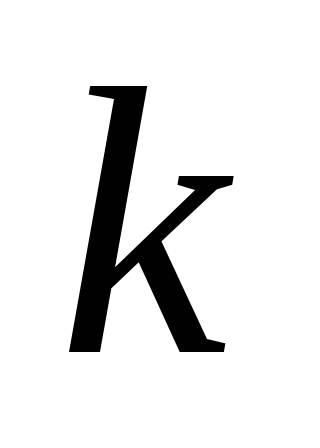

П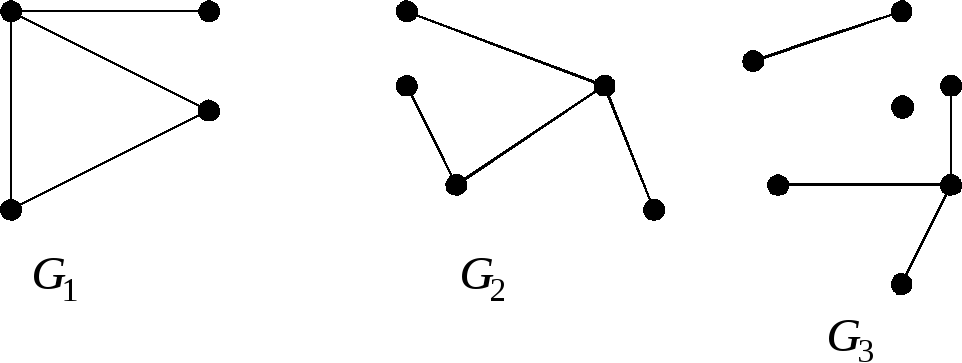


Лемма. Если граф – дерево, то каждое его ребро является мостом.
Доказательство.В параграфе 3.6 было доказано, что если ребро графа не содержится ни в одном цикле, то оно является мостом. Дерево граф ациклический, следовательно, каждое его ребро мост.■
Теорема (основная теорема о деревьях). Для графа следующие утверждения равносильны:
- Граф
— дерево.
ациклический и
.
связный и
.
связный и каждое его ребро является мостом.
- Любые две вершины графа
можно соединить, притом единственной, простой цепью.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
Доказательство.Доказательство проведем по следующей схеме:


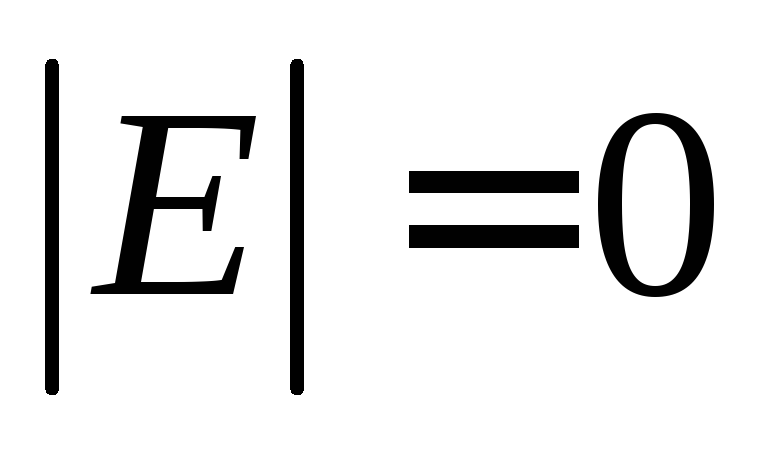
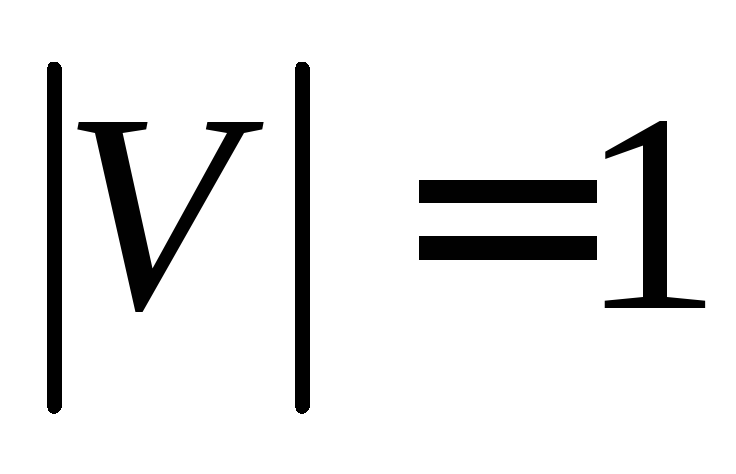
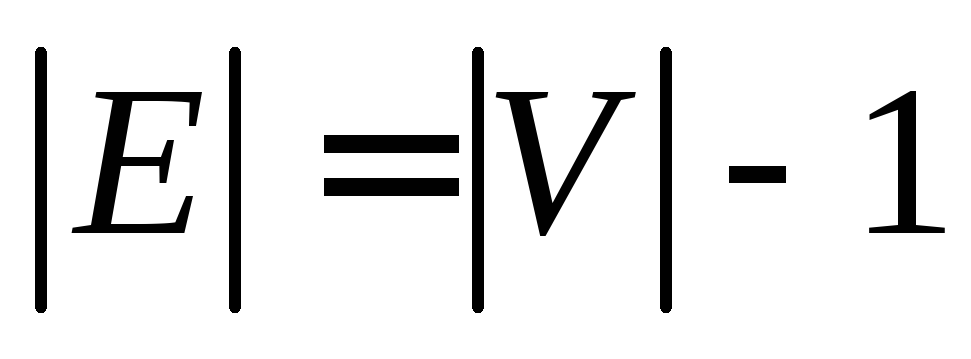




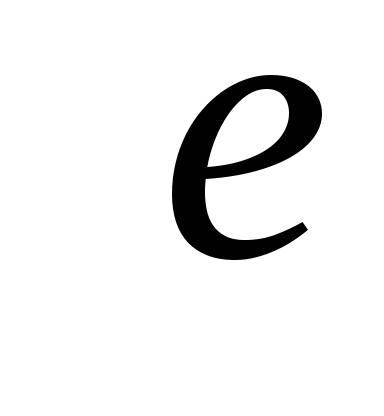
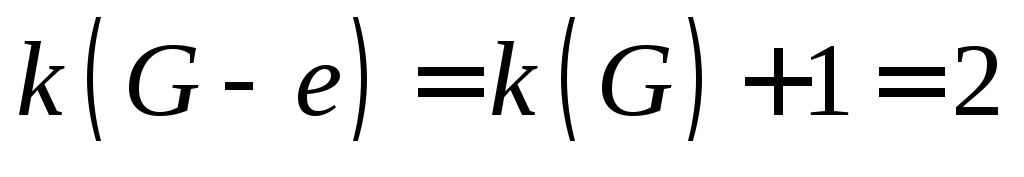
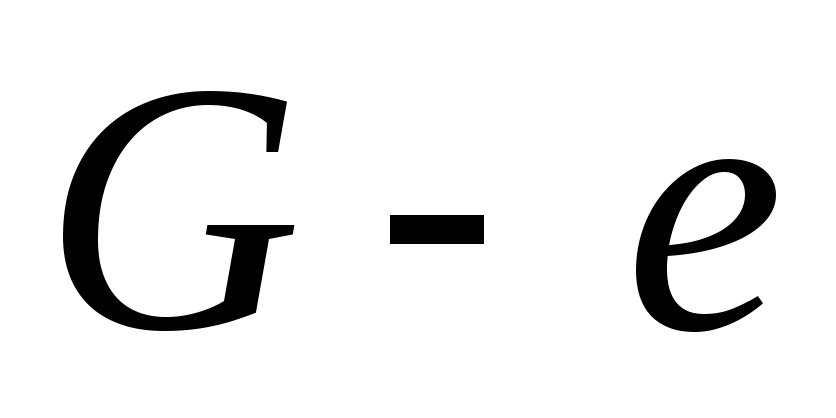
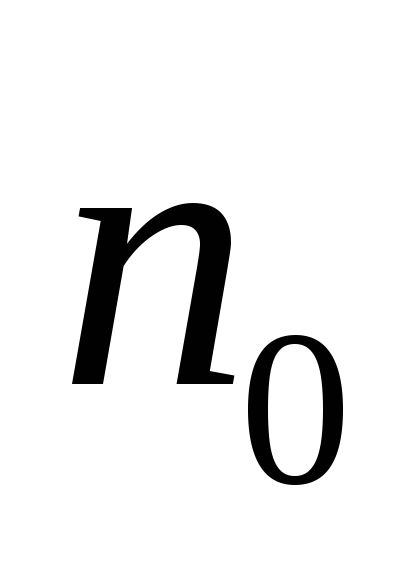
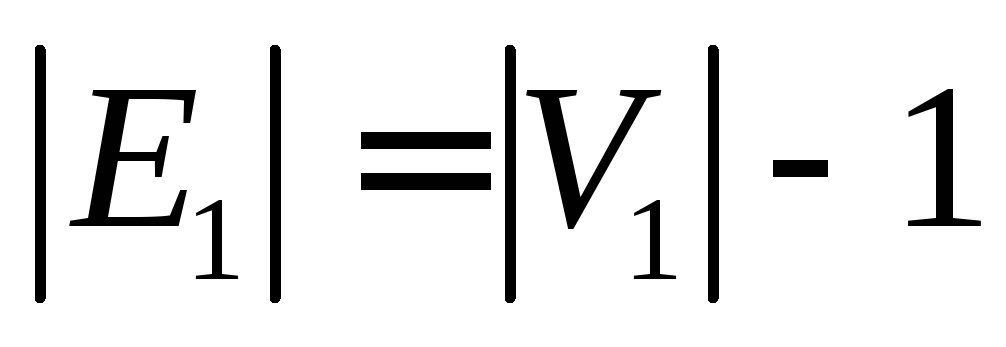
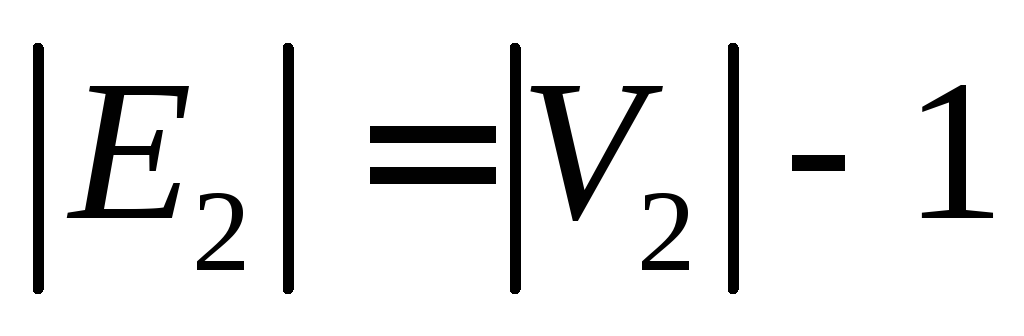



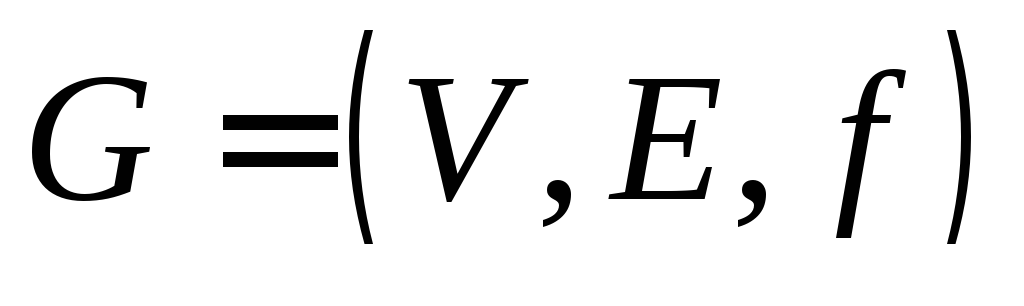
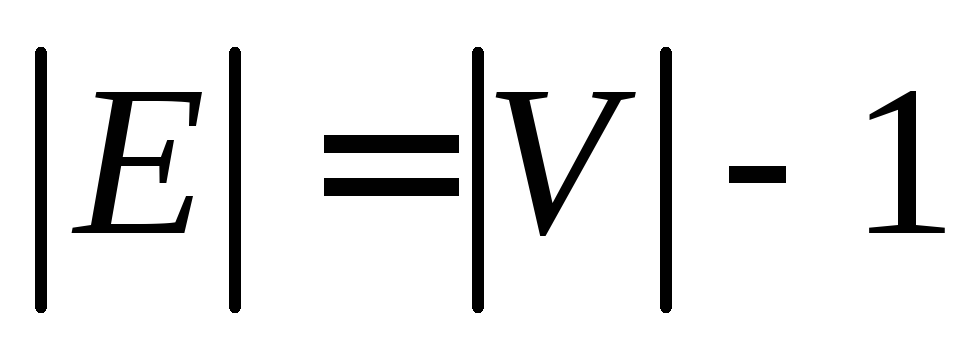

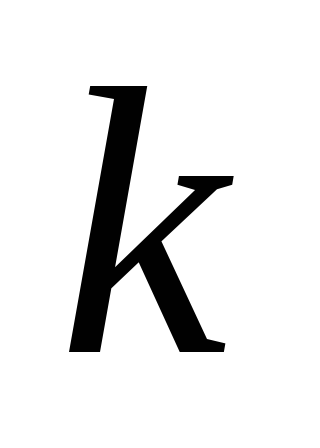











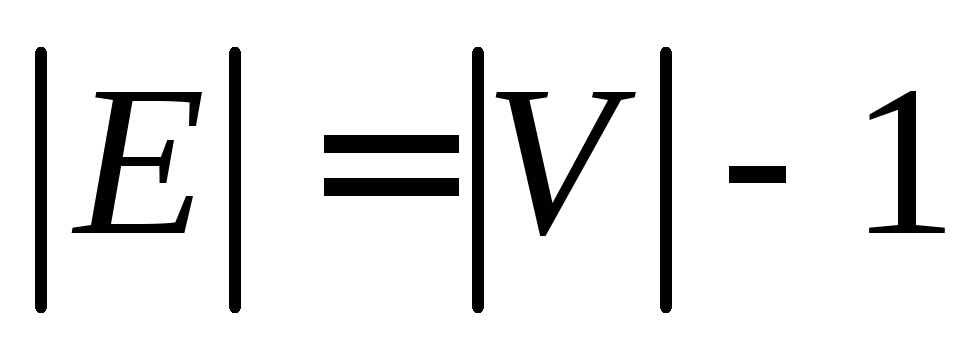



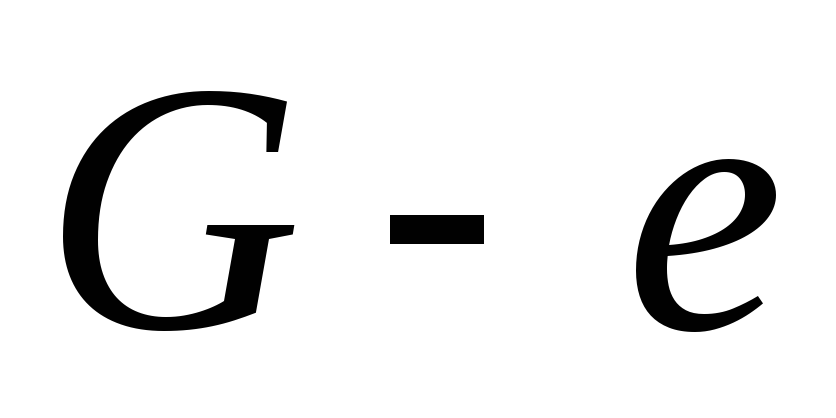
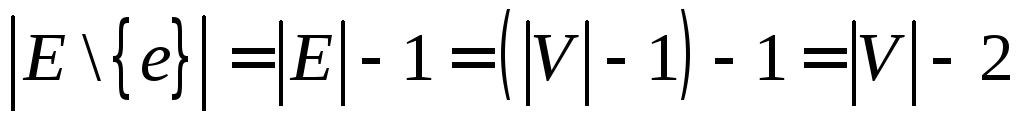
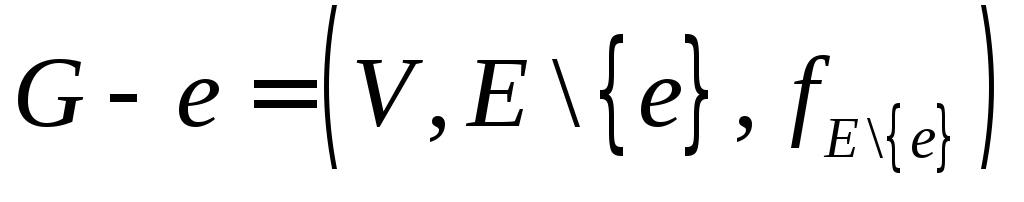











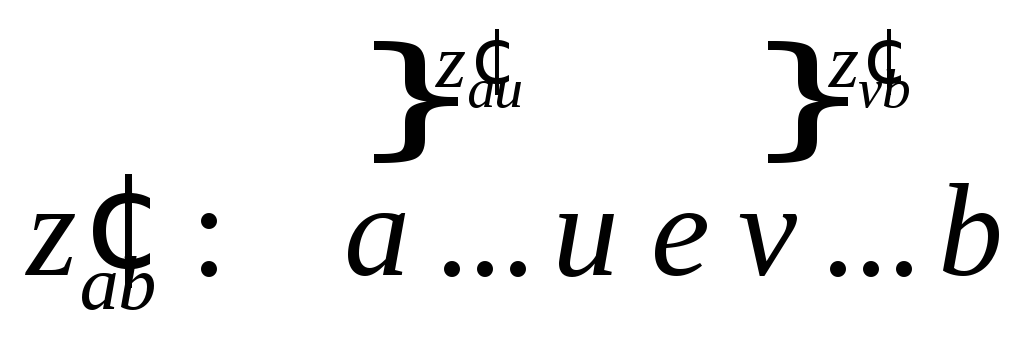





































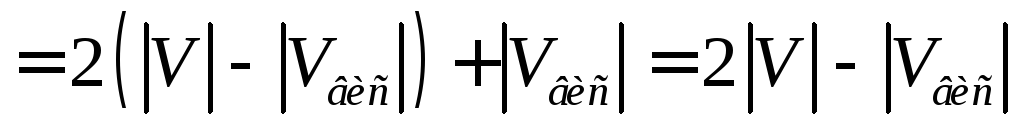





Источник


 — дерево.
— дерево. ациклический и
ациклический и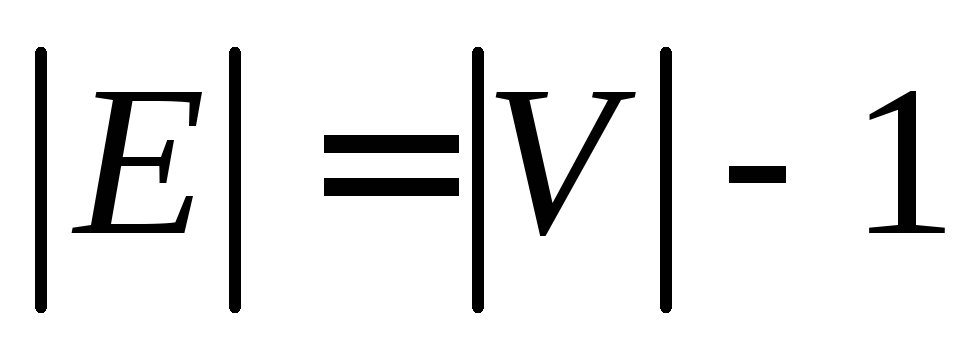 .
. связный и
связный и .
. связный и каждое его ребро является мостом.
связный и каждое его ребро является мостом. можно соединить, притом единственной, простой цепью.
можно соединить, притом единственной, простой цепью. ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.