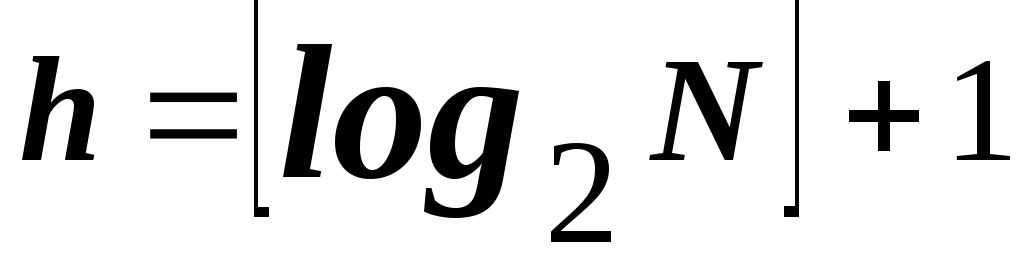Бинарные деревья
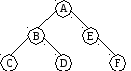
Хотя деревья общего вида достаточно важны, мы сосредоточимся на ограниченном классе деревьев, где каждый родитель имеет не более двух сыновей (рис. 4). Такие бинарные деревья (binary trees) имеют унифицированную структуру, допускающую разнообразные алгоритмы прохождения и эффективный доступ к элементам. Изучение бинарных деревьев дает возможность решать наиболее общие задачи, связанные с деревьями, поскольку любое дерево общего вида можно представить эквивалентным ему бинарным деревом.
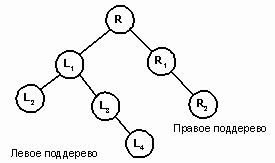
У каждого узла бинарного дерева может быть 0, 1 или 2 сына. По отношению к узлу слева будем употреблять термин левый сын (left child), а по отношению к узлу справа – правый сын (right child). Наименования «левый» и «правый» относятся к графическому представлению дерева. Бинарное дерево является рекурсивной структурой. Каждый узел – это корень своего собственного поддерева. У него есть сыновья, которые сами являются корнями деревьев, называемых левым и правым поддеревьями соответственно. Таким образом, процедуры обработки деревьев рекурсивны.
Дадим рекурсивное определение бинарного дерева.
Бинарное дерево — это такое множество узлов B, что
а) B является деревом, если множество узлов пусто (пустое дерево – тоже дерево);
б) B разбивается на три непересекающихся подмножества:
Рис.4. Пример бинарного дерева
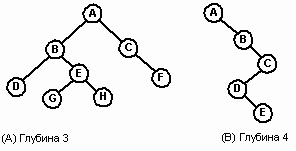
На любом уровне n бинарное дерево может содержать от 1 до 2n узлов. Число узлов, приходящееся на уровень, является показателем плотности дерева. Интуитивно плотность есть мера величины дерева (число узлов) по отношению к глубине дерева. На рис. 4 дерево А содержит 8 узлов при глубине 3, в то время как дерево B содержит 5 узлов при глубине 4. Последний случай является особой формой, называемой вырожденным (degenerate) деревом, у которого есть единственный лист (E) и каждый нелистовой узел имеет только одного сына. Вырожденное дерево эквивалентно связанному списку.
Рис.5. Бинарные деревья различной плотности
Деревья с большой плотностью очень важны в качестве структур данных, так как позволяют хранить большие коллекции данных и осуществлять эффективный доступ к элементам. Быстрый поиск – главное, что обусловливает использование деревьев для хранения данных.
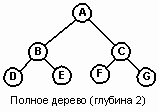
Вырожденные деревья имеют наименьшую плотность (1). Другая крайность – законченные бинарные деревья (complete binary tree) глубины N, где каждый уровень 0, 1, . N-1 имеет полный набор узлов, и все листья уровня N расположены слева. Законченное бинарное дерево, содержащее 2N узлов на уровне N, является полным. На Рис. 6 показаны законченное и полное бинарные деревья.
Законченные и полные бинарные деревья дают интересные математические факты. На нулевом уровне имеется 2 0 узлов, на первом — 2 1 , на втором — 2 2 и т.д. На первых k-1 уровнях имеется 2 k-1 узлов.
1 + 2 + 4 + . + 2 k-1 = 2 k -1
На уровне k количество дополнительных узлов колеблется от 1 до 2k (полное). В полном дереве число узлов равно
1 + 2 + 4 + . + 2 k-1 + 2 k = 2 k-1 — 1
Число узлов законченного бинарного дерева удовлетворяет неравенству
2 k N 2 k-1 — 1 2 k-1
Решая его относительно k, имеем
k log2 (N) k+1
Например, полное дерево глубины 3 имеет
2 4 — 1 = 15 узлов
Рис.6. Классификация бинарных деревьев
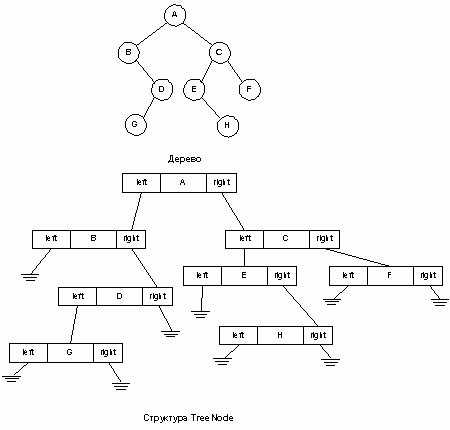
Структура бинарного дерева
Структура бинарного дерева состоит из узлов (рис.7). Как и в связанном списке, эти узлы содержат поля данных и указатели на другие узлы в коллекции. В этом разделе мы определим узлы дерева и операции для его построения и прохождения. Объявим класс TreeNode, реализующий функциональность узла дерева, и разработаем ряд функций, позволяющих создавать бинарные деревья и осуществлять прохождение по их узлам.
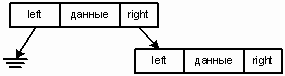
Узел дерева содержит поле данных и два поля с указателями. Поля указателей называются левым указателем (left) и правым указателем (right), поскольку они указывают на левое и правое поддерево, соответственно. Значение NULL является признаком пустого дерева.
Рис.7. Структура узлов дерева
Корневой узел определяет входную точку дерева, а поля указателей – узлы следующего уровня. Листовой узел содержит NULL в полях правого и левого указателей. Пример представления структуры дерева дан на рис. 8.
Рис.8. Представление структуры дерева
Источник
7.2. Бинарные деревья
Особенно важное практическое значение имеют упорядоченные деревья второй степени. Их называют двоичными или бинарными деревьями.
Бинарное дерево– это конечное множество узлов, которое или пусто, или состоит из корня и двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями данного корня. Примеры бинарных деревьев приведены на рис. 65.
Рис. 65. Примеры бинарных деревьев
Максимальное число узлов в бинарном дереве высотой h (d=2):
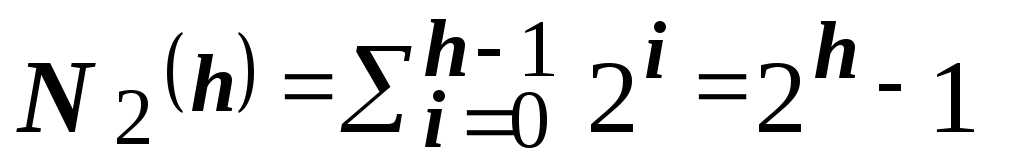
Максимальное число узлов на уровне i в бинарном дереве:
.
Высота полного бинарного дерева, содержащего Nузлов:
.
означает взятие целой части числа.
Существуют различные алгоритмы преобразования дерева произвольной степени, т.е. дерева общего вида, к виду бинарного. Левосторонний алгоритм формулируется следующим образом: у каждого узла дерева произвольной степени необходимо сохранить самую левую связь, а узлы – потомки одного и того же узла следует соединить правой связью. На рис. 66 представлено исходное дерево общего вида, а на рис. – эквивалентное бинарное.
Рис. 66. Преобразование произвольного дерева к виду бинарного
7.3. Представление бинарных деревьев
7.3.1. Представление бинарных деревьев на статической
Если известен максимальный размер дерева (т.е. высота, а следовательно, и количество узлов, соответствующих полному дереву), то структуру дерева можно хранить в виде массива. При этом корень дерева будет храниться в элементе массива с индексом [1]. Для каждого узла с номеромkего левый потомок будет хранится в элементе с индексом[2 * k], а правый — в элементе с индексом[2 * k + 1] (см. рис. 67).
Рис. 67. Представление бинарного дерева на статической памяти
Достоинством представления бинарных деревьев на статической памяти является простота доступа как от предка к потомку, так и от потомка к предку, а недостатком — то, что если дерево не является полным, в массиве появляется большое число пустых элементов. Ограниченный размер массива не позволяет включать в дерево новые узлы, т.е. дерево не может “расти”. Удаление узла из дерева и соответствующее изменение его структуры потребует модификации содержимого массива.
7.3.2. Представление бинарных деревьев на
Элемент хранения узла бинарного дерева состоит из одного или нескольких информационных полей и двух полей связи, указывающих соответственно на левое и правое поддеревья данного узла.
Источник