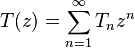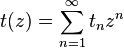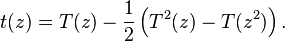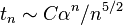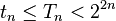Дерево (теория графов) кратко
Привет, сегодня поговорим про дерево в теории графов , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дерево в теории графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.. Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути. Лес — упорядоченное множество упорядоченных деревьев. Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в нее не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведет ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями. Корневое дерево — дерево, в котором выделена одна вершина (корень дерева). Формально корневое дерево определяется как конечное множество 
- существует один корень дерева
- остальные узлы (за исключением корня) распределены среди
непересекающихся множеств
, и каждое из множеств является корневым деревом; деревья
называются поддеревьями данного корня
Связанные определения
- Степень узла — количество исходящих дуг (или, иначе, количество поддеревьев узла).
- Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведет только одно ребро; в случае ориентированного дерева — узел, в который ведет только одна дуга и не исходит ни одной дуги).
- Узел ветвления — неконцевой узел.
- Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:
- уровень корня дерева
равен 0;
- уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева
, содержащего данный узел.
- Дерево с отмеченной вершиной называется корневым деревом.
-й ярус дерева
— множество узлов дерева, на уровне
от корня дерева.
- частичный порядок на вершинах:
, если вершины
и
различны и вершина
лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной
.
- корневое поддерево с корнем
— подграф
.
- В контексте, где дерево предполагается имеющим корень, дерево без выделенного корня называется свободным.
- Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом . Об этом говорит сайт https://intellect.icu . Ребра графа, не входящие в остов, называютсяхордами графа относительно остова.
- Несводимым называется дерево, в котором нет вершин степени 2.
- Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
Двоичное дерево
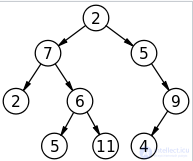
Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.
Термин двоичное дерево (оно же бинарное дерево) имеет несколько значений:
- Неориентированное дерево, в котором степени вершин не превосходят 3.
- Ориентированное дерево, в котором исходящие степени вершин (число исходящих ребер) не превосходят 2.
- Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, какдвоичное дерево поиска, двоичная куча, красно-черное дерево, АВЛ-дерево, фибоначчиева куча и др.
N-арные деревья
N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.
- N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
- N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих ребер) не превосходят N.
Свойства
- Дерево не имеет кратных ребер и петель.
- Любое дерево с
вершинами содержит
ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда
, где
— число вершин,
— число ребер графа.
- Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственной простой цепью.
- Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.
- Любое дерево является двудольным графом. Любое дерево, множество вершин которого не более чем счетное, является планарным графом.
- Для любых трех вершин дерева, пути между парами этих вершин имеют ровно одну общую вершину.
Подсчет деревьев
- Число различных деревьев, которые можно построить на
нумерованных вершинах, равно
(Теорема Кэли о числе деревьев ).
- Производящая функция
для числа 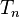
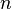
.
для числа 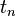
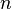
- При верна следующая асимптотика
где 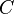
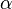
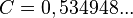
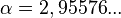
Кодирование деревьев
Дерево можно кодировать наборами из нулей и единиц. Рассмотрим, например, укладку дерева на плоскости. Начиная с какой либо вершины, будем двигаться по ребрам дерева, сворачивая в каждой вершине на ближайшее справа ребро и поворачивая назад в концевых вершинах дерева. Проходя по некоторому ребру, записываем 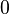
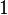
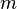
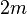
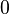
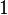
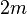
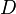
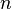
Вау!! 😲 Ты еще не читал? Это зря!
- Гипердерево
- Древовидная структура
- Дерево (структура данных)
- Древо решений
- Псевдолес
- Некорневое двоичное дерево
Я хотел бы услышать твое мнение про дерево в теории графов Надеюсь, что теперь ты понял что такое дерево в теории графов и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Источник
Что такое дерево графы
Поиск значения в BST занимает O(log n) времени. Это означает, что можно очень быстро найти требуемое значение среди миллионов или даже миллиардов записей.
Предположим, мы ищем узел со значением x. Чтобы быстро найти его в BST, воспользуемся следующим алгоритмом:
- Начать с корня дерева.
- Если x = значению узла: остановиться.
- Если x < значения узла: перейти к левому дочернему узлу.
- Если x > значения узла: перейти к правому дочернему узлу.
- Перейти к шагу 2.
При отсутствии уверенности в существовании искомого узла, необходимо изменить шаги 3 и 4 для остановки поиска.
Если хочешь подтянуть свои знания по алгоритмам, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в теорию структур данных;
- научишься решать сложные алгоритмические задачи;
- научишься применять алгоритмы и структуры данных при разработке программ.
Реализация
Создание узла TreeNode идентично созданию узла ListNode . Единственное отличие в том, что вместо одного атрибута у нас два: left и right , которые ссылаются на левые и правые дочерние узлы.
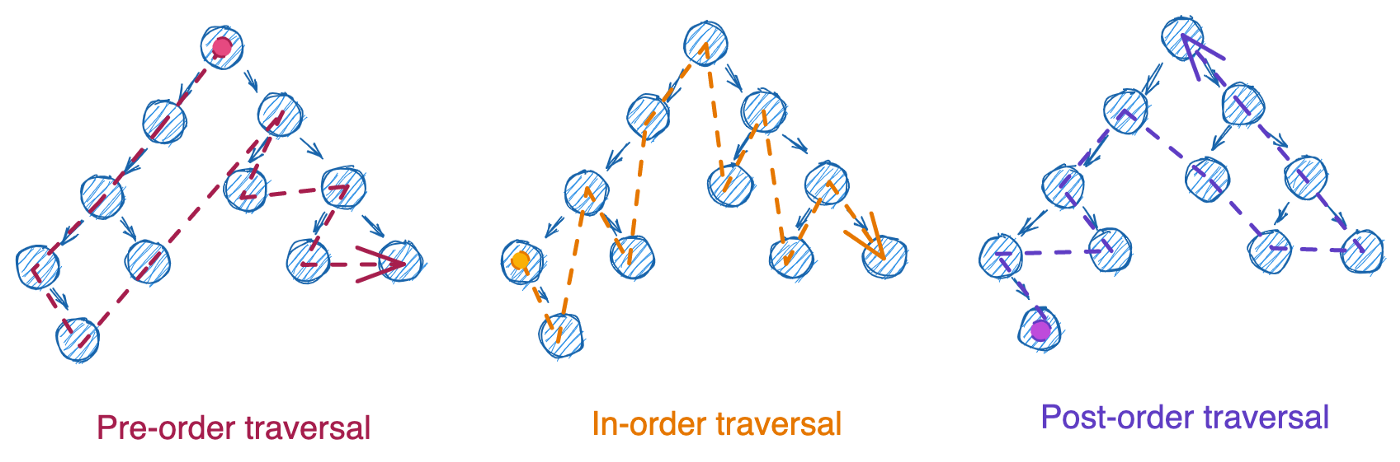
Эти три типа обхода могут быть реализованы следующими методами:
- с итерацией – использование цикла while и стека. В этом случае удаление данных возможно только с конца.
- с рекурсией – использование функции, которая вызывает сама себя.
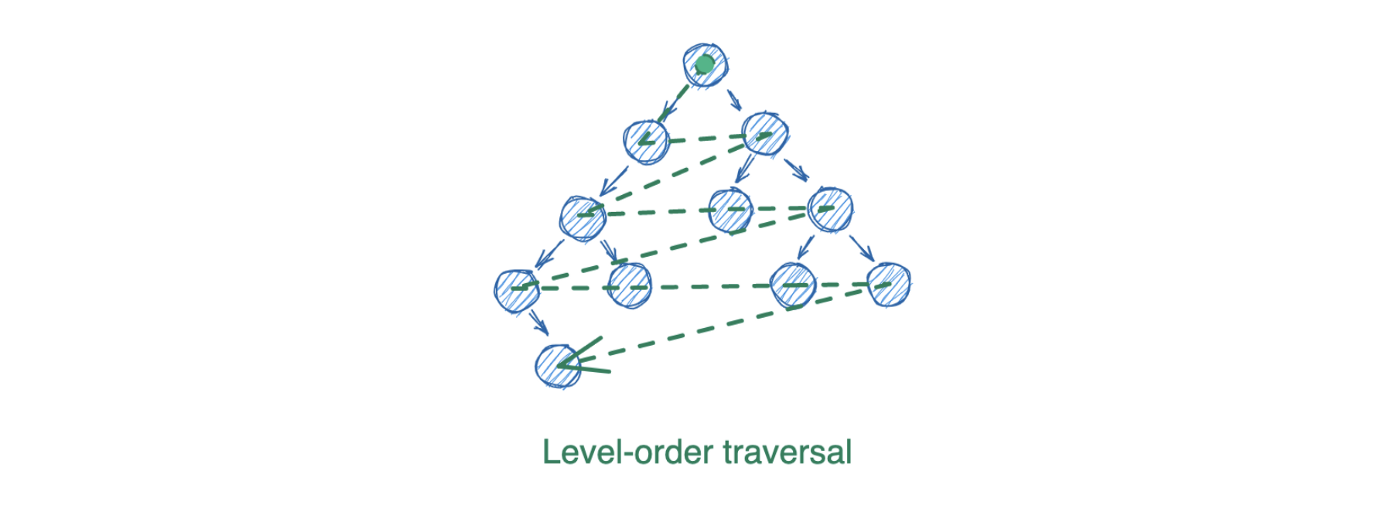
Есть четвертый тип обхода – порядок уровней (level-order traversal). Этот способ использует очередь (queue). Удаление данных здесь возможно только с начала.
Для первых трех типов обработки узлов паттерны практически идентичны. Просто выберем обход в порядке возрастания. Ниже разберем итеративный и рекурсивный методы для LC 94: Binary Tree Inorder Traversal, начиная с итеративной версии:
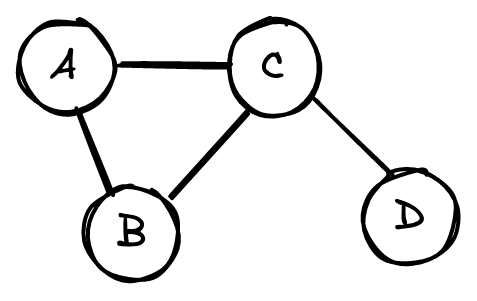
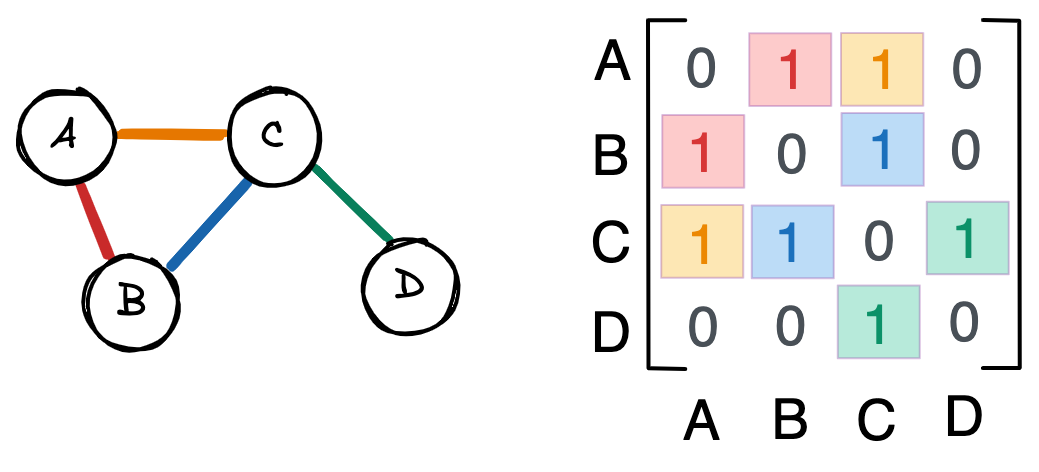
Как правило, графы представлены в виде матриц смежности (adjacency matrix). Так, у приведенного выше графа будет следующая матрица.
Каждая строка и столбец представляют собой узел. Единица в строке i и столбце j , или A_=1 , означает связь между узлом i и узлом j .
A_=0 означает, что узлы i и j не связаны.
Ни один из узлов в этом графе не связан с самим собой. Следовательно, диагональ матрицы равна нулю. Аналогично, A_ = A_ , потому что связи ненаправленны. То есть если узел A связан с узлом B , то B связан с A . В результате матрица смежности симметрична по диагонали.
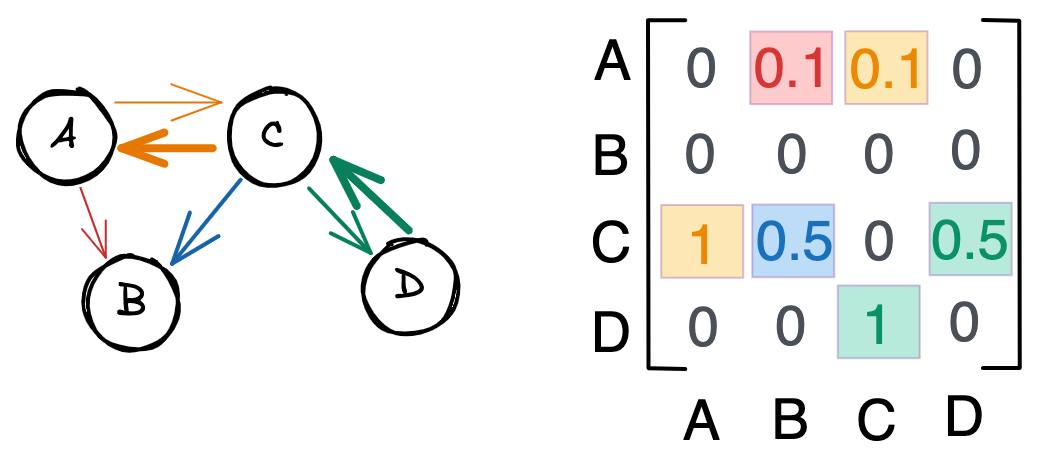
Рассмотрим пример, который поможет нам понять описанную выше теорию.
На представленных рисунках мы видим взвешенный граф с направленными ребрами. Обратите внимание, что связи больше не симметричны – вторая строка матрицы смежности пуста, потому что у B нет исходящих связей. Числа от 0 до 1 отражают силу связи. Например, граф C влияет на граф A сильнее, чем A на C .
Реализация
Реализуем невзвешенный и неориентированный граф. Основной структурой класса является список списков Python. Каждый из них – это строка. Индексы в списке представляют собой столбцы. При создании объекта Graph необходимо указать количество узлов n, чтобы создать список списков. Затем мы можем получить доступ к соединению между узлами a и b с помощью self.graph[a][b] .
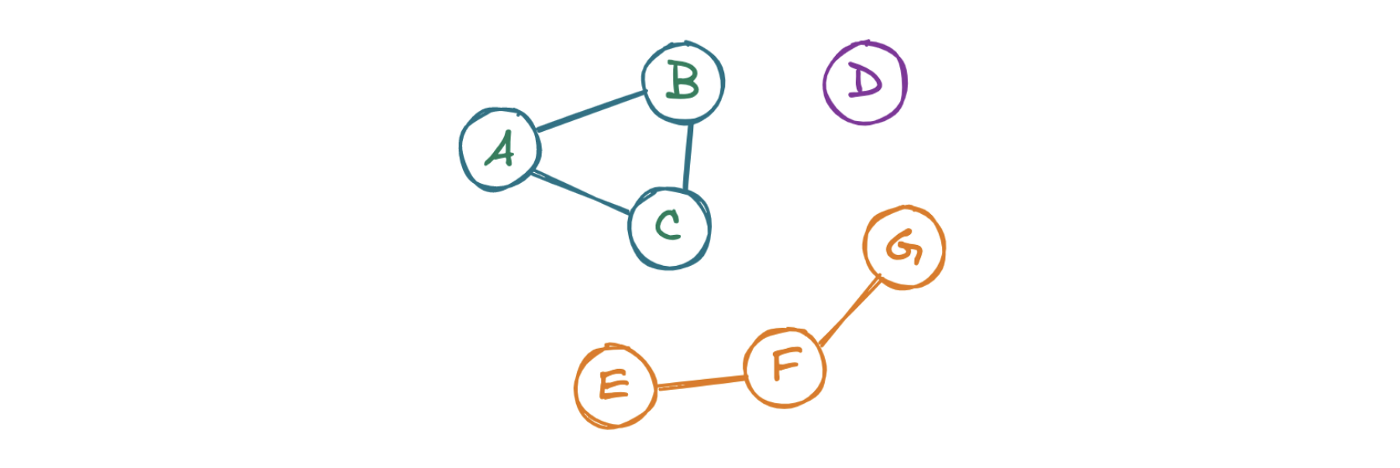
Чтобы ответить на вопрос LC 323: Количество связных компонентов, изучим каждый узел графа. Далее «посетим» соседние графы. Повторяем операцию до тех пор, пока не встретим только те узлы, которые уже были замечены программой. После этого проверим наличие в графе узлов, которые еще не были замечены. Если такие узлы присутствуют, то существует еще как минимум один кластер, поэтому нужно взять новый узел и повторить процесс.
def get_n_components(self, mat: List[List[int]]) -> int: """ Учитывая матрицу смежности, возвращает количество связанных компонентов """ q = [] unseen = [*range(len(mat))] answer = 0 while q or unseen: # Если все соседние узлы прошли через цикл, переходим к новому кластеру if not q: q.append(unseen.pop(0)) answer += 1 # Выбираем узел из текущего кластера focal = q.pop(0) i = 0 # Поиск связей во всех оставшихся узлах while i < len(unseen): node = unseen[i] # Если узел подключен к центру, добавляем его в очередь # чтобы перебрать его соседей # из невидимых узлов и избежать бесконечного цикла if mat[focal][node] == 1: q.append(node) unseen.remove(node) else: i += 1 return answer- Строки 5-8: Создаем очередь ( q ), список узлов ( unseen ) и количество компонентов ( answer ).
- Строка 10: Запускаем цикл while , который выполняем до тех пор, пока в очереди есть узлы, которые нужно обработать или узлы, которые не были замечены.
- Строки 13-15: Если очередь пуста, удаляем первый узел из непросмотренных и увеличиваем количество компонентов.
- Строки 18-19: Выбираем следующий доступный узел в очереди ( focal ).
- Строка 22: Запускаем цикл while , который выполняем до тех пор, пока не обработаем все оставшиеся узлы.
- Строка 23: Даем имя текущему узлу для оптимизации кода.
- Строки 28-30: Если текущий узел подключен к центру, добавляем его в очередь узлов текущего кластера. Удаляем его из списка тех узлов, которые могут находиться в невидимом кластере. Благодаря этому действию, мы избегаем бесконечного цикла.
- Строки 31-32: Если текущий узел не подключен к focal (центру), переходим к следующему узлу.
Заключение
Графы и деревья – основные структуры данных. Спектр их применения огромен. Например, графы используются там, где необходим алгоритм поиска решений. Реальный пример их использования – sea-of-nodes JIT-компилятора.
Деревья используются тогда, когда мы должны произвести быстрое добавление/удаление объекта с поиском по ключу. Например, в различных словарях и индексах БД (Баз данных). Кроме того, деревья являются неотъемлемой частью случайного леса – алгоритма машинного обучения.
В следующей части материала мы приступим к изучению хэш-таблиц.
Базовый и продвинутый курс «Алгоритмы и структуры данных» включает в себя:
- Живые вебинары 2 раза в неделю.
- 47 видеолекций и 150 практических заданий.
- Консультации с преподавателями курса.
Материалы по теме
Источник
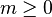 непересекающихся множеств
непересекающихся множеств 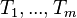 , и каждое из множеств является корневым деревом; деревья
, и каждое из множеств является корневым деревом; деревья 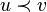 , если вершины
, если вершины 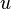 и
и 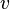 различны и вершина
различны и вершина 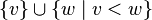 .
.
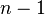 ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда
ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда 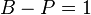 , где
, где  — число вершин,
— число вершин, 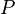 — число ребер графа.
— число ребер графа.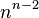 (Теорема Кэли о числе деревьев ).
(Теорема Кэли о числе деревьев ).