4.4.4. Представление выражений с помощью деревьев
С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу — операция. В общем случае дерево при этом может оказаться не бинарным.
Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным.
Рис.4.16. Представление арифметического выражения произвольного вида в виде дерева.
Рис. 4.17. Представление арифметического выражения в виде бинарного дерева
Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.
Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения.
Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным
Рис.4.18. Вычисление арифметического выражения с помощью бинарного дерева
Рис. 4.19. Представление логического выражения в виде бинарного дерева
4.5. Представление сильноветвящихся деревьев
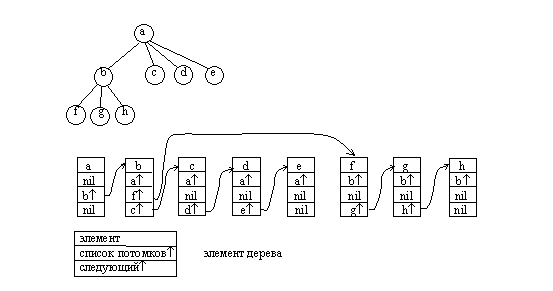
До сих пор мы рассматривали только способы представления бинарных деревьев. В ряде задач используются сильноветвящиеся деревья. Каждый элемент для представления бинарного дерева должен содержать как минимум три поля — значение или имя узла, указатель левого поддерева, указатель правого поддерева. Произвольные деревья могут быть бинарными или сильноветвящимися. Причем число потомков различных узлов не ограничено и заранее не известно.
Тем не менее, для представления таких деревьев достаточно иметь элементы, аналогичные элементам списковой структуры бинарного дерева. Элемент такой структуры содержит минимум три поля: значение узла, указатель на начало списка потомков узла, указатель на следующий элемент в списке потомков текущего уровня. Также как и для бинарного дерева необходимо хранить указатель на корень дерева. При этом дерево представлено в виде структуры, связывающей списки потомков различных вершин. Такой способ представления вполне пригоден и для бинарных деревьев.
Представление деревьев с произвольной структурой в виде массивов может быть основано на матричных способах представления графов.
Рис.4.20. Представление сильноветвящихся деревьев в виде списков
4.6. Применение сильноветвящихся деревьев
Один из примеров применения сильноветвящихся деревьев был связан с представлением арифметических выражений произвольного вида. Рассмотрим использование таких деревьев для представления иерархической структуры каталогов файловой системы. Во многих файловых системах структура каталогов и файлов, как правило, представляет собой одно или несколько сильноветвящихся деревьев. В файловой системе MS Dos корень дерева соответствует логическому диску. Листья дерева соответствуют файлам и пустым каталогам, а узлы с ненулевой степенью — непустым каталогам.
Рис.4.21. Представление логической структуры каталогов и файлов в виде сильноветвящегося дерева.
Для представления такой структуры используем расширение спискового представления сильноветвящихся деревьев. Способы представления деревьев, рассмотренные ранее, являются предельно экономичными, но не очень удобными для перемещения по дереву в разных направлениях. Именно такая задача встает при просмотре структуры каталогов. Необходимо осуществлять «навигацию» — перемещаться из текущего каталога в каталог верхнего или нижнего уровня, или от файла к файлу в пределах одного каталога.
Для облегчения этой задачи сделаем списки потомков двунаправленными. Для этого достаточно ввести дополнительный указатель на предыдущий узел «last». С целью упрощения перемещения по дереву от листьев к корню введем дополнительный указатель на предок текущего узла «up». Общими с традиционными способами представления являются указатели на список потомков узла «down» и следующий узел «next».
Для представления оглавления диска служат поля имя и тип файла/каталога. Рассмотрим программу, которая осуществляет чтение структуры заданного каталога или диска, позволяет осуществлять навигацию и подсчет места занимаемого любым каталогом.
Источник
Синтаксический разбор арифметических выражений
Рассмотрим арифметические выражения с обычным приоритетом операций. Сложение (+) и вычитание (—) имеют равный приоритет и более низкий (выполняются позже), чем умножение (*) с делением (/). Кроме этого, пусть существует унарный минус: -5, или -(3+5), или 3+-5=3+(-5). Несмотря на привычную операционную запись арифметических выражений, соответствующие действия являются функциями. Эти функции или бинарны (имеют два аргумента): plus(x, y) это «x+y» или унарны (один аргумент): inv(x) — это -(x).
Арифметическое выражение представимо в виде дерева. Например, дерево выражения 1*2 + 3*4 в корне имеет операцию сложения «+» и затем две ветви, в каждой из которых происходит умножение «*». В общем случае вызов вложенных друг в друга функций всегда образует дерево:
Будем описывать арифметическое выражение (функцию) типа op(lf, rt) при помощи структуры вида , где op — это тип операции, lf — первый аргумент, и rt — второй. Так, выражение 1*2+3*4 имеет следующее представление:
function Parser() < >Parser.calc = function (expr) < switch(expr.op)< case "N": // число (Number) return expr.lf; case "+" : // сложение return this.calc(expr.lf) + this.calc(expr.rt); case "-" : // вычитание return this.calc(expr.lf) - this.calc(expr.rt); case "*" : // умножение return this.calc(expr.lf) * this.calc(expr.rt); case "/" : // деление return this.calc(expr.lf) / this.calc(expr.rt); case "M" : // унарный минус (Minus) return -this.calc(expr.lf); >>
Результат работы этой функции с выражением 1*2+3*4 в виде структуры, приведенной выше, равен . Аналогичный вид имеет функция Parser.get(expr), которая печатает выражения в виде строки типа: .
Порождающая грамматика
Синтаксис арифметических выражений (с учетом приоритета операций) будем задавать следующей порождающей грамматикой:
E :- T1 + E | T1 - E | T1 T1 :- T2 * T1 | T2 / T1 | T2 T2 :- -T3 | T3 T3 :- N | (E)
Грамматика имеет смысл правил, по которым можно делать замены символов E, T1, T2, T3. В процессе таких замен происходит создание (порождение) некоторого арифметического выражения. Дерево начинает строиться с терма E (expression). Его можно заменить на одно из трех выражений (разделённых вертикальной чертой) из первой строки, например на: T1 + E. Затем необходимо сделать две замены для T1 и E, например (T2*T1) + T1. Далее, (T3*T2) + T2 и т.д., пока не доберёмся до числа N, на котором порождение останавливается.
Правила первой строки могут порождать цепочки T1 + T1 + T1 или T1 + T1 — T1 произвольной длины. Повторение терма E в конце правила E :- T1 + E образует «хвостовую» рекурсию, которая и генерит эти цепочки. Аналогичная хвостовая рекурсия стоит в правилах второй строки, определяющей структуру каждого слагаемого. Это даёт выражения вида T2*T2/T2*T2. Будем считать, что операции в таких цепочках выполняются слева направо: T2*(T2/(T2*T2)).
Фактически три терма T1,T2,T3 соответствуют трём уровням приоритета для операций (+ —), (* /) и унарного минуса (—). Подстановка правила T3 :- (E) из последней строки порождает вложенные скобки (..(..)..) любой глубины.
Вещественное число NUM также можно описать при помощи порождающей грамматики:
N :- I.I | I I :- D I | D D :- 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Впрочем, это делать не обязательно и стоит воспользоваться средствами JS для конверации строки в число.
Генерация случайных выражений
В качестве демонстрации порождения арифметических выражений при помощи грамматики, напишем четыре функции. Результаты 10 вызовов функции getRandE(5) приведены справа (их можно пересчитать, нажатием кнопки Recalc ):
Parser.getRandE = function (max) < switch(max-- >0 ? MS.rand(3): 0) < case 0: return this.getRandT1(max); // T1 case 1: return this.getRandT1(max)+"+"+this.getRandE(max); // T1+E case 2: return this.getRandT1(max)+"-"+this.getRandE(max); // T1-E >> Parser.getRandT1 = function (max) < switch(max-- >0 ? MS.rand(3): 0) < case 0: return this.getRandT2(max); // T2; case 1: return this.getRandT2(max)+"*"+this.getRandT1(max); // T2*T1 case 2: return this.getRandT2(max)+"/"+this.getRandT1(max); // T2/T1 >> Parser.getRandT2 = function (max) < if( MS.rand(10) ) return this.getRandT3(max); // T3; return "-"+this.getRandT3(max); // -T3; >Parser.getRandT3 = function (max) < if(max-- >0 ? MS.rand(10): 0) return "("+this.getRandE(max)+")"; // (E) return MS.rand(100); // N > Функция MS.rand(3) возвращает равновероятно 0,1 или 2, т.е. MS.rand(n) равна Math.floor(Math.random()*n). Параметр max устраняет очень длинные рекурсии. После каждого вызова он уменьшается и, когда достигает нуля, вызываются «нерекурсивные» грамматические правила. Функции getRandT2 и getRandT3 несколько отличаются и уменьшают вероятность унарного минуса и повышают вероятность появления скобок.
Символы вне грамматики
В арифметическом выражении будем допускать пробельные символы и комментарии:
// строчные (до конца строки) /* блочные - между этими символами */
Как и всё остальное, их можно описать при помощи грамматики, но эффективнее игнорировать эти символы на этапе сканирования строки. Проще всего использовать регулярные выражения:
st = st.replace(/\/\/.*/g, " "); // удаляем строчные комментарии (. - любой, кроме \n) st = st.replace(/\/\*[\s\S]*?\*\//g, ""); // удаляем блочные комментарии (нет вложений!) st = st.replace(/\s+/g, ""); // удаляем переносы строк и лишние пробелы
Однако это способ лишает возможности указывать в исходной строке положение синтаксических ошибок (если таковые присутствуют). Поэтому, напишем более громоздкую функцию пропуска незначимых для выражения символов, которая не изменяет строки.
Если комментариев нет — достаточно следующей функции:
function Parser() < this.n = 0; // текущее полжение при парсинге в строке >Parser.skip = function (st) < // пропускаем пробелы while(this.n < st.length && " \t\n\r".indexOf(st.charAt(this.n)) >= 0 ) this.n++; return (this.n
Текущее положение анализатора в строке хранится в переменной Parser.n. Функция Parser.skip(st) принимает строку st и возвращает новое положение, после пропуска (начиная с Parser.n) всех пробельных символов (меняя в себе Parser.n). При дохождении до конца строки, она возвращает -1.
Если есть комментарии, то функцию необходимо усложнить:
Parser.skip = function (st) < while(this.n < st.length && " \t\n\r".indexOf(st.charAt(this.n)) >= 0 ) this.n++; // пропускаем пробелы if(this.n >= st.length) return -1; // достигли конца строки if(st.charAt(this.n)===»/» && this.n+1 < st.length)< // возможны комментарии: if(st.charAt(this.n+1)==="/")< // строчный this.n += 2; while(this.n < st.length && st.charAt(this.n)!=="\n" ) this.n++; return this.skip(st); // вские \r и пробелы в начале след. >if(st.charAt(this.n+1)===»*») < // блочный this.n += 2; while(this.n+1 < st.length && (st.charAt(this.n) !== "*" || st.charAt(this.n+1) !== "\/")) this.n++; this.n += 2; return this.skip(st); // пробелы после комментариев >> return (this.n
Чтобы её протестировать, создадим два элемента textarea с соответствующими id и напишем следующий код:
var st1 = document.getElementById('skip_src_id').value; var st2 = ""; Parser.n = 0; while( Parser.skip(st1) >= 0 ) st2 += st1.charAt(Parser.n++); document.getElementById('skip_des_id').value = st2; Отметим, что функция Parser.skip не устраняет вложенные комментарии /* /* */ */. Для этого её необходимо модифицировать, подсчитывая число открывающихся (/*) и закрывающихся (*/) скобок. Впрочем, для языков, поддерживающих строки, необходимо учесть наличие таких последовательностей внутри строк, например: /* » /*» */. Поэтому ограничимся запретом вложенных комментариев.
Синтаксический разбор
Перейдём теперь к синтаксическому разбору строки, в результате которого получится дерево выражения. Стартом для парсинга будет служить функция:
Она обнуляет указатель this.n (текущее положение в анализируемой строке) и очищает строку с описанием синтаксических ошибок this.err. Затем вызывается функция парсинга терма E, реализующего грамматику E :- T1 + E | T1 — E | T1
Parser.parseE = function (st) < var t1 = this.parseT1(st); // вычитываем терм T1 if(this.skip(st) < 0) // пропускаем пробелы и комметарии return t1; // E :- T1 (в конце строки) switch(st.charAt(this.n))< case "+": // E :- T1 + E this.n++; return ; case "-": // E :- T1 - E this.n++; return ; > this.err += "\nn="+this.n+"> parseE: no + or - after term T1"; return t1; // вернём undefined >
После прочтения терма T1, выясняется наличие арифметических знаков + — и, если они есть, читается второй терм, который снова парсится функцией Parser.parseE (хвостовая рекурсия). Ошибка err будет генериться, например, для выражения вида «2 2».
Аналогично выглядит функция парсинга терма T1 :- T2 * T1 | T2 / T1 | T2:
Parser.parseT1 = function (st) < var t2 = this.parseT2(st); // вычитываем терм T2 if(this.skip(st) < 0) // пропускаем пробелы и комметарии return t2; // T1 :- T2 (в конце строки) switch(st.charAt(this.n))< case "*": this.n++; // T1 :- T2 * T1 return ; case "/": // T1 :- T2 / T1 this.n++; return ; > return t2; // T1 :- T2 (нет * или /) >
Здесь уже нет обработки синтаксической ошибки, так как после терма T2 не обязательно идёт операция «*» или «/» (может быть «+», «-«).
Похожа и функция для терма Т2, которая выделяет унарный минус. В предыдущих функциях пропуск пробелов в самом начале не вызывался, так как предполагалось, что это сделает Parser.parseT2(st), которая не может применяться к пустому терму. В результате строки типа «2+» сгенерят ошибку.
Parser.parseT2 = function (st) < if(this.skip(st) < 0)< this.err += "\nn="+this.n+">parseT2: empty term"; return; > if(st.charAt(this.n) === "-") < this.n++; return ; // T2 :- -T3 > return this.parseT3(st); // T2 :- T3 >
Самой громоздкой оказывается функция парсинга последнего терма, которая должна вычитать вещественное число и убедиться, что открытая скобка в правиле «T3:-(E)» закрывается. В результате она имеет три точки в которых происходит генерация сообщения об ошибке. Эта функция использует функцию isdigit(st, n), возвращающую st.charAt(n)>=»0″ && st.charAt(n) Recalc :
Источник