Динамические структуры данных: бинарные деревья
Аннотация: В лекции рассматриваются определения, свойства и виды деревьев, элементы, характеристики и способы объявления деревьев в программах, основные операции над элементами деревьев, понятие и виды обходов деревьев, приводятся примеры реализации основных операций над бинарными деревьями в виде рекурсивных функций.
Цель лекции: изучить понятие, формирование, особенности доступа к данным и работы с памятью в бинарных деревьях, научиться решать задачи с использованием рекурсивных функций и алгоритмов обхода бинарных деревьев в языке C++.
Дерево является одним из важнейших и интересных частных случаев графа. Древовидная модель оказывается довольно эффективной для представления динамических данных с целью быстрого поиска информации .
Деревья являются одними из наиболее широко распространенных структур данных в информатике и программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.
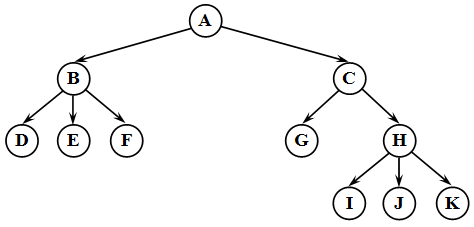
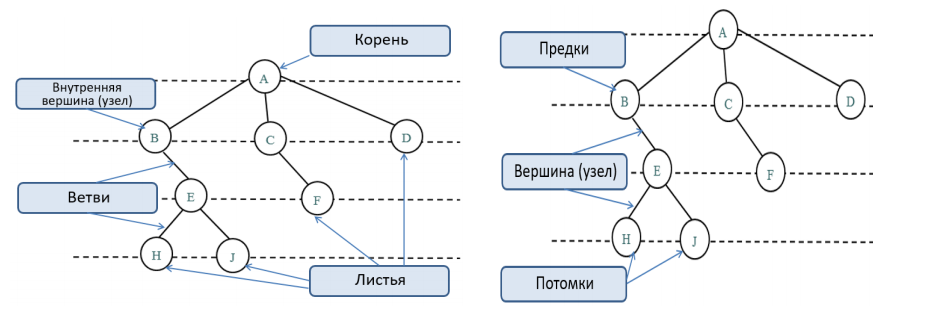
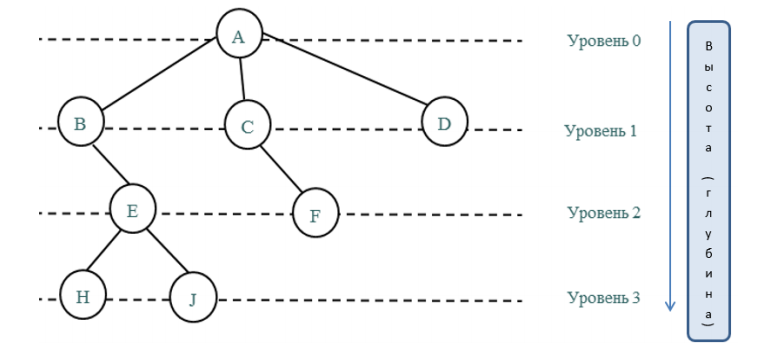
Дерево – это структура данных , представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов ( рис. 31.1). Каждый элемент дерева называется вершиной (узлом) дерева. Вершины дерева соединены направленными дугами, которые называют ветвями дерева. Начальный узел дерева называют корнем дерева, ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.
Каждое дерево обладает следующими свойствами:
- существует узел, в который не входит ни одной дуги (корень);
- в каждую вершину, кроме корня, входит одна дуга.
Деревья особенно часто используют на практике при изображении различных иерархий. Например, популярны генеалогические деревья.
Все вершины, в которые входят ветви, исходящие из одной общей вершины, называются потомками, а сама вершина – предком. Для каждого предка может быть выделено несколько. Уровень потомка на единицу превосходит уровень его предка. Корень дерева не имеет предка, а листья дерева не имеют потомков.
Высота (глубина) дерева определяется количеством уровней, на которых располагаются его вершины. Высота пустого дерева равна нулю, высота дерева из одного корня – единице. На первом уровне дерева может быть только одна вершина – корень дерева , на втором – потомки корня дерева, на третьем – потомки потомков корня дерева и т.д.
Поддерево – часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.
Степенью вершины в дереве называется количество дуг, которое из нее выходит. Степень дерева равна максимальной степени вершины, входящей в дерево . При этом листьями в дереве являются вершины, имеющие степень нуль. По величине степени дерева различают два типа деревьев:
Упорядоченное дерево – это дерево , у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.
Деревья являются рекурсивными структурами, так как каждое поддерево также является деревом. Таким образом, дерево можно определить как рекурсивную структуру, в которой каждый элемент является:
Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.
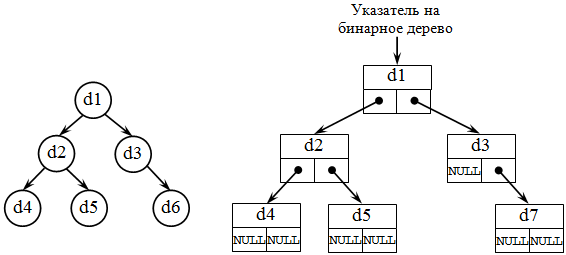
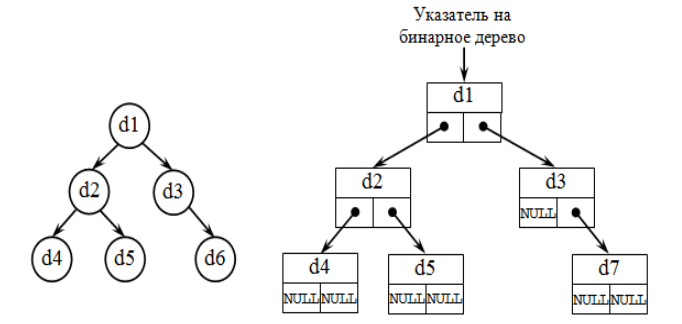
Списочное представление деревьев основано на элементах, соответствующих вершинам дерева. Каждый элемент имеет поле данных и два поля указателей: указатель на начало списка потомков вершины и указатель на следующий элемент в списке потомков текущего уровня. При таком способе представления дерева обязательно следует сохранять указатель на вершину, являющуюся корнем дерева .
Для того, чтобы выполнить определенную операцию над всеми вершинами дерева необходимо все его вершины просмотреть. Такая задача называется обходом дерева.
Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.
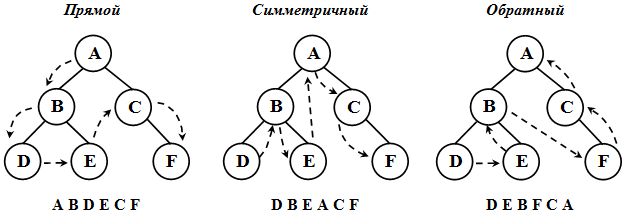
При обходе все вершины дерева должны посещаться в определенном порядке. Существует несколько способов обхода всех вершин дерева. Выделим три наиболее часто используемых способа обхода дерева ( рис. 31.2):
Существует большое многообразие древовидных структур данных. Выделим самые распространенные из них: бинарные (двоичные) деревья, красно-черные деревья, В-деревья, АВЛ-деревья , матричные деревья, смешанные деревья и т.д.
Бинарные деревья
Бинарные деревья являются деревьями со степенью не более двух.
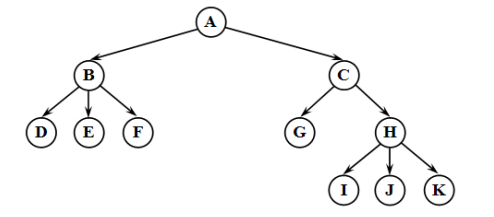
Бинарное (двоичное) дерево – это динамическая структура данных , представляющее собой дерево , в котором каждая вершина имеет не более двух потомков ( рис. 31.3). Таким образом, бинарное дерево состоит из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка .
Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут соответственно:
- информационное поле (ключ вершины);
- служебное поле (их может быть несколько или ни одного);
- указатель на левое поддерево ;
- указатель на правое поддерево .
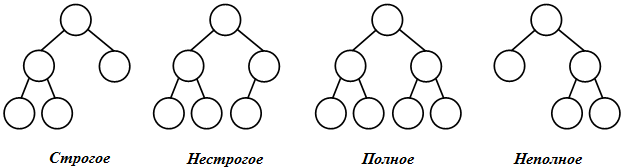
По степени вершин бинарные деревья делятся на ( рис. 31.4):
- строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
- нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).
В общем случае у бинарного дерева на k -м уровне может быть до 2 k-1 вершин. Бинарное дерево называется полным, если оно содержит только полностью заполненные уровни. В противном случае оно является неполным.
Дерево называется сбалансированным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.
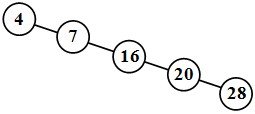
Бинарное дерево может представлять собой пустое множество . Бинарное дерево может выродиться в список ( рис. 31.5).
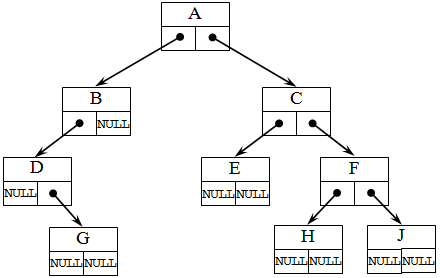
Структура дерева отражается во входном потоке данных так: каждой вводимой пустой связи соответствует условный символ, например, ‘*’ (звездочка). При этом сначала описываются левые потомки, затем, правые. Для структуры бинарного дерева , представленного на следующем рисунке 6, входной поток имеет вид: ABD*G***CE**FH**J** .
Бинарные деревья могут применяться для поиска данных в специально построенных деревьях ( базы данных ), сортировки данных, вычислений арифметических выражений , кодирования (метод Хаффмана) и т.д.
Источник
Дерево как структура данных
Какую выгоду можно извлечь из такой структуры данных, как дерево? В этой статье мы расскажем о данных в виде дерева, рассмотрим основные определения, которые следует знать, а также узнаем, как и зачем используется дерево в программировании. Спойлер: бинарные деревья часто применяют для поиска информации в базах данных, для сортировки данных, для проведения вычислений, для кодирования и в других случаях. Но давайте обо всем по порядку.
Основные термины
Дерево — это, по сути, один из частных случаев графа. Древовидная модель может быть весьма эффективна в случае представления динамических данных, особенно тогда, когда у разработчика стоит цель быстрого поиска информации, в тех же базах данных, к примеру. Еще древом называют структуру данных, которая представляет собой совокупность элементов, а также отношений между этими элементами, что вместе образует иерархическую древовидную структуру.
Каждый элемент — это вершина или узел дерева. Узлы, соединенные направленными дугами, называются ветвями. Начальный узел — это корень дерева (корневой узел). Листья — это узлы, в которые входит 1 ветвь, причем не выходит ни одной.
Общую терминологию можно посмотреть на левой и правой части картинки ниже:
Какие свойства есть у каждого древа:
— существует узел, в который не входит ни одна ветвь;
— в каждый узел, кроме корневого узла, входит 1 ветвь.
На практике деревья нередко применяют, изображая различные иерархии. Очень популярны, к примеру, генеалогические древа — они хорошо известны. Все узлы с ветвями, исходящими из единой общей вершины, являются потомками, а сама вершина называется предком (родительским узлом). Корневой узел не имеет предков, а листья не имеют потомков.
Также у дерева есть высота (глубина). Она определяется числом уровней, на которых располагаются узлы дерева. Глубина пустого древа равняется нулю, а если речь идет о дереве из одного корня, тогда единице. В данном случае на нулевом уровне может быть лишь одна вершина – корень, на 1-м – потомки корня, на 2-м – потомки потомков корня и т. д.
Ниже изображен графический вывод древа с 4-мя уровнями (дерево имеет глубину, равную четырем):
Следующий термин, который стоит рассмотреть, — это поддерево. Поддеревом называют часть древообразной структуры, которую можно представить в виде отдельного дерева.
Идем дальше. Древо может быть упорядоченным — в данном случае ветви, которые исходят из каждого узла, упорядочены по некоторому критерию.
Степень вершины в древе — это число ветвей (дуг), выходящих из этой вершины. Степень равняется максимальной степени вершины, которая входит в дерево. В этом случае листьями будут узлы, имеющие нулевую степень. По величине степени деревья бывают:
— двоичные (степень не больше двух);
— сильноветвящиеся (степень больше двух).
Деревья — это рекурсивные структуры, ведь каждое поддерево тоже является деревом. Каждый элемент такой рекурсивной структуры является или пустой структурой, или компонентом, с которым связано конечное количество поддеревьев.
Когда мы говорим о рекурсивных структурах, то действия с ними удобнее описывать посредством рекурсивных алгоритмов.
Обход древа
Чтобы выполнить конкретную операцию над всеми вершинами, надо все эти узлы просмотреть. Данную задачу называют обходом дерева. То есть обход представляет собой упорядоченную последовательность узлов, в которой каждый узел встречается лишь один раз.
В процессе обхода все узлы должны посещаться в некотором, заранее определенном порядке. Есть ряд способов обхода, вот три основные:
— прямой (префиксный, preorder);
— симметричный (инфиксный, inorder);
— обратный (постфиксный, postorder).
Существует много древовидных структур данных: двоичные (бинарные), красно-черные, В-деревья, матричные, смешанные и пр. Поговорим о бинарных.
Бинарные (двоичные) деревья
Бинарные имеют степень не более двух. То есть двоичным древом можно назвать динамическую структуру данных, где каждый узел имеет не большое 2-х потомков. В результате двоичное дерево состоит из элементов, где каждый из элементов содержит информационное поле, а также не больше 2-х ссылок на различные поддеревья. На каждый элемент древа есть только одна ссылка.
У бинарного древа каждый текущий узел — это структура, которая состоит из 4-х видов полей. Какие это поля:
— информационное (ключ вершины);
— служебное (включена вспомогательная информация, однако таких полей может быть несколько, а может и не быть вовсе);
— указатель на правое поддерево;
— указатель на левое поддерево.
Самый удобный вид бинарного древа — бинарное дерево поиска.
Что значит древо в контексте программирования?
Мы можем долго рассуждать о математическом определении древа, но это вряд ли поможет понять, какие именно выгоды можно извлечь из древовидной структуры данных. Тут важно отметить, что древо является способом организации данных в форме иерархической структуры.
В каких случаях древовидные структуры могут быть полезны при программировании:
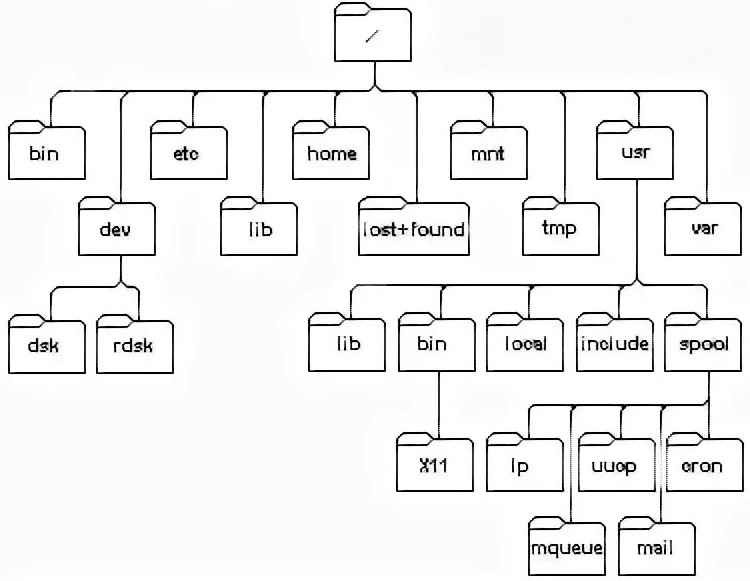
- Когда данная иерархия существует в предметной области разрабатываемой программы. К примеру, программа должна обрабатывать генеалогическое древо либо работать со структурой каталогов. В таких ситуациях иногда есть смысл сохранять между объектами программы существующие иерархические отношения. В качестве примера можно вывести древо каталогов операционной системы UNIX:
- Когда между объектами, которые обрабатывает программа, отношения иерархии не заданы явно, но их можно задать, что сделает обработку данных удобнее. Как тут не вспомнить разработку парсеров либо трансляторов, где весьма полезным может быть древо синтаксического разбора?
- А сейчас очевидная вещь: поиск объектов более эффективен, когда объекты упорядочены, будь то те же базы данных. К примеру, поиск значения в неструктурированном наборе из тысячи элементов потребует до тысячи операций, тогда как в упорядоченном наборе может хватить всего дюжины. Вывод прост: раз иерархия — эффективный способ упорядочивания объектов, почему же не использовать древовидную иерархию для ускорения поиска узлов со значениями? Так и происходит: если вспомнить бинарные деревья, то на практике их можно применять в следующих целях:
— поиск данных в базах данных (специально построенных деревьях);
— сортировка и вывод данных;
— вычисления арифметических выражений;
— кодирование по методу Хаффмана и пр.
Источник