Дерево это двудольный граф

Определение и свойства деревьев.

Деревом называется произвольный связный граф без циклов. Деревья обладают следующими свойствами:

любые две вершины соединены единственной простои цепью

количество ребер на единицу меньше количества вершин

при удалении любого ребра дерево становится не связным графом

при добавлении к дереву любого ребра в дереве появляется ровно один простой цикл.

Фактически дерево можно получить из любого связного графа

Утверждение: любой связный граф содержит остовный подграф который является деревом. Этот подграф называется остовыным деревом.

Специальные виды деревьев

1 Корневые деревья

Определение: Корневое дерево — ориентированное дерево, которое удовлетворяет условиям:

a) Имеется ровно один узел в который не входит не одно

В каждый узел кроме корня входит ровно одно ребро

Из корня имеется путь к любому ребру.

Если имеется путь от вершины vl к вершине v2, тогда вершина vl предок вершины v2, а вершина v2 потомок вершины vl.

Вершина которая не имеет потомков называется концевой вершиной или листом. Не концевую вершину называют внутренней. Если V₁ и V₂ дуга корневого дерева, то V₁— отец, a V₂— сын

Глубина дерева — длина пути из корня. Узлы находящиеся на одной глубине называются ярусами дерева.

Для задания корневого дерева можно использовать те же способы, что и для любого графа. На практике для представления деревьев используется канонический способ: для каждого узла хранится указатель на отца.

2 Бинарные деревья

Определение: Бинарное дерево — корневое дерево у каждой вершины которого не более двух сыновей.

В таком дереве любой произвольный узел имеет левого и правого сына. Поддерево корнем которого является левый сын называется левым поддеревом. Поддерево корнем которого является правый сын называется правым поддеревом.

Имеется два способа представления бинарных деревьев:

1. Представление в виде двух массивов: первый массив- левые сыновья, второй — правые.

2. Представление в виде списковой структуры tree_ ptr Tree_mode — запись имеющая структуру:

Element- тип узла; Left: tree_ ptr; Right: tree_ ptr;

3 Полные бинарные деревья

Определение: Полное бинарное дерево — бинарное дерево для которого выполняются условия:

a) Заполнение дерева осуществляется от корня к листьям по уровням.

b) Заполнение уровней осуществляется слева направо.

Полные бинарные деревья представляются в виде одномерного массива: первый элемент массива — корень дерева. Для любого i-того узла элемент с индексом (2i) — левый сын, элемент с индексом (2i+l)- правый сын. Отец узла j — (j/2).

4 Бинарные поисковые деревья

Определение: Бинарное поисковое дерево — дерево поиска,

Все ключи в левом поддереве меньше ключа узла V

В правом поддереве все ключи больше, чем ключ V

В дереве нет одинаковых ключей.

5 Сбалансированные деревья

Определение: Дерево называется идеально сбалансированным, если оно является бинарным поисковым деревом и число вершин его левых и правых поддеревьев отличается не более, чем на единицу.

Определение: Дерево называется сбалансированным, если оно бинарное поисковое и высоты двух поддеревьев в каждой из вершин отличаются не более, чем на единицу.

6 Способы обхода узлов в бинарных деревьях

Большинство алгоритмов при работе с деревьями посещают каждый узел в некотором порядке.

Существует три наиболее распространенных способа обхода деревьев:

1. Прямой порядок: корень посещается раньше, чем поддеревья

Порядок обхода: корень — левое поддерево — правое поддерево.

Процедура организуется рекурсивно.

2. Обратный порядок (снизу вверх): корень посещается после поддеревьев.

Порядок обхода: левое поддерево — правое поддерево- корень.

3. Внутренний порядок (слева направо )

Порядок обхода: левое поддерево – корень — правое поддерево.

7 Представление множеств с помощью деревьев

Базовыми операциями над множествами являются:

определение принадлежности элемента множества.

объединение не пересекающихся множеств.

Каждое множество будем представлять в виде корневого дерева. Корень дерева можно использовать для хранения имени множества. Дерево будем представлять в каноническом виде.

Чтобы определить, к какому множеству принадлежит некоторый элемент — находим этот элемент и определяем корень множества, к которому он принадлежит. Этот корень — есть имя искомого множества.

Объединение непересекающихся множеств можем реали­зовать тремя способами:

Источник

Деревья и двудольные графы

В двудольном граф циклы, если они есть, имеют чётную длину. Дерево – это связный двудольный граф (без циклов, естественно) Если доли вершин двудольного графа перемешаны, то можно по рисунку графа эти доли определить. Надо взять любую вершину и пометить её, как принадлежащую к первой доле (буквой А, например). Тогда все смежные к этой вершине вершины будут из второй доли (буква Б), и, в свою очередь, смежные к вершинам второй доли вершины будут из первой доли, и так далее. Таким же способом можно определять и «двудольность» произвольного графа. Если вершины одной доли смежны, то это не двудольный граф.

Любое дерево может быть задано его двоичным кодом. Код дерева имеет длину 2mи состоит изmнулей иmединиц. Для любого начального отрезка кода дерева число единиц в нём не больше числа нулей. Код дерева всегда начинается с 0 и заканчивается 1. Код дерева зависит от того, какую вершину мы выберем в качестве корня. Дерево с одним ребром и двумя вершинами имеет код 01. Каждое ребро дерева имеет в коде свой ноль и свою единицу, причем единица всегда находится в коде далее нуля. Код получается в результат обхода дерева. Обход начинается и заканчивается в корне дерева. Если ребро дерева встречается при обходе первый раз, то в коде появляется 0 этого ребра, а если второй (и последний), то в коде появляется 1 этого ребра. Например, цепочка из 5 вершин (C) является простейшим деревом и имеет код 00001111.

Колесо с nвершинами (W) имеет одну вершину степениn-1 в центре (ось колеса) иn-1 вершину степени три по окружности колеса. У колеса есть спицы (рёбра, выходящие из оси колеса)..W=K, например, (тетраэдр).

Число Каталана – это число бинарных деревьев с nвершинами. Бинарное дерево сn=0 – это пустое дерево, а сn>0 вершинами – это тройка Д=(Л, К, П), где К – вершина, называемая корнем дерева, Л – левое поддерево с Л вершинами и П – правое поддерево с П вершинами иn=Л+1+П. С— число различных бинарных деревьев сkвершинами (число Каталана).C=C=1 и если 0Cразличных бинарных деревьев вида (s, К,k-1-s). s принимает значения от 0 доk-1, и, значит, С=CС+CС+ . . . + СCиk>0. С помощью производящей функции получается, что С=C/(k+1).

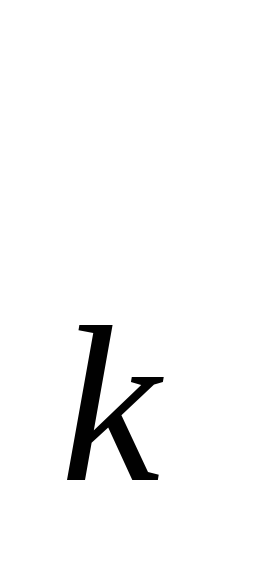
Остовное дерево связного графа содержит все его вершины и некоторые рёбра. Для получения остовного дерева в графе находят цикл и убирают из него произвольное ребро. Затем опять находят цикл и убирают ребро, пока циклов в графе не останется. Остовных деревьев может быть несколько. Цикломатическое число графа – это число рёбер, которые надо удалить из графа, чтобы превратить граф в лес (в дерево, если граф связен).=p+m-n. Цикломатическое число леса (и дерева) равно нулю.

Задания по деревьям и двудольным графам

Определить число попарно различных двудольных графов с а) n=6 m=8; б) n=5 m=9; в) n1=3 n2=4 m=9. n=n1+n2

Доказать, что существует ровно 6 неизоморфных деревьев с 6 вершинами и 11 – с 7 вершинами.

Доказать, что во всяком дереве с n>1 вершинами содержится не менее 2 висячих вершин.

Пусть n1 – число висячих вершин n-вершинного дерева, не содержащего вершин степени 2. Доказать, что n1>n/2.

Индукцией по n доказать, что каждое дерево с n>1 вершинами является двудольным графом. Какие деревья являются полными двудольными графами?

Изобразить все попарно неизоморфные деревья: а) с 6 рёбрами и 3 висячими вершинами; б) с 6 рёбрами и 4 висячими вершинами; в) с 7 рёбрами и 3 висячими вершинами; г) с 8 рёбрами и 3 вершинами степени 3.

Подсчитать число попарно неизоморфных 7-вершинных деревьев, у которых сумма квадратов степеней вершин меньше 27.

Существуют ли двудольные кубические (регулярные, степени 3) графы? Нарисовать, если да. Может ли быть различным число вершин в долях в регулярном двудольном графе?

Если графы G и H (без петель и кратных рёбер) изоморфны, то для каждого d>-1 число вершин степени d в графах G и H одинаково. Показать, что а) это условие (подчёркнуто выше) является достаточным для изоморфизма графов с 4 и менее вершинами; б) условие не является достаточным для изоморфизма графов с 5 и более вершинами, причём, если число вершин не менее 6, то даже для деревьев.

Описать и нарисовать все графы, являющиеся деревьями вместе со своими дополнениями.

Построить все попарно неизоморфные растущие деревья (в них существует источник с полустепенью захода, равной нулю) с а) 4 вершинами; б) 5 вершинами; в) 6 вершинами, не содержащие ориентированных цепей длины, превосходящей 3.

Доказать, что слабо связный орграф является растущим деревом (в нём существует источник с полустепенью захода, равной нулю) тогда и только тогда, когда лишь одна его вершина имеет нулевую полустепень захода, а полустепень захода любой из остальных вершин равна 1.

Построить дерево по его коду: а) 0010100111; б) 00110101000111; в) 0000010011011111;

По вектору установить, является ли он кодом дерева (если да, то построить дерево): а) 001011; б) 110 0110; в) 001001; г) 010011; д) 00111001; е) 0001100111.

Доказать по индукции, что для каждого дерева в его коде число нулей совпадает с числом единиц, и число единиц среди первых k координат кода (km) не превосходит числа нулей среди тех же координат. Длина кода дерева равна 2m, где m – число рёбер в дереве.

Длина кода дерева равна 2m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: а) f(m)+1; б)f(m)+1; в) f(m)+1.

Длина кода дерева равна 2m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: f(m)=. f(0)=f(1)=1

Вершина корневого дерева называется висячей,

если она отлична от корня и имеет степень, равную 1. а) у дерева k висячих вершин и нет вершин степени 2, отличных от корня. Доказать, что при k>1 n

Диаметр дерева – длина максимальной простой цепи в нём. Доказать, что в дереве с нечётным диаметром любые две простые цепи максимальной длины имеют хотя бы общее ребро. А с чётным?

Доказать, что некорневое дерево однозначно с точностью до изоморфизма восстанавливается, если заданы все попарные расстояния между его висячими вершинами.

Расстояние между вершинами – это длина кратчайшей цепи, соединяющей их. Диаметр графа – это max расстояний в нём. а) для каждого d>2 указать граф, диаметр которого равен d, а диаметр любого его связного остовного (содержащего все вершины графа) дерева равен 2d.

Вычислить цикломатическое число а) полного графа с n вершинами (K); б) полного двудольного графа сn1 и n2 вершинами в долях (K); в) пустого графа сn вершинами (n изолированных вершин — N); г) колеса сn вершинами (W); д) платоновых графов: тетраэдра (K), куба, октаэдра, додекаэдра; е) графа Петерсена; ж) любого связного регулярного степениr (степени всех вершин равны r) графа с n вершинами.

Остовное дерево графа содержит все вершины графа и некоторые его рёбра. Найти остовное дерево: а) полного графа с 5 вершинами (K); б) полного двудольного графа с тремя вершинами в каждой из долей (K); в) колеса с 5 вершинами (W); г) циклического графа с 6 вершинами (C); д) графа Петерсена; е) платоновых графов: тетраэдра (K), куба, октаэдра, додекаэдра.

Остовное дерево графа содержит все вершины графа и некоторые его рёбра. Пусть T1 и T2 – остовные деревья графа G. Доказать, что для каждого ребра e из T1 существует ребро f из T2, и если в T1 заменить e на f, то получим опять остовное дерево графа G. Доказать, что T1 можно перевести в T2 , меняя по очереди рёбра из T1 на рёбра из T2.

Приведите примеры (когда это возможно) а) регулярного (степени всех вершин равны) двудольного графа; б) двудольного платонова графа (тетраэдр (K), куб, октаэдра, додекаэдр); в) бесконечного двудольного графа.

Что можно сказать о дополнении полного двудольного графа? Дополнение графа – это граф с те ми же вершинами и с рёбрами, которых нет в самом графе. Опишите матрицу смежности двудольного графа. Что можно сказать о матрицах смежности двудольного графа и его дополнения?

Люди – это вершины, а знакомых людей связывает ребро. Доказать, что среди 6 человек всегда найдутся 3 таких, которые либо все знают друг друга (цикл длины 3), либо ни один из них не знает двух других.

G – двудольный граф с наибольшей степенью вершин d. Покажите, что существует двудольный граф G1(v1,v2), в котором v1 и v2 содержат одинаковое число вершин и G1 — регулярный граф степени d, причём G – это подграф G1. Показать алгоритм построения G1 из G.

Расстояние между вершинами – это длина кратчайшей цепи, соединяющей их. Диаметр графа – это max расстояний в нём. Диаметр дерева – длина максимальной простой цепи в нём. Доказать, что для каждого связного графа существует его остовное дерево, диаметр которого не более чем в два раза превосходит диаметр графа.

Источник