Дерево Фенвика
Дерево Фенвика или двоичное индексированное дерево (англ. binary indexed tree) — структура данных, которая на многих задачах заменяет собой дерево отрезков, но при этом работает в 3-4 раза быстрее, занимает минимально возможное количество памяти (столько же, сколько и массив той же длины), намного быстрее пишется и легче обобщается на большие размерности.
Определение
Пусть дан массив \(a\) длины \(n\) . Деревом Фенвика будем называть массив \(t\) той же длины, объявленный следующим образом:
где \(F\) это какая-то функцию, для которой выполнено \(F(i) \leq i\) . Конкретно её определим потом.
Запрос суммы. Когда нам нужна сумма на отрезке, мы будем сводить этот запрос к двум суммам на префиксе: \(sum(l, r) = sum(r) — sum(l-1)\) . Оба этих запроса будем считать по формуле:
Запрос обновления. Когда мы изменяем \(k\) -ю ячейку исходного массива, мы обновляем все \(t_i\) , в которых учтена эта ячейка.
\(F\) можно выбрать так, что и «спусков» при подсчете суммы, и интересных нам \(t_i\) при обновлении будет будет \(O(\log n)\) . Популярны две функции:
Первый вариант описан на Викиконспектах и Емаксе и поэтому более известен. Второй, как мы дальше увидим, более простой для запоминания и кодинга, а так же более гибкий — например, там можно делать бинпоиск по префиксным суммам. Его мы и будем использовать.
Примечание. Наверное, меньше четверти умеющих писать эту структуру полностью понимают, как она работает. Анализ действительно весьма сложный, поэтому мы приведём его в конце. Рекумендуется пока что абстрагироваться и принять на веру, что любой префикс разбивается на \(O(\log n)\) отрезков вида \([F(i), i]\) , а также что любой элемент входит в не более \(O(\log n)\) таких отрезков.
Реализация
Так как \(F(0) = 1 > 0\) , то \([0, F(0)]\) не является корректным отрезком. Поэтому нам будет удобнее хранить массив в 1-индексации и не использовать \(t_0\) .
int t[maxn]; // возвращает сумму на префиксе int sum (int r) int res = 0; for (; r > 0; r -= r & -r) res += t[r]; return res; > int sum (int l, int r) return sum(r) - sum(l-1); > // обновляет нужные t void add (int k, int x) for (; k n; k += k & -k) t[k] += x; >Автор отмечает красивую симметрию в формулах r -= r & -r и k += k & -k , которой нет в «традиционной» версии.
Многомерный случай
\(k\) -мерное дерево Фенвика пишется в \((k+1)\) строчку
Нужно добавить всего одну такую же строчку в sum , add , а также при подсчете суммы на прямоугольнике вместо двух запросов к префиксным суммам использовать четыре.
sum перепишется следующим образом:
int sum (int r1, int r2) int res = 0; for (int i = r1; i > 0; i -= i & -i) for (int j = r2; j > 0; j -= j & -j) ans += t[i][j]; return res; >В \(k\) -мерном случае, в соответствии с принципом включений-исключений, для запроса суммы нужно \(2^k\) запросов суммы на префиксах.
Если размерности больше, чем позволяет память, то можно вместо массива t использовать хэш-таблицу — так потенциально потребуется \(O(q \log^2 A)\) памяти ( \(A\) — максимальная координата), но это всё равно один из самых безболезненных способов решать достаточно простые задачи на двумерные структуры. Автор в своё время таким образом решил какую-то задачу на 2d-сумму с USACO 2017.
Бинпоиск
Оказывается, можно производить бинарный поиск (точнее, спуск) по префиксным суммам за \(O(\log n)\) .
// возвращает индекс, на котором сумма уже больше int lower_bound (int s) int k = 0; for (int l = logn; l >= 0; l--) if (k + (1) n && t[k + (1)] s) k += (1); s -= t[k]; > > return k; >Если знать, что \(F(x)\) удаляет последний бит \(x\) , то принцип понятен: просто делаем спуск по бинарному дереву, как в ДО. Чем-то похоже на генерацию \(k\) -го лексикографического комбинаторного объекта: пытаемся увеличить следующий символ всегда, когда это возможно.
Отметим, что в «традиционной» индексации такое делать нельзя.
Ограничения на операцию
Дерево Фенвика можно использовать, когда наша операция обратима, а также когда трюк с префиксными суммами работает. Это обычно простые операции типа суммы, xor , умножения по модулю (если гарантируется, что на этот модуль ничего не делится). Минимум и gcd , отложенные операции и персистентность прикрутить в общем случае уже не получится — тогда уже нужно писать дерево отрезков.
Почему это работает
Итак, мы выбрали вариант с \(F(x)\) = x — (x & -x) + 1 . Поймем, что означает x & -x .
Лемма. x & -x возвращает последний единичный бит в двоичной записи x.
Доказательство потребует знания, как в компьютерах хранятся целые числа. Чтобы процессор не сжигал лишние такты, проверяя знак числа при арифметических операциях, их хранят как бы по модулю \(2^k\) , а первый бит отвечает за знак (0 для положительных и 1 для отрицательных). Поэтому когда мы хотим узнать, как выглядит отрицательное число, нужно его вычесть из нуля: \(-x = 0-x = 2^k-x\) .
Как будет выглядеть -x в битовой записи? Ответ можно мысленно разделить на три блока:
- Первые сколько-то (возможно, нисколько) нулей с конца числа x ими же в ответе и останутся.
- Потом, ровно на самом младшем единичном бите x, мы «займём» много единиц, так что весь префикс станет единицами. В ответе на этом месте точно будет единица.
- Потом отменятся ровно те биты из этого префикса, которые были единицами в исходном числе.
\[ \begin +90 = 2+8+16+64 & = 0 \, 10110_2 \\ -90 = 00000_2 — 10110_2 & = 1 \, 01010_2 \\ \implies (+90) \& (-90) & = 0 \, 00010_2 \\ \end \]
Теперь мы можем доказать нашу лемму. Когда мы сделаем &, в префиксе до младшего единичного бита все биты x и -x будут противоположными, младший единичный бит останется единичным, а на суффиксе все как было нулями, так и осталось. Следовательно, «выживет» только этот самый младший единичный бит, что мы и доказывали.
Следствие 1. sum будет работать за логарифм, а точнее за количество единичных битов в записи \(x\) : на каждой итерации мы делаем x -= x & -x , то есть удаляем младший бит.
Следствие 2. add тоже будет работать за логарифм: каждую итерацию количество нулей на конце \(x\) увеличивается хотя бы на единицу.
Следствие 3. (Почему дерево Фенвика — дерево.)
- Длина отрезка, соответствующего любому \(t_i\) — степень двойки, причём начинается этот отрезок на индексе, кратном этой же степени двойки.
- \(\implies\) Множества элементов, учтённых в произвольных \(t_i\) и \(t_j\) , либо не пересекаются, либо одно является подмножеством другого.
- \(\implies\) На \(t_i\) можно ввести отношение вложенности.
То есть, если напрячь воображение, то \(t\) можно рассматривать как лес деревьев. В частном случае, когда \(n\) является степенью двойки, дерево будет одно.
Теперь единственное, что осталось доказать — это корректность add . На самом деле, в add мы делаем ни что иное, как подъём от вершины до корня по всем предкам.
Как для \(x\) найти непосредственного родителя? Нужно найти минимальное число \(y > x\) , у которого \(t_y\) будет включать \(x\) . Иными словами, должно выполняться y >= x > y — (y & -y) .
Дальше читателю предлагается самостоятельно попялиться в пример, чтобы понять, что x + (x & -x) — минимальное такое число:
\[ \begin x = 90 = 2+8+16+64 & = 10110_2 \\ y = 96 = 32 + 64 & = 11000_2 \\ \end \]
Источник
Многомерное дерево Фенвика
Рассмотрим для начала дерево Фенвика на примере k-мерного массива с [math]k = 2[/math] , а затем посмотрим, как можно обобщить его на большие размерности.
Пусть дан массив [math] A [/math] из [math] n \times m [/math] элементов: [math] a_[/math] .
Деревом Фенвика будем называть массив [math] T [/math] из [math] n \times m [/math] элементов: [math] T_ = \sum\limits_^ \sum\limits_^a_[/math] , где [math]F(i) = i\; \&\; (i + 1)[/math] , как и в одномерном дереве Фенвика.
Пример задачи для двумерного случая
Пусть имеем набор точек на плоскости с неотрицательными координатами. Определены 3 операции:
- добавить точку в [math](x, y)[/math] ;
- удалить точку из [math](x, y)[/math] ;
- посчитать количество точек в прямоугольнике [math](0, 0), (x, y)[/math] ;
[math]n[/math] — количество точек, [math]maxX[/math] — максимальная [math]X[/math] координата, [math]maxY[/math] — максимальная [math]Y[/math] координата.
Тогда дерево строится за [math]O(n\cdot\log(maxX)\cdot\log(maxY))[/math] , а запросы выполняются за [math]O(\log (maxX)\cdot\log (maxY))[/math]
Добавляя точку вызовем [math]\mathrm(x, y, 1)[/math] , а удаляя [math]\mathrm(x, y, -1)[/math] . Таким образом запрос [math]\mathrm(x, y)[/math] дает количество точек в прямоугольнике.
Пример дерева Фенвика [math](16 \times 8)[/math] . Синим обозначены элементы, которые обновятся при изменении ячейки [math](5, 3)[/math] . Чтобы обновить элемент [math](X, Y)[/math] , по первой координате нам надо зайти во все столбцы(деревья по второй координате), находящиеся левее [math]X[/math] и на одной горизонтальной линии с ним, и в каждом из них обновить все ячейки под [math]Y[/math] (в рамках обозначений данного рисунка).
Псевдокод
[math]\mathtt[/math] — массив, в котором хранится дерево Фенвика.
int sum(x: int, y: int): int result = 0 for (int i = x; i >= 0; i = (i & (i + 1)) - 1) for (int j = y; j >= 0; j = (j & (j + 1)) - 1) result += t[i][j]; return result;
func inc(x: int, y: int, delta: int): for (int i = x; i < maxX; i = (i | (i + 1))) for (int j = y; j < maxY; j = (j | (j + 1))) t[i][j] += delta;
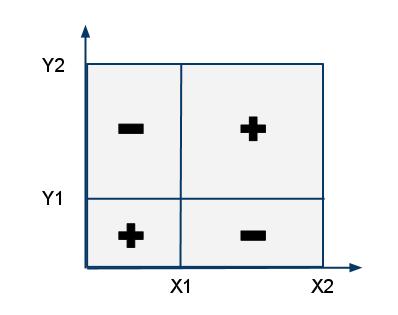
Чтобы посчитать значение функции для прямоугольника [math](x_1, y_1), (x_2, y_2)[/math] нужно воспользоваться формулой включения-исключения. Например, для суммы: [math]s = \mathrm(x_2,y_2)-\mathrm(x_2,y_1 - 1)-\mathrm(x_1 - 1,y_2)+\mathrm(x_1 - 1,y_1 - 1)[/math]
Обобщение на большие размерности
Дерево Фенвика относится к структурам данных, требующим малое количество дополнительной памяти. В комбинации с простым представлением тривиального случая данной структуры это дает возможность легко повышать размерность дерева Фенвика, в котором в ячейках какого-то фиксированного уровня будет находиться дерево меньшей размерности. Для его реализации нам достаточно во всех операциях для каждой новой размерности просто добавить вложенный цикл, пробегающий в ней соответствующие индексы.
См. также
Источники информации
Источник