Дерево графа корень дерева

Определение и свойства деревьев.

Деревом называется произвольный связный граф без циклов. Деревья обладают следующими свойствами:

любые две вершины соединены единственной простои цепью

количество ребер на единицу меньше количества вершин

при удалении любого ребра дерево становится не связным графом

при добавлении к дереву любого ребра в дереве появляется ровно один простой цикл.

Фактически дерево можно получить из любого связного графа

Утверждение: любой связный граф содержит остовный подграф который является деревом. Этот подграф называется остовыным деревом.

Специальные виды деревьев

1 Корневые деревья

Определение: Корневое дерево — ориентированное дерево, которое удовлетворяет условиям:

a) Имеется ровно один узел в который не входит не одно

В каждый узел кроме корня входит ровно одно ребро

Из корня имеется путь к любому ребру.

Если имеется путь от вершины vl к вершине v2, тогда вершина vl предок вершины v2, а вершина v2 потомок вершины vl.

Вершина которая не имеет потомков называется концевой вершиной или листом. Не концевую вершину называют внутренней. Если V₁ и V₂ дуга корневого дерева, то V₁— отец, a V₂— сын

Глубина дерева — длина пути из корня. Узлы находящиеся на одной глубине называются ярусами дерева.

Для задания корневого дерева можно использовать те же способы, что и для любого графа. На практике для представления деревьев используется канонический способ: для каждого узла хранится указатель на отца.

2 Бинарные деревья

Определение: Бинарное дерево — корневое дерево у каждой вершины которого не более двух сыновей.

В таком дереве любой произвольный узел имеет левого и правого сына. Поддерево корнем которого является левый сын называется левым поддеревом. Поддерево корнем которого является правый сын называется правым поддеревом.

Имеется два способа представления бинарных деревьев:

1. Представление в виде двух массивов: первый массив- левые сыновья, второй — правые.

2. Представление в виде списковой структуры tree_ ptr Tree_mode — запись имеющая структуру:

Element- тип узла; Left: tree_ ptr; Right: tree_ ptr;

3 Полные бинарные деревья

Определение: Полное бинарное дерево — бинарное дерево для которого выполняются условия:

a) Заполнение дерева осуществляется от корня к листьям по уровням.

b) Заполнение уровней осуществляется слева направо.

Полные бинарные деревья представляются в виде одномерного массива: первый элемент массива — корень дерева. Для любого i-того узла элемент с индексом (2i) — левый сын, элемент с индексом (2i+l)- правый сын. Отец узла j — (j/2).

4 Бинарные поисковые деревья

Определение: Бинарное поисковое дерево — дерево поиска,

Все ключи в левом поддереве меньше ключа узла V

В правом поддереве все ключи больше, чем ключ V

В дереве нет одинаковых ключей.

5 Сбалансированные деревья

Определение: Дерево называется идеально сбалансированным, если оно является бинарным поисковым деревом и число вершин его левых и правых поддеревьев отличается не более, чем на единицу.

Определение: Дерево называется сбалансированным, если оно бинарное поисковое и высоты двух поддеревьев в каждой из вершин отличаются не более, чем на единицу.

6 Способы обхода узлов в бинарных деревьях

Большинство алгоритмов при работе с деревьями посещают каждый узел в некотором порядке.

Существует три наиболее распространенных способа обхода деревьев:

1. Прямой порядок: корень посещается раньше, чем поддеревья

Порядок обхода: корень — левое поддерево — правое поддерево.

Процедура организуется рекурсивно.

2. Обратный порядок (снизу вверх): корень посещается после поддеревьев.

Порядок обхода: левое поддерево — правое поддерево- корень.

3. Внутренний порядок (слева направо )

Порядок обхода: левое поддерево – корень — правое поддерево.

7 Представление множеств с помощью деревьев

Базовыми операциями над множествами являются:

определение принадлежности элемента множества.

объединение не пересекающихся множеств.

Каждое множество будем представлять в виде корневого дерева. Корень дерева можно использовать для хранения имени множества. Дерево будем представлять в каноническом виде.

Чтобы определить, к какому множеству принадлежит некоторый элемент — находим этот элемент и определяем корень множества, к которому он принадлежит. Этот корень — есть имя искомого множества.

Объединение непересекающихся множеств можем реали­зовать тремя способами:

Источник

Лекция № 14. Деревья

1. Основные определения

Дерево – связный граф без циклов. Лес (или ациклический граф) – неограф без циклов. Компонентами леса являются деревья. Теорема 14.1.Для неографаGсnвершинами без петель следующие условия эквивалентны:

1. G– дерево;
2. G– связной граф, содержащийn– 1 ребро;
3. G– ациклический граф, содержащийn– 1 ребро;
4. Любые две несовпадающие вершины графаGсоединяет единственная цепь;
5. G– ациклический граф, такой, что если в него добавить одно ребро, то в нем появится ровно один цикл.

Теорема 14.2.НеографGявляется лесом тогда и только тогда, когда коранг графаv(G)=0. Висячая вершина в дереве – вершина степени 1. Висячие вершины называются листьями, все остальные – внутреннимивершинами. Если в дереве особо выделена одна вершина, называемая корнем, то такое дерево называется корневым, иначе – свободным. Корневое дерево можно считать орграфом с ориентацией дуг из корня или в корень. Очевидно, что для любой вершины корневого дерева, кроме корня, . Для корня, для листьев. Вершины дерева, удаленные на расстояние k (в числе дуг) от корня, образуют k-й ярус (уровень) дерева. Наибольшее значение k называется высотой дерева. Если из какой-либо вершины корневого дерева выходят дуги, то вершины на концах этих дуг называют сыновьями (в английской литературе – дочери (daughter)).

1. Центроид дерева

Ветвь к вершине v дерева – это максимальный подграф, содержащий v в качестве висячей вершины. Вес вершиныk – наибольший размер ее ветвей. Центроид (или центр масс) дерева C – множество вершин с наименьшим весом: C = v| c(v) = >. Вес любого листа дерева равен размеру дерева. Высота дерева с корнем, расположенным в центроиде, не больше наименьшего веса его вершин. Свободное дерево порядка n с двумя центроидами имеет четное количество вершин, а вес каждого центроида равен n/2. Теорема 14.3 (Жордана).Каждое дерево имеет центроид, состоящий из одной или двух смежных вершин.Пример 14.1. Найти наименьший вес вершин дерева, изображенного на рис. 14.1, и его центроид. Рис. 14.1 Решение. Очевидно, что вес каждой висячей вершины дерева порядка n равен n – 1. Висячие вершины не могут составить центроид дерева, поэтому исключим из рассмотрения вершины 1, 2, 4, 6, 12, 13 и 16. Для всех остальных вершин найдем их вес, вычисляя длину (размер) их ветвей. Число ветвей вершины равно ее степени. Вершины 3, 5 и 8 имеют по две ветви, размеры которых равны 1 и 14. К вершине 7 подходят четыре ветви размером 1, 2, 2 и 10. Таким образом, ее вес . Аналогично вычисляются веса других вершин:,,. Минимальный вес вершин равен 8, следовательно, центроид дерева образуют две вершины с таким весом: 11 и 15.

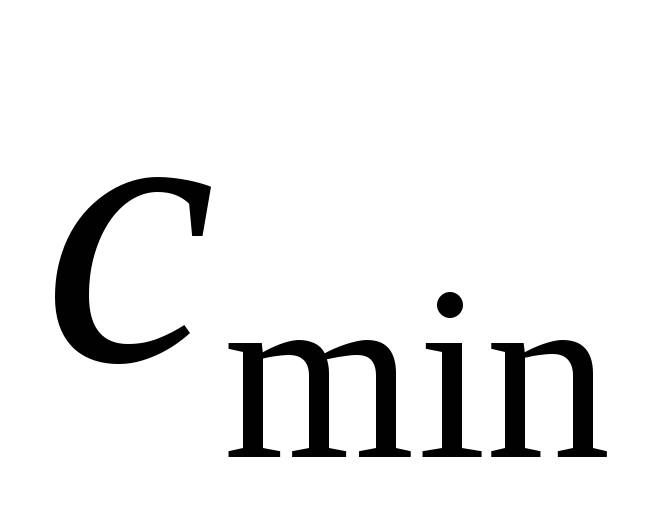
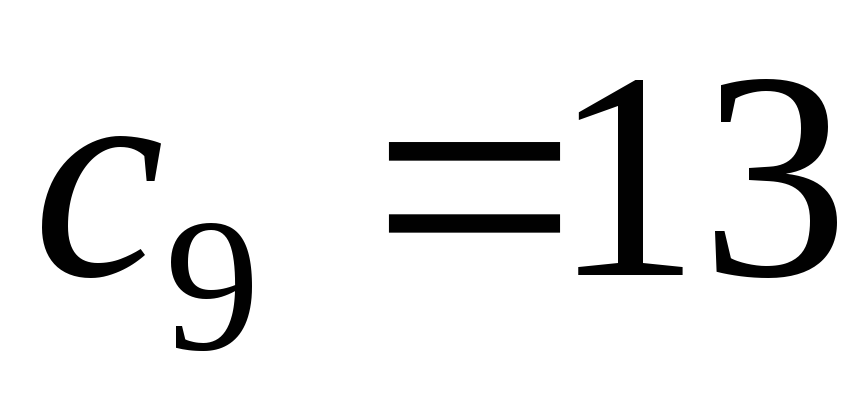
1. Десятичная кодировка

Деревья представляют собой важный вид графов. С помощью деревьев описываются базы данных, деревья моделируют алгоритмы и программы, их используют в электротехнике, химии. Одной из актуальных задач в эпоху компьютерных и телекоммуникационных сетей является задача сжатия информации. Сюда входит и кодировка деревьев. Компактная запись дерева, полностью описывающая его структуру, может существенно упростить как передачу информации о дереве, так и работу с ним. Существует множество способов кодировки деревьев. Рассмотрим одну из простейших кодировок помеченных деревьев с выделенным корнем – десятичную. Кодируя дерево, придерживаемся следующих правил.

1. Кодировка начинается с корня и заканчивается в корне.
2. Каждый шаг на одну дугу от корня кодируется единицей.
3. В узле выбираем направление на вершину с меньшим номером.
4. Достигнув листа, идем назад, кодируя каждый шаг нулем.
5. При движении назад в узле всегда выбираем направление на непройденную вершину с меньшим номером.

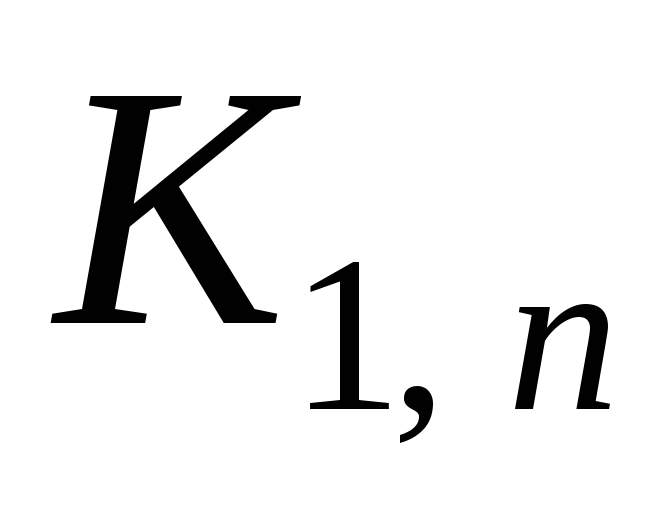
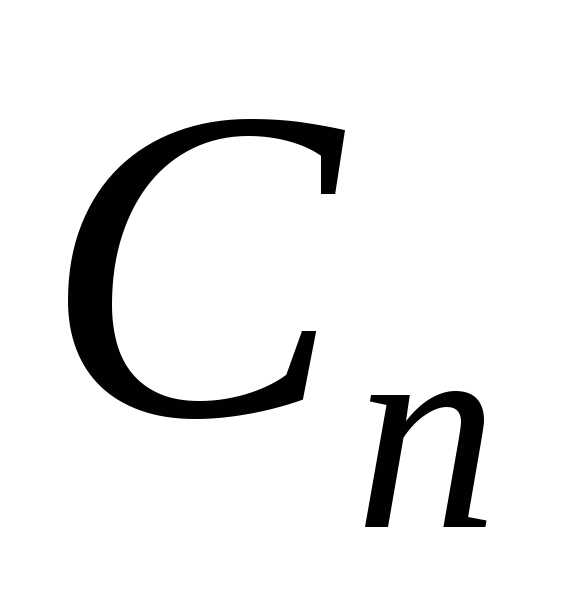
Кодировка в такой форме получается достаточно компактной, однако она не несет в себе информации о номерах вершин дерева. Существуют аналогичные кодировки, где вместо единиц в таком же порядке проставляются номера или названия вершин. Есть деревья, для которых несложно вывести формулу десятичной кодировки. Рассмотрим, например, графы-звезды , являющиеся полными двудольными графами, одна из долей которых состоит из одной вершины. Другое обозначение звезд –. На рис. 14.2 показаны звезды, а также приведены их двоичные и десятичные кодировки. Корень дерева располагается в центральной вершине звезды. Легко получить общую формулу: . (14.1) Рис. 14.2 Если корень поместить в любой из висячих вершин, то код такого дерева будет выражаться большим числом. Более того, существует зависимость. Аналогично рассматриваются и цепи (рис. 14.3). Цепи обозначаются как. Рис. 14.3 В звездах только два варианта расположения корня с различными десятичными кодировками. В цепи же число вариантов кодировок в зависимости от положения корня растет с увеличением n. Рассмотрим самый простой вариант, расположив корень в концевой вершине (листе). Для получим двоичную кодировку 10 и десятичную 2, для– 1100 и 12, для– 111000 и 56, для– 11110000 и 240. Общая формула для десятичной кодировки цепи с корнем в концевой вершине имеет вид . (14.2) Пример 14.2. Записать десятичный код дерева, изображенного на рис. 14.4, с корнем в вершине 3. Рис. 14.4 Решение. На основании правила кодировки, двигаясь по дереву, проставим в код единицы и нули. При движении из корня 3 к вершине 7 проходим четыре ребра. В код записываем четыре единицы: 1111. Возвращаясь от вершины 7 к вершине 2 (до ближайшей развилки), проходим три ребра. Записываем в код три нуля: 000. От вершины 2 к 5 и далее к 8 (меньший номер): 11; от 8 назад к 5 и от 5 к 9: 01; от 9 к корню 3: 000. И, наконец, от 3 к 6 и обратно: 10. В итоге, собирая все вместе, получим двоичный код дерева: 1 111 000 110 100 010. Разбивая число на тройки, переводим полученное двоичное представление в восьмеричное. Получаем . Затем переводим это число в десятичное:.

Для продолжения скачивания необходимо пройти капчу:

Источник