Алгоритм Хаффмана на пальцах
Вы вероятно слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то поищите информацию в интернете — в этой статье я не буду вас грузить историей или математикой. Сегодня я хочу просто попытаться показать вам практический пример применения алгоритма к символьной строке.
Примечание переводчика: под символом автор подразумевает некий повторяющийся элемент исходной строки — это может быть как печатный знак (character), так и любая битовая последовательность. Под кодом подразумевается не ASCII или UTF-8 код символа, а кодирующая последовательность битов.
К статье прикреплён исходный код, который наглядно демонстрирует, как работает алгоритм Хаффмана — он предназначен для людей, которые плохо понимают математику процесса. В будущем (я надеюсь) я напишу статью, в которой мы поговорим о применении алгоритма к любым файлам для их сжатия (то есть, сделаем простой архиватор типа WinRAR или WinZIP).
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). Для нашей программы я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Мы могли бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами. В исходном коде я использовал код очереди с приоритетами из моей предыдущей статьи.
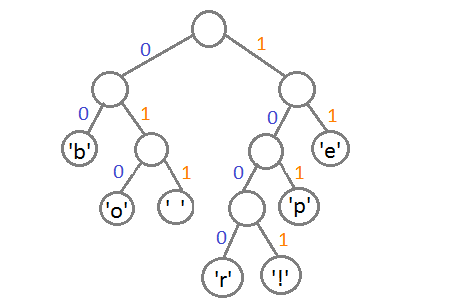
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит (на практике, в нашей программе мы выведем на консоль последовательность из 40 нулей и единиц, представляющих собой биты кодированного текста. Чтобы получить из них настоящую строку размером 40 бит, нужно применять битовую арифметику, поэтому мы сегодня не будем этого делать).
Чтобы лучше понять пример, мы для начала сделаем всё вручную. Строка «beep boop beer!» для этого очень хорошо подойдёт. Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов:
| Символ | Частота |
|---|---|
| ‘b’ | 3 |
| ‘e’ | 4 |
| ‘p’ | 2 |
| ‘ ‘ | 2 |
| ‘o’ | 2 |
| ‘r’ | 1 |
| ‘!’ | 1 |
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь. 
Повторим те же шаги и получим последовательно: 
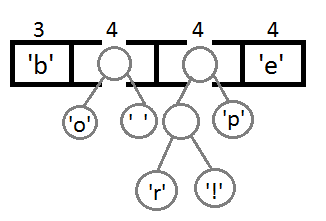
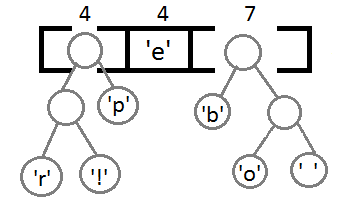
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
| Символ | Код |
|---|---|
| ‘b’ | 00 |
| ‘e’ | 11 |
| ‘p’ | 101 |
| ‘ ‘ | 011 |
| ‘o’ | 010 |
| ‘r’ | 1000 |
| ‘!’ | 1001 |
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для ‘b’, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на ‘b’.
На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: «beep boop beer!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.
Приложенный исходный код работает по тому же принципу, что и описан выше. В коде можно найти больше деталей и комментариев.
Все исходники были откомпилированы и проверены с использованием стандарта C99. Удачного программирования!
Чтобы прояснить ситуацию: данная статья только иллюстрирует работу алгоритма. Чтобы использовать это в реальной жизни, вам надо будет поместить созданное вами дерево Хаффмана в закодированную строку, а получатель должен будет знать, как его интерпретировать, чтобы раскодировать сообщение. Хорошим способом сделать это, является проход по дереву в любом порядке, который вам нравится (я предпочитаю обход в глубину) и конкатенировать 0 для каждого узла и 1 для листа с битами, представляющими оригинальный символ (в нашем случае, 8 бит, представляющие ASCII-код знака). Идеальным было бы добавить это представление в самое начало закодированной строки. Как только получатель построит дерево, он будет знать, как декодировать сообщение, чтобы прочесть оригинал.
Источник
Алгоритм сжатия кода Хаффмана
Кодирование Хаффмана (также известное как кодирование Хаффмана) — это алгоритм сжатия данных, который формирует основную идею сжатия файлов. В этом посте рассказывается о кодировании с фиксированной и переменной длиной, уникально декодируемых кодах, правилах префиксов и построении дерева Хаффмана.
Обзор
Мы уже знаем, что каждый символ представляет собой последовательность 0’s а также 1’s и хранится с использованием 8-бит. Это известно как “кодирование с фиксированной длиной”, так как каждый символ использует одинаковое количество фиксированных битов памяти.
Учитывая текст, как уменьшить количество места, необходимое для хранения символа?
Идея состоит в том, чтобы использовать “кодирование переменной длины”. Мы можем использовать тот факт, что одни символы встречаются в тексте чаще, чем другие (см. это) для разработки алгоритма, который может представлять тот же фрагмент текста, используя меньшее количество битов. При кодировании с переменной длиной мы присваиваем символам переменное количество битов в зависимости от их частоты в данном тексте. Таким образом, некоторые символы могут в конечном итоге занимать один бит, а некоторые — два бита, некоторые могут быть закодированы с использованием трех битов и так далее. Проблема с кодированием переменной длины заключается в его декодировании.
Учитывая последовательность битов, как ее однозначно декодировать?
Рассмотрим строку aabacdab . Оно имеет 8 символов в нем и использует 64-битное хранилище (с использованием кодирования фиксированной длины). Если принять во внимание, что частота символов a , b , c а также d находятся 4 , 2 , 1 , 1 , соответственно. Попробуем представить aabacdab используя меньшее количество битов, используя тот факт, что a встречается чаще, чем b , а также b встречается чаще, чем c а также d . Начнем со случайного присвоения однобитового кода 0 к a , 2-битный код 11 к b , и 3-битный код 100 а также 011 к персонажам c а также d , соответственно.
Итак, строка aabacdab будет закодирован в 00110100011011 (0|0|11|0|100|011|0|11) используя приведенные выше коды. Но настоящая проблема заключается в расшифровке. Если мы попытаемся декодировать строку 00110100011011 , это приведет к неоднозначности, так как его можно декодировать,
0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
…
and so on
Чтобы предотвратить двусмысленность при декодировании, мы обеспечим соответствие нашего кодирования “правилу префикса”, что приведет к “уникально декодируемым кодам”. Правило префикса гласит, что ни один код не является префиксом другого кода. Под кодом мы подразумеваем биты, используемые для определенного символа. В приведенном выше примере 0 является префиксом 011 , что нарушает правило префикса. Если наши коды удовлетворяют префиксному правилу, декодирование будет однозначным (и наоборот).
Давайте снова рассмотрим приведенный выше пример. На этот раз мы присваиваем символам коды, удовлетворяющие правилу префикса. ‘a’ , ‘b’ , ‘c’ , а также ‘d’ .
Используя приведенные выше коды, строка aabacdab будет закодирован в 00100110111010 (0|0|10|0|110|111|0|10) . Теперь мы можем однозначно декодировать 00100110111010 вернуться к нашей исходной строке aabacdab .
Теперь, когда мы разобрались с кодированием переменной длины и правилом префиксов, давайте поговорим о кодировании Хаффмана.
Кодирование Хаффмана
Техника работает, создавая бинарное дерево узлов. Узел может быть листовым узлом или внутренним узлом. Изначально все узлы являются листовыми узлами, которые содержат сам персонаж, вес (частоту появления) персонажа. Внутренние узлы содержат вес символов и ссылки на два дочерних узла. По общему соглашению, бит 0 представляет следующий левый дочерний элемент, и немного 1 представляет следующий правильный ребенок. Готовое дерево имеет n листовые узлы и n-1 внутренние узлы. Рекомендуется, чтобы дерево Хаффмана отбрасывало неиспользуемые символы в тексте, чтобы получить наиболее оптимальную длину кода.
Мы будем использовать приоритетная очередь для построения дерева Хаффмана, где узел с наименьшей частотой имеет наивысший приоритет. Ниже приведены полные шаги:
1. Создайте конечный узел для каждого символа и добавьте их в очередь приоритетов.
2. Пока в queue больше одного узла:
- Удалите из queue два узла с наивысшим приоритетом (самой низкой частотой).
- Создайте новый внутренний узел с этими двумя узлами в качестве дочерних элементов и частотой, равной сумме частот обоих узлов.
- Добавьте новый узел в очередь приоритетов.
3. Оставшийся узел является корневым узлом, и дерево завершено.
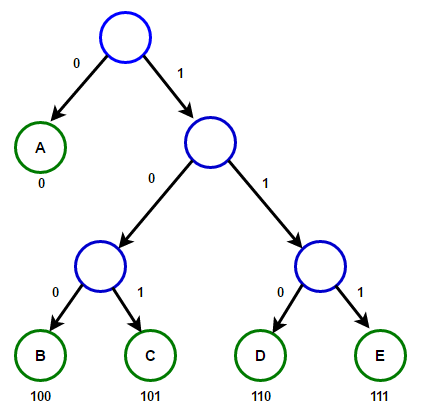
Рассмотрим некоторый текст, состоящий только из ‘A’ , ‘B’ , ‘C’ , ‘D’ , а также ‘E’ символов, а их частота 15 , 7 , 6 , 6 , 5 , соответственно. Следующие рисунки иллюстрируют шаги, за которыми следует алгоритм:
Путь от корня к любому конечному узлу хранит оптимальный код префикса (также называемый кодом Хаффмана), соответствующий символу, связанному с этим конечным узлом.
Реализация
Ниже приведена реализация алгоритма сжатия кода Хаффмана на C++, Java и Python:
Источник