Алгоритм Хаффмана на пальцах
Вы вероятно слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то поищите информацию в интернете — в этой статье я не буду вас грузить историей или математикой. Сегодня я хочу просто попытаться показать вам практический пример применения алгоритма к символьной строке.
Примечание переводчика: под символом автор подразумевает некий повторяющийся элемент исходной строки — это может быть как печатный знак (character), так и любая битовая последовательность. Под кодом подразумевается не ASCII или UTF-8 код символа, а кодирующая последовательность битов.
К статье прикреплён исходный код, который наглядно демонстрирует, как работает алгоритм Хаффмана — он предназначен для людей, которые плохо понимают математику процесса. В будущем (я надеюсь) я напишу статью, в которой мы поговорим о применении алгоритма к любым файлам для их сжатия (то есть, сделаем простой архиватор типа WinRAR или WinZIP).
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). Для нашей программы я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Мы могли бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами. В исходном коде я использовал код очереди с приоритетами из моей предыдущей статьи.
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит (на практике, в нашей программе мы выведем на консоль последовательность из 40 нулей и единиц, представляющих собой биты кодированного текста. Чтобы получить из них настоящую строку размером 40 бит, нужно применять битовую арифметику, поэтому мы сегодня не будем этого делать).
Чтобы лучше понять пример, мы для начала сделаем всё вручную. Строка «beep boop beer!» для этого очень хорошо подойдёт. Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов:
| Символ | Частота |
|---|---|
| ‘b’ | 3 |
| ‘e’ | 4 |
| ‘p’ | 2 |
| ‘ ‘ | 2 |
| ‘o’ | 2 |
| ‘r’ | 1 |
| ‘!’ | 1 |
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
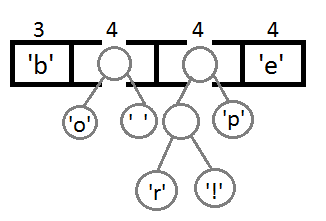
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь. 
Повторим те же шаги и получим последовательно: 
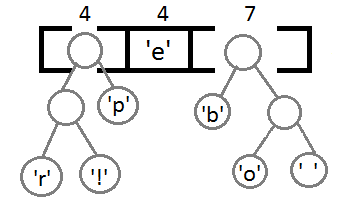
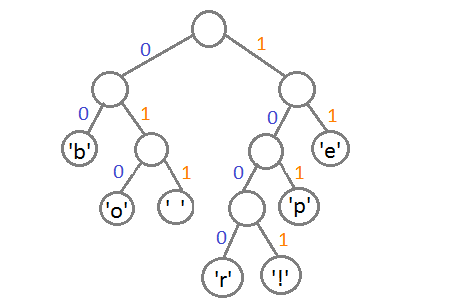
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
| Символ | Код |
|---|---|
| ‘b’ | 00 |
| ‘e’ | 11 |
| ‘p’ | 101 |
| ‘ ‘ | 011 |
| ‘o’ | 010 |
| ‘r’ | 1000 |
| ‘!’ | 1001 |
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для ‘b’, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на ‘b’.
На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: «beep boop beer!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.
Приложенный исходный код работает по тому же принципу, что и описан выше. В коде можно найти больше деталей и комментариев.
Все исходники были откомпилированы и проверены с использованием стандарта C99. Удачного программирования!
Чтобы прояснить ситуацию: данная статья только иллюстрирует работу алгоритма. Чтобы использовать это в реальной жизни, вам надо будет поместить созданное вами дерево Хаффмана в закодированную строку, а получатель должен будет знать, как его интерпретировать, чтобы раскодировать сообщение. Хорошим способом сделать это, является проход по дереву в любом порядке, который вам нравится (я предпочитаю обход в глубину) и конкатенировать 0 для каждого узла и 1 для листа с битами, представляющими оригинальный символ (в нашем случае, 8 бит, представляющие ASCII-код знака). Идеальным было бы добавить это представление в самое начало закодированной строки. Как только получатель построит дерево, он будет знать, как декодировать сообщение, чтобы прочесть оригинал.
Источник
Алгоритм Хаффмана
Слабое место метода упаковки заключается в том, что символы кодируются битовыми последовательностями одинаковой длины. Например, любой текст, состоящий только из двух букв «А» и «В», сжимается методом упаковки в восемь раз. Однако если к такому тексту добавить всего лишь одну букву, например «С», то степень сжатия сразу уменьшится вдвое, причем независимо от длины текста и количества добавленных символов «С»!
Улучшения степени сжатия можно достичь, кодируя часто встречающиеся символы короткими кодами, а редко встречающиеся — более длинными. Именно такова идея метода, опубликованного Д. Хаффманом (Huffman) в 1952 г.
Идея кодирования символов кодами переменной длины была высказана и теоретически проработана американскими учеными К. Шенноном и Р. М. Фано. Ими был предложен алгоритм построения эффективных сжимающих кодов переменной длины (алгоритм Шеннона—Фано), однако он в некоторых случаях строил неоптимальные коды. Алгоритм Хаффмана оказался простым, быстрым и оптимальным: среди алгоритмов, кодирующих каждый символ по отдельности и целым количеством бит, он обеспечивает наилучшее сжатие.
Алгоритм Хаффмана сжимает данные за два прохода: на первом проходе читаются все входные данные и подсчитываются частоты встречаемости всех символов. Затем по этим данным строится дерево кодирования Хаффмана, а по нему — коды символов. После этого, на втором проходе, входные данные читаются еще раз и при этом генерируется выходной массив данных.
Вычисление частот встречаемости — тривиальная задача. Разберем построение дерева кодирования Хаффмана.
Алгоритм построения дерева Хаффмана
- Символы входного алфавита образуют список свободных узлов. Каждый узел имеет вес, равный количеству вхождений символа в исходное сообщение.
- В списке выбираются два свободных узла с наименьшими весами
- Создается их узел-«родитель» с весом, равным сумме их весов, он соединяется с «детьми» дугами.
- Одной дуге, выходящей из «родителя», ставится в соответствие бит 1, другой — бит 0.
- «Родитель» добавляется в список свободных узлов, а двое его «детей» удаляются из этого списка.
- Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева
Пример. Построение дерева Хаффмана и префиксных кодов для текста «KOJI_OKOJIO_KOJIOKOJIA»:
Пусть у нас имеется список частот встречаемости всех символов исходного текста. Выпишем их вертикально в ряд в виде вершин будущего графа. Выберем две вершины с наименьшими весами (они соответствуют символам с наименьшим количеством повторений). Объединим эти вершины — создадим новую вершину, от которой проведем ребра к выбранным вершинам с наименьшими весами, а вес новой вершины зададим равным сумме их весов. Расставим на ребрах графа числа 0 и 1, например на каждом верхнем ребре 0, а на каждом нижнем — 1. Чтобы выбранные вершины более не просматривались, мы сотрем их веса (это аналог удаления вершин из списка). Продолжим выполнять объединение вершин, каждый раз выбирая пару вершин с наименьшими весами, до тех пор пока не останется одна вершина. Очевидно, что вес этой вершины будет равен длине сжимаемого массива данных.
Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до этой буквы, выписывая нули и единицы по маршруту следования. В нашем примере символы получат следующие коды:
«О» — 00, «К» — 01 «Л» — 10 «_» — 110 «А» — 111
После того как коды символов построены, остается сгенерировать сжатый массив данных, для чего надо снова прочесть входные данные и каждый символ заменить на соответствующий код. В нашем случае непосредственно код текста будет занимать 39 бит, или 5 байт. Коэффициент сжатия равен 18/5 = 3,6. Для восстановления сжатых данных необходимо снова воспользоваться деревом Хаффмана, так как код каждого символа представляет собой путь в дереве Хаффмана от вершины до конечного узда дерева, соответствующего данному символу. Общая схема процесса восстановления такова: специальный маркер устанавливается в вершину дерева Хаффмана, и сжатый массив данных читается побитово. Если читаемый бит равен О, то маркер перемещается из вершины по верхнему ребру, если 1, то по нижнему. Затем читается следующий бит, и маркер снова перемещается, и т. д., пока маркер не попадет в один из конечных узлов дерева. В восстанавливаемый массив записывается символ, которому соответствует этот конечный узел, маркер снова помещается в вершину дерева, и процесс повторяется.
Код Хаффмана является префиксным. Это означает, что код каждого символа не является началом кода какого-либо другого символа. Код Хаффмана однозначно восстановим, даже если не сообщается длина кода каждого переданного символа.
Источник