Дерево хаффмана пример построения

Алгоритм Хаффмана

Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.

Определение

• [math]c_[/math] не является префиксом для [math]c_[/math] , при [math]i \ne j[/math] ,

• cумма [math]\sum\limits_ w_\cdot |c_|[/math] минимальна ( [math]|c_|[/math] — длина кода [math]c_[/math] ),

Алгоритм построения бинарного кода Хаффмана

Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:

1. Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
2. Из списка выберем два узла с наименьшим весом.
3. Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
4. Добавим к списку только что сформированный узел вместо двух объединенных узлов.
5. Если в списке больше одного узла, то повторим пункты со второго по пятый.

Время работы

Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время [math]O(N \log N)[/math] .Такую асимптотику можно улучшить до [math]O(N)[/math] , используя обычные массивы.

Пример

Закодируем слово [math]abracadabra[/math] . Тогда алфавит будет [math]A= \ [/math] , а набор весов (частота появления символов алфавита в кодируемом слове) [math]W=\[/math] :

В дереве Хаффмана будет [math]5[/math] узлов:

Узел	a	b	r	с	d
Вес	5	2	2	1	1

По алгоритму возьмем два символа с наименьшей частотой — это [math]c[/math] и [math]d[/math] . Сформируем из них новый узел [math]cd[/math] весом [math]2[/math] и добавим его к списку узлов:

Узел	a	b	r	cd
Вес	5	2	2	2

Затем опять объединим в один узел два минимальных по весу узла — [math]r[/math] и [math]cd[/math] :

Еще раз повторим эту же операцию, но для узлов [math]rcd[/math] и [math]b[/math] :

На последнем шаге объединим два узла — [math]brcd[/math] и [math]a[/math] :

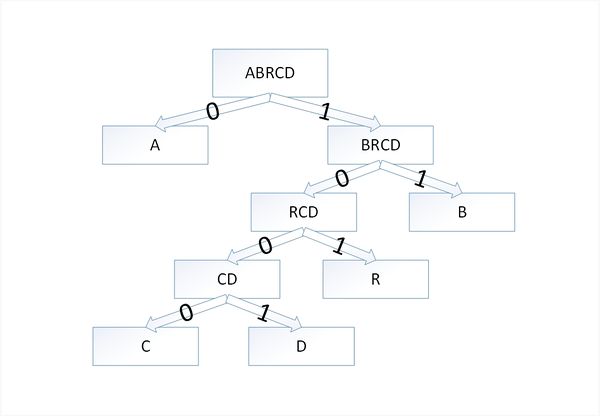
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):

Символ	a	b	r	с	d
Код	0	11	101	1000	1001

Таким образом, закодированное слово [math]abracadabra[/math] будет выглядеть как [math]01110101000010010111010[/math] . Длина закодированного слова — [math]23[/math] бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы [math]33[/math] бита, что существенно больше.

Корректность алгоритма Хаффмана

Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.

Пусть [math]C[/math] — алфавит, каждый символ [math]c \in C[/math] которого встречается с частотой [math]f[c][/math] . Пусть [math]x[/math] и [math]y[/math] — два символа алфавита [math]C[/math] с самыми низкими частотами. Тогда для алфавита [math]C[/math] существует оптимальный префиксный код, кодовые слова символов [math]x[/math] и [math]y[/math] в котором имеют одинаковую максимальную длину и отличаются лишь последним битом.

Возьмем дерево [math]T[/math] , представляющее произвольный оптимальный префиксный код для алфавита [math]C[/math] . Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] — листья с общим родительским узлом, находящиеся на максимальной глубине.

Пусть символы [math]a[/math] и [math]b[/math] имеют общий родительский узел и находятся на максимальной глубине дерева [math]T[/math] . Предположим, что [math]f[a] \leqslant f[b][/math] и [math]f[x] \leqslant f[y][/math] . Так как [math]f[x][/math] и [math]f[y][/math] — две наименьшие частоты, а [math]f[a][/math] и [math]f[b][/math] — две произвольные частоты, то выполняются отношения [math]f[x] \leqslant f[a][/math] и [math]f[y] \leqslant f[b][/math] . Пусть дерево [math]T'[/math] — дерево, полученное из [math]T[/math] путем перестановки листьев [math]a[/math] и [math]x[/math] , а дерево [math]T»[/math] — дерево полученное из [math]T'[/math] перестановкой листьев [math]b[/math] и [math]y[/math] . Разность стоимостей деревьев [math]T[/math] и [math]T'[/math] равна:

[math]B(T) — B(T’) = \sum\limits_ f(c)d_T(c) — \sum\limits_ f(c)d_(c) = (f[a] — f[x])(d_T(a) — d_T(x)),[/math]

что больше либо равно [math]0[/math] , так как величины [math]f[a] — f[x][/math] и [math]d_T(a) — d_T(x)[/math] неотрицательны. Величина [math]f[a] — f[x][/math] неотрицательна, потому что [math]x[/math] — лист с минимальной частотой, а величина [math]d_T(a) — d_T(x)[/math] является неотрицательной, так как лист [math]a[/math] находится на максимальной глубине в дереве [math]T[/math] . Точно так же перестановка листьев [math]y[/math] и [math]b[/math] не будет приводить к увеличению стоимости. Таким образом, разность [math]B(T’) — B(T»)[/math] тоже будет неотрицательной.

Пусть дан алфавит [math]C[/math] , в котором для каждого символа [math]c \in C[/math] определены частоты [math]f[c][/math] . Пусть [math]x[/math] и [math]y[/math] — два символа из алфавита [math]C[/math] с минимальными частотами. Пусть [math]C'[/math] — алфавит, полученный из алфавита [math]C[/math] путем удаления символов [math]x[/math] и [math]y[/math] и добавления нового символа [math]z[/math] , так что [math]C’ = C \backslash \ < x, y \>\cup [/math] . По определению частоты [math]f[/math] в алфавите [math]C'[/math] совпадают с частотами в алфавите [math]C[/math] , за исключением частоты [math]f[z] = f[x] + f[y][/math] . Пусть [math]T'[/math] — произвольное дерево, представляющее оптимальный префиксный код для алфавита [math]C'[/math] Тогда дерево [math]T[/math] , полученное из дерева [math]T'[/math] путем замены листа [math]z[/math] внутренним узлом с дочерними элементами [math]x[/math] и [math]y[/math] , представляет оптимальный префиксный код для алфавита [math]C[/math] .

Сначала покажем, что стоимость [math]B(T)[/math] дерева [math]T[/math] может быть выражена через стоимость [math]B(T’)[/math] дерева [math]T'[/math] . Для каждого символа [math]c \in C \backslash \[/math] верно [math]d_T(C) = d_[/math] , значит, [math]f[c]d_T(c) = f[c]d_(c)[/math] . Так как [math]d_T(x) = d_T(y) = d_ (z) + 1[/math] , то

[math]f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_(z) + 1) = f[z]d_(z) + (f[x] + f[y])[/math]

Докажем лемму от противного. Предположим, что дерево [math]T[/math] не представляет оптимальный префиксный код для алфавита [math]C[/math] . Тогда существует дерево [math]T»[/math] такое, что [math]B(T») \lt B(T)[/math] . Согласно лемме (1), элементы [math]x[/math] и [math]y[/math] можно считать дочерними элементами одного узла. Пусть дерево [math]T»'[/math] получено из дерева [math]T»[/math] заменой элементов [math]x[/math] и [math]y[/math] листом [math]z[/math] с частотой [math]f[z] = f[x] + f[y][/math] . Тогда

[math]B(T»’) = B(T») — f[x] — f[y] \lt B(T) — f[x] — f[y] = B(T’)[/math] ,

См. также

Источники информации

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
• Wikipedia — Huffman coding
• Википедия — Бинарное дерево
• Википедия — Префиксный код

Источник

Алгоритм сжатия кода Хаффмана

Кодирование Хаффмана (также известное как кодирование Хаффмана) — это алгоритм сжатия данных, который формирует основную идею сжатия файлов. В этом посте рассказывается о кодировании с фиксированной и переменной длиной, уникально декодируемых кодах, правилах префиксов и построении дерева Хаффмана.

Обзор

Мы уже знаем, что каждый символ представляет собой последовательность 0’s а также 1’s и хранится с использованием 8-бит. Это известно как “кодирование с фиксированной длиной”, так как каждый символ использует одинаковое количество фиксированных битов памяти.

Учитывая текст, как уменьшить количество места, необходимое для хранения символа?

Идея состоит в том, чтобы использовать “кодирование переменной длины”. Мы можем использовать тот факт, что одни символы встречаются в тексте чаще, чем другие (см. это) для разработки алгоритма, который может представлять тот же фрагмент текста, используя меньшее количество битов. При кодировании с переменной длиной мы присваиваем символам переменное количество битов в зависимости от их частоты в данном тексте. Таким образом, некоторые символы могут в конечном итоге занимать один бит, а некоторые — два бита, некоторые могут быть закодированы с использованием трех битов и так далее. Проблема с кодированием переменной длины заключается в его декодировании.

Учитывая последовательность битов, как ее однозначно декодировать?

Рассмотрим строку aabacdab . Оно имеет 8 символов в нем и использует 64-битное хранилище (с использованием кодирования фиксированной длины). Если принять во внимание, что частота символов a , b , c а также d находятся 4 , 2 , 1 , 1 , соответственно. Попробуем представить aabacdab используя меньшее количество битов, используя тот факт, что a встречается чаще, чем b , а также b встречается чаще, чем c а также d . Начнем со случайного присвоения однобитового кода 0 к a , 2-битный код 11 к b , и 3-битный код 100 а также 011 к персонажам c а также d , соответственно.

Итак, строка aabacdab будет закодирован в 00110100011011 (0|0|11|0|100|011|0|11) используя приведенные выше коды. Но настоящая проблема заключается в расшифровке. Если мы попытаемся декодировать строку 00110100011011 , это приведет к неоднозначности, так как его можно декодировать,

0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
…
and so on

Чтобы предотвратить двусмысленность при декодировании, мы обеспечим соответствие нашего кодирования “правилу префикса”, что приведет к “уникально декодируемым кодам”. Правило префикса гласит, что ни один код не является префиксом другого кода. Под кодом мы подразумеваем биты, используемые для определенного символа. В приведенном выше примере 0 является префиксом 011 , что нарушает правило префикса. Если наши коды удовлетворяют префиксному правилу, декодирование будет однозначным (и наоборот).

Давайте снова рассмотрим приведенный выше пример. На этот раз мы присваиваем символам коды, удовлетворяющие правилу префикса. ‘a’ , ‘b’ , ‘c’ , а также ‘d’ .

Используя приведенные выше коды, строка aabacdab будет закодирован в 00100110111010 (0|0|10|0|110|111|0|10) . Теперь мы можем однозначно декодировать 00100110111010 вернуться к нашей исходной строке aabacdab .

Теперь, когда мы разобрались с кодированием переменной длины и правилом префиксов, давайте поговорим о кодировании Хаффмана.

Кодирование Хаффмана

Техника работает, создавая бинарное дерево узлов. Узел может быть листовым узлом или внутренним узлом. Изначально все узлы являются листовыми узлами, которые содержат сам персонаж, вес (частоту появления) персонажа. Внутренние узлы содержат вес символов и ссылки на два дочерних узла. По общему соглашению, бит 0 представляет следующий левый дочерний элемент, и немного 1 представляет следующий правильный ребенок. Готовое дерево имеет n листовые узлы и n-1 внутренние узлы. Рекомендуется, чтобы дерево Хаффмана отбрасывало неиспользуемые символы в тексте, чтобы получить наиболее оптимальную длину кода.

Мы будем использовать приоритетная очередь для построения дерева Хаффмана, где узел с наименьшей частотой имеет наивысший приоритет. Ниже приведены полные шаги:

1. Создайте конечный узел для каждого символа и добавьте их в очередь приоритетов.

2. Пока в queue больше одного узла:

• Удалите из queue два узла с наивысшим приоритетом (самой низкой частотой).
• Создайте новый внутренний узел с этими двумя узлами в качестве дочерних элементов и частотой, равной сумме частот обоих узлов.
• Добавьте новый узел в очередь приоритетов.

3. Оставшийся узел является корневым узлом, и дерево завершено.

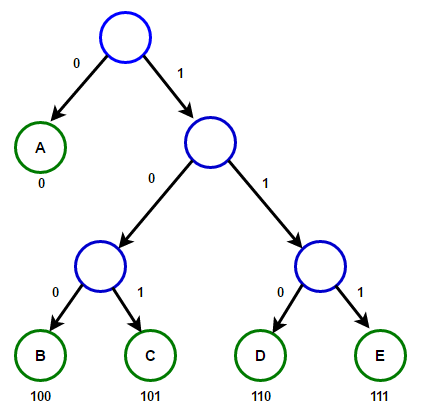
Рассмотрим некоторый текст, состоящий только из ‘A’ , ‘B’ , ‘C’ , ‘D’ , а также ‘E’ символов, а их частота 15 , 7 , 6 , 6 , 5 , соответственно. Следующие рисунки иллюстрируют шаги, за которыми следует алгоритм:

Путь от корня к любому конечному узлу хранит оптимальный код префикса (также называемый кодом Хаффмана), соответствующий символу, связанному с этим конечным узлом.

Реализация

Ниже приведена реализация алгоритма сжатия кода Хаффмана на C++, Java и Python:

Источник