Основы деревьев решений
Дерево решений строитсярекурсивное разбиение— начиная с корневого узла (известного как первыйродитель), каждый узел может быть разделен на левый и правыйребенокузлы. Эти узлы затем могут быть дополнительно разделены, и они сами становятся родительскими узлами своих результирующих дочерних узлов.
Например, глядя на изображение выше, корневой узел Work to do? и расщепляется на дочерние узлы Stay in а также Outlook основанный на том, есть или нет работа, чтобы сделать. Outlook Узел далее делится на три дочерних узла.
Итак, как мы узнаем, какова оптимальная точка расщепления в каждом узле?
Начиная с корня, данные разделяются на функцию, которая приводит к наибольшемуПолучение информации(И.Г.) (объяснено более подробно ниже). В итерационном процессе мы затем повторяем эту процедуру расщепления на каждомдочерний узелдо тех пор, пока листья не станут чистыми — то есть все образцы в каждом узле принадлежат одному и тому же классу.
На практике это может привести к очень глубокому дереву со многими узлами, что может легко привести к переоснащению. Таким образом, мы обычно хотимчерносливдерево, установив предел для максимальной глубины дерева.
Максимизация получения информации
Чтобы разделить узлы на наиболее информативные функции, нам нужно определить целевую функцию, которую мы хотим оптимизировать с помощью алгоритма обучения дерева. Здесь нашей целевой функцией является максимизация получения информации при каждом разделении, которое мы определяем следующим образом:
Вот,еэто функция для выполнения раскола,Dp,Dleft, а такжеDrightнаборы данных родительского и дочернего узлов,яэтомера загрязненности,Npобщее количество выборок в родительском узле, иNleftа такжеNRightколичество выборок в дочерних узлах.
Мы обсудим меры примеси для деревьев решений классификации и регрессии более подробно в наших примерах ниже. Но пока, просто поймите, что прирост информации — это просто разница между примесью родительского узла и суммой примесей дочернего узла — чем меньше примесей дочерних узлов, тем больше прирост информации.
Обратите внимание, что приведенное выше уравнение предназначено для бинарных деревьев решений — каждый родительский узел разделен только на два дочерних узла. Если у вас есть дерево решений с несколькими узлами, вы просто суммируете нечистоту всех узлов.
Деревья классификации
Мы начнем с разговора о деревьях решений классификации (также известных какдеревья классификации). Для этого примера мы будем использовать Ирис набор данных, классика в области машинного обучения. Он содержит измерения 150Ирисцветы из трех разных видов —Setosa,радужный, а такжеVirginica, Это будут нашицели, Наша цель — предсказать, какая категорияИрисцветок принадлежит. Длина и ширина лепестка в сантиметрах хранятся в виде столбцов, которые мы также называемфункциииз набора данных.
Давайте сначала импортируем набор данных и назначим функции как X и цель как y :
Вот,р (я | т)доля образцов, принадлежащих к классусдля конкретного узлаT, Следовательно, энтропия равна 0, если все выборки в узле принадлежат одному и тому же классу, и энтропия максимальна, если мы имеем равномерное распределение классов.
Для более наглядного понимания энтропии построим индекс примесей для диапазона вероятностей [0, 1] для класса 1. Код выглядит следующим образом:
Как видите, энтропия равна 0, еслиp (i = 1 | t) = 1, Если классы распределены равномерно сp (i = 1 | t) = 0,5Энтропия равна 1.
Теперь вернемся к нашемуИрисНапример, мы визуализируем наше обученное дерево классификации и увидим, как энтропия решает каждое разделение.
Хорошая особенность в scikit-learn является то, что это позволяет нам экспортировать дерево решений в виде .dot файл после тренировки, который мы можем визуализировать, используя GraphViz, например. В дополнение к GraphViz, мы будем использовать библиотеку Python под названием pydotplus , который имеет возможности, аналогичные GraphViz и позволяет нам конвертировать .dot файлы данных в файл изображения дерева решений.
Вы можете установить pydotplus а также graphviz выполнив следующие команды в вашем терминале:
pip3 install pydotplus
apt install graphviz
Следующий код создаст изображение нашего дерева решений в формате PNG:
Глядя на результирующую фигуру дерева решений, сохраненную в файле изображения tree.png Теперь мы можем хорошо проследить разбиения, которые дерево решений определило из нашего обучающего набора данных. Мы начали с 150 выборок в корне и разделили их на два дочерних узла с 50 и 100 выборками, используяширина лепесткаотсечка ≤ 1,75 см. После первого разделения мы видим, что левый дочерний узел уже чист и содержит только выборки из setosa класс (энтропия = 0). Дальнейшие расщепления справа затем используются для отделения образцов от versicolor а также virginica учебный класс.
Глядя на конечную энтропию, мы видим, что дерево решений с глубиной 4 очень хорошо справляется с разделением классов цветов.
Деревья регрессии
Мы будем использовать Бостон Жилье набор данных для нашего примера регрессии. Это еще один очень популярный набор данных, который содержит информацию о домах в пригороде Бостона. Есть 506 образцов и 14 атрибутов. Для простоты и наглядности мы будем использовать только два — MEDV (средняя стоимость домов, занимаемых владельцами, в 1000 долл. США) в качестве цели и LSTAT (процент от более низкого статуса населения) как особенность.
Давайте сначала импортируем необходимые атрибуты из scikit-learn в pandas DataFrame.
Давайте использовать DecisionTreeRegressor реализовано в scikit-learn обучить дерево регрессии:
Вот,Ntколичество обучающих выборок в узлеT,Dtэто обучающее подмножество в узлеT,у (я)является истинным целевым значением, иYTЯвляется прогнозируемой целевой величиной (выборочное среднее):
Теперь давайте смоделируем отношения между MEDV а также LSTAT чтобы увидеть, как выглядит линия соответствия дерева регрессии:
Как мы видим на полученном графике, дерево решений глубины 3 отражает общую тенденцию в данных.
Я надеюсь, вам понравился этот урок по деревьям решений! Мы обсудили фундаментальные концепции деревьев решений, алгоритмы минимизации примесей и способы построения деревьев решений как для классификации, так и для регрессии.
На практике важно знать, как выбрать подходящее значение для глубины дерева, чтобы оно не соответствовало или не соответствовало данным. Зная, как объединить деревья решений, чтобы сформировать ансамбльслучайный лестакже полезно, так как обычно имеет лучшую производительность обобщения, чем отдельное дерево решений, из-за случайности, которая помогает уменьшить дисперсию модели. Он также менее чувствителен к выбросам в наборе данных и не требует особой настройки параметров.
Мы рассмотрим эти методы в нашемМашинное обучение Pythonсерии, а также погружение в другие модели машинного обучения, такие как персептроны, Adaline, линейная и полиномиальная регрессия, логистическая регрессия, SVM, ядра SVM, k-ближайшие соседи, модели для анализа настроений, кластеризация k-средних, DBSCAN, сверточная нейронная сеть сети и периодические нейронные сети.
Мы также рассмотрим другие темы, такие как регуляризация, обработка данных, выбор и извлечение функций, уменьшение размерности, оценка моделей, методы ансамблевого обучения и развертывание модели машинного обучения.
Источник
Введение в деревья классификации и регрессии
Когда взаимосвязь между набором переменных-предикторов и переменной отклика является линейной, такие методы, как множественная линейная регрессия , могут создавать точные прогностические модели.
Однако, когда взаимосвязь между набором предикторов и откликом сильно нелинейна и сложна, нелинейные методы могут работать лучше.
Одним из таких примеров нелинейного метода являются деревья классификации и регрессии , часто сокращенно CART .
Как следует из названия, модели CART используют набор переменных-предикторов для построения деревьев решений, которые предсказывают значение переменной отклика.
Например, предположим, что у нас есть набор данных, содержащий переменные-предикторы «Сыгранные годы» и « Среднее количество хоум-ранов » вместе с переменной-ответом « Годовая зарплата » для сотен профессиональных бейсболистов.
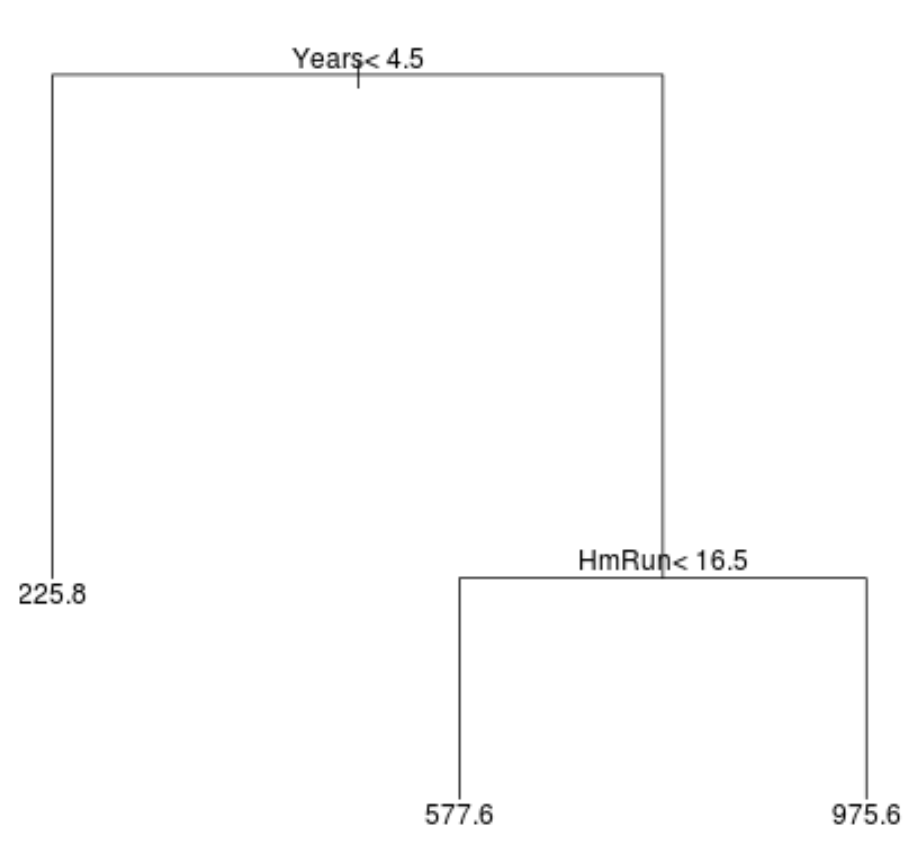
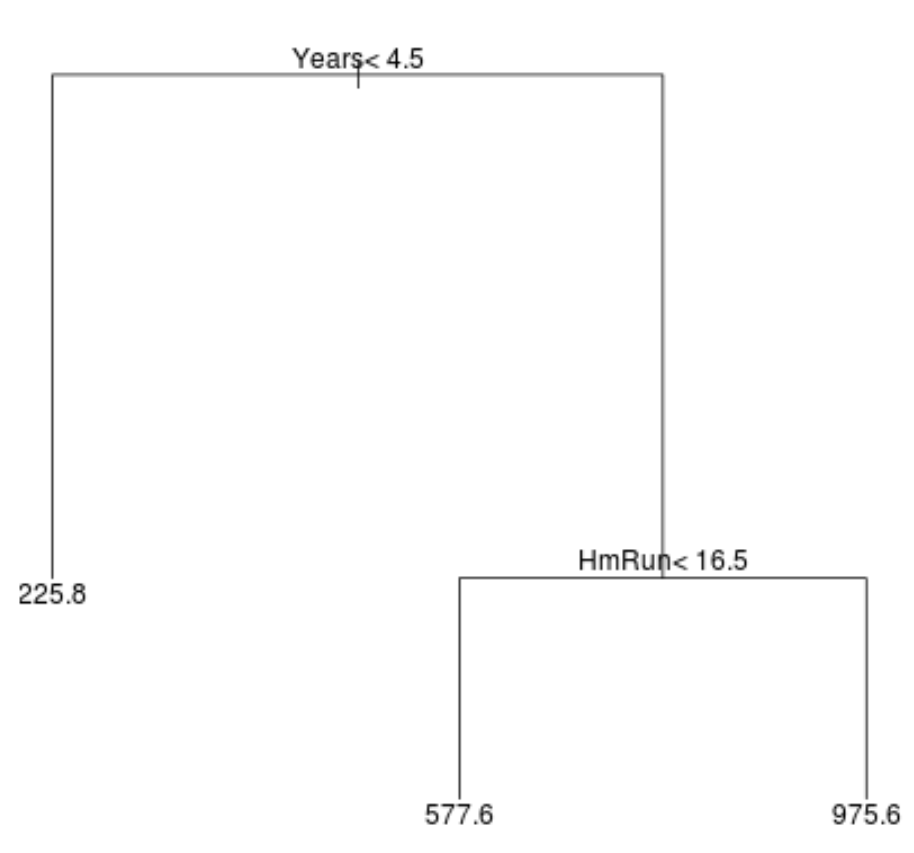
Вот как может выглядеть дерево регрессии для этого набора данных:
Способ интерпретации дерева следующий:
- Прогнозируемая зарплата игроков, играющих менее 4,5 лет, составляет 225,8 тысяч долларов.
- Прогнозируемая зарплата игроков со стажем игры более или равным 4,5 года и средним показателем хоумранов менее 16,5 имеет прогнозируемую зарплату в размере 577,6 тыс. долларов.
- Прогнозируемая зарплата игроков с 4,5 годами игры и средним хоум-раном 16,5 или выше имеет прогнозируемую зарплату в размере 975,6 тыс. долларов.
Результаты этой модели интуитивно понятны: игроки с большим стажем и более средними хоум-ранами, как правило, получают более высокие зарплаты.
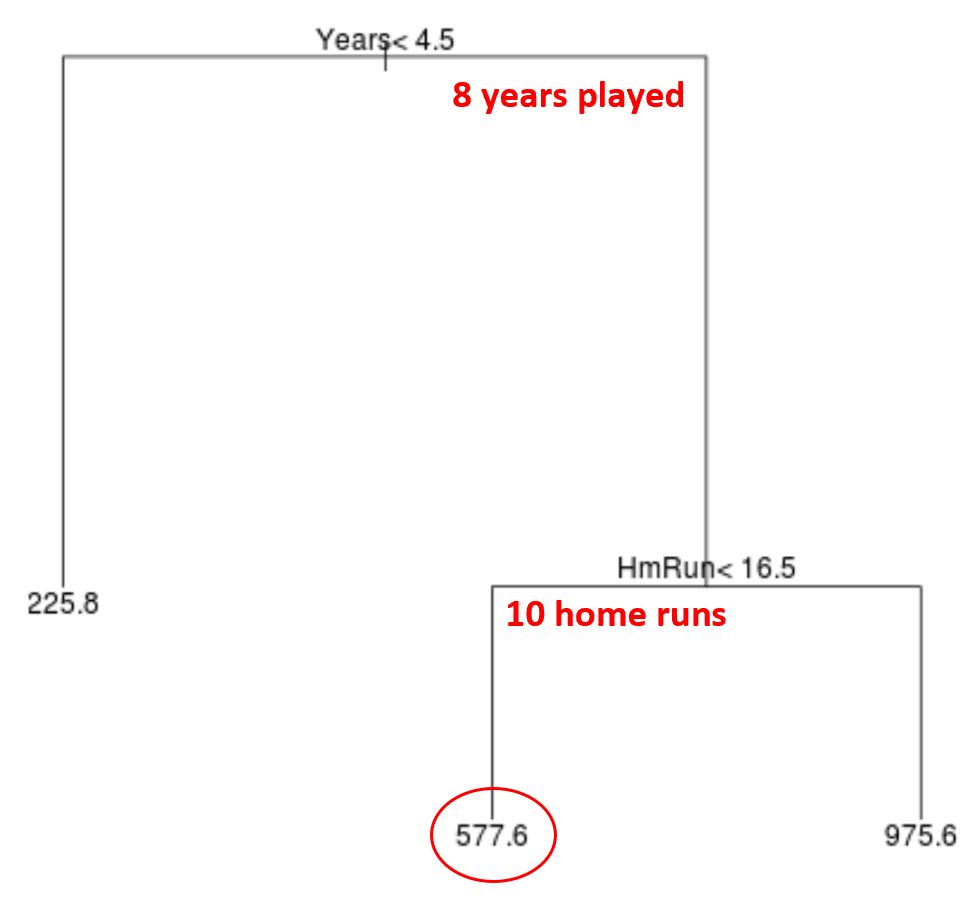
Затем мы можем использовать эту модель для прогнозирования зарплаты нового игрока.
Например, предположим, что данный игрок играет 8 лет и совершает в среднем 10 хоум-ранов в год. Согласно нашей модели, мы прогнозируем, что годовая зарплата этого игрока составит 577,6 тыс. долларов.
- Первая предикторная переменная в верхней части дерева является наиболее важной, т. е. наиболее влиятельной при прогнозировании значения переменной отклика. В этом случае сыгранные годы могут предсказать зарплату лучше, чем средний хоум -ран.
- Области в нижней части дерева известны как конечные узлы.Это конкретное дерево имеет три конечных узла.
Шаги по созданию моделей CART
Мы можем использовать следующие шаги для построения модели CART для данного набора данных:
Шаг 1: Используйте рекурсивное двоичное разбиение, чтобы вырастить большое дерево на обучающих данных.
Во-первых, мы используем жадный алгоритм, известный как рекурсивное бинарное разбиение, чтобы вырастить дерево регрессии, используя следующий метод:
- Рассмотрим все переменные-предикторы X 1 , X 2 , …, X p и все возможные значения точек отсечения для каждого из предикторов, затем выберем предиктор и точку отсечения так, чтобы результирующее дерево имело наименьшую RSS (остаточную стандартную ошибку) .
- Для деревьев классификации мы выбираем предиктор и точку отсечения таким образом, чтобы результирующее дерево имело наименьшую частоту ошибочной классификации.
- Повторите этот процесс, останавливаясь только тогда, когда каждый конечный узел имеет меньше некоторого минимального количества наблюдений.
Этот алгоритм является жадным , потому что на каждом шаге процесса построения дерева он определяет наилучшее разбиение, основываясь только на этом шаге, вместо того, чтобы заглядывать вперед и выбирать разбиение, которое приведет к лучшему общему дереву на каком-то будущем шаге.
Шаг 2: Примените сокращение сложности стоимости к большому дереву, чтобы получить последовательность лучших деревьев в зависимости от α.
После того, как мы вырастили большое дерево, нам нужно обрезать дерево, используя метод, известный как сокращение сложности стоимости, который работает следующим образом:
- Для каждого возможного дерева с T концевыми узлами найдите дерево, которое минимизирует RSS + α|T|.
- Обратите внимание, что по мере увеличения значения α деревья с большим количеством конечных узлов оштрафованы. Это гарантирует, что дерево не станет слишком сложным.
Результатом этого процесса является последовательность лучших деревьев для каждого значения α.
Шаг 3: Используйте k-кратную перекрестную проверку, чтобы выбрать α.
Как только мы нашли лучшее дерево для каждого значения α, мы можем применить k-кратную перекрестную проверку , чтобы выбрать значение α, которое минимизирует ошибку теста.
Шаг 4: Выберите окончательную модель.
Наконец, мы выбираем окончательную модель, соответствующую выбранному значению α.
Плюсы и минусы моделей CART
Модели CART предлагают следующие преимущества :
- Их легко интерпретировать.
- Их легко объяснить.
- Их легко визуализировать.
- Их можно применять как к задачам регрессии, так и к задачам классификации .
Однако модели CART имеют следующие недостатки:
- Они, как правило, не обладают такой высокой точностью прогнозирования, как другие алгоритмы нелинейного машинного обучения. Однако, агрегируя множество деревьев решений с помощью таких методов, как бэггинг, бустинг и случайные леса, можно повысить точность их прогнозирования.
Источник