Программирование 2 курс / Программирование(4172,4173) / Лекции / Лекция 22.Обход графа
В некоторых задачах необходимо обойти дерево или граф в определенном порядке с посещением один раз каждой вершины для выполнения некоторой операции, например поиска чего-либо.
Обход (поиск) в графах и деревьях можно выполнять в ширину и в глубину. Для деревьев (особенно бинарных) часто используют еще обходы сверху, снизу и слева направо.
Обход в ширину (дерева и графа) происходит по уровням: сначала посещается вершина уровня 0 (заданная начальная вершина обхода vn), затем вершины уровня 1, находящиеся на расстоянии в 1 шаг от начальной вершины, затем – вершины уровня 2, расположенные на 2 шага от начала обхода, т. е. на 1 шаг от вершин уровня 1 и т. д. Уровень i+1 включает преемников вершин уровня i (рис. 22.1).
Обход в ширину выполняется с помощью очереди вершин на посещение. Из головы очереди выбирается и посещается вершина, а ее преемники заносятся в хвост очереди.
Пока из очереди выбираются и посещаются все вершины уровня i, за ними в очереди расположатся все вершины уровня i+1. Первоначально в очередь помещается единственная вершина уровня 0. В дереве это корень, а в графе — заданная начальная вершина обхода vn . На удивление простой и изящный алгоритм!
Обход графа в ширину можно рассматривать как обход в ширину дерева его путей, начинающихся с заданной вершины. (рис. 22.1).
Подобный обход иногда называют “волновым алгоритмом”, т.к. последовательность обхода напоминает круговые волны от брошенного в воду камня.
Обходы в ширину:
Рис. 22.1. Обход графа в ширину
Алгоритм обхода дерева в ширину для обхода графа дополняется учетом посещений: при записи в очередь на посещение вершина j отмечается в векторе p, чтобы избежать ее повторного посещения. Так получен алгоритм 22.1.
На рис. 22.2 показано дерево кратчайших путей от всех вершин графа до вершины 1, которая является началом обхода.
Алгоритм 22.1. Обход связного графа (орграфа) в ширину,
#define NOV -1 /* Вершина новая — не была в очереди */
int p[n]; /* Учет посещений; пути к началу обхода */
/* Подпрограмма обхода графа в ширину, начиная с вершины vn */
void obhod_gr_sh (int vn)
< Очередь ==>v; Посетить v; /* выполняется n раз */
if (p[j]==NOV) /* выполняется m раз */
> while (Очередь != пусто); /* выполняется n раз */
obhod_gr_sh (vn); /* Обход графа, начиная с vn */
Обозначение: for (x S) . . . – это цикл, выполняемый для каждого элемента x из множества S ( — «принадлежит»).
При этом удобно в p[j] записывать номер вершины v, предшествующей j на пути к j от начала обхода. Этот путь является кратчайшим, т. к. обход ведется по уровням, и на предыдущих уровнях вершина j не встретилась (т.е. за меньшее число шагов до нее дойти невозможно).
Первоначально вектор p заполняется значениями NOV, обозначающими новые вершины, еще не записанные в очередь на посещение.
В результате вектор p будет содержать дерево кратчайших путей от каждой вершины графа до начальной вершины (вот вам еще один метод хранения дерева – с одной ссылкой, дуги направлены к корню).
Кратчайший путь из i в vn — последовательность v[1], . , v[L], где v[1]=i, v[L]=vn, v[k]=p[v[k-1]] для k>1.
vn = 1 j = 0 1 2 3 4
- 3
/ \ 2 4 1 3 Рис. 22.2. Дерево кратчайших путей графа к вершине 1 Для несвязного графа алгоритм 20.1 посещает вершины только той компоненты связности, в которой начат обход (он позволяет находить компоненты связности). Посещение всех вершин графа обеспечивает алгоритм 20.2. Алгоритм 22.2. Обход графа (орграфа) в ширину for (i=0; ifor (vn=1; vnif (p[vn]==NOV) obhod_gr_sh(vn); /* Обход, начиная с vn */ Для поиска пути между двумя вершинами графа обход в ширину удобнее, чем в глубину, т. к. дает кратчайший путь. Обход в глубинуОбход в глубину графа, как и дерева, выполняется по принципу: если можно – вперед (вглубь) к преемнику, дальше от начала обхода, иначе — назад к предшествующей вершине на пути от начала обхода. Пример 22.1. Рассмотрим обход графа в глубину на примере следующей задачи. Найти кратчайший цикл в графе. На рис. 20.4 показан граф, содержащий циклы (замкнутые пути) длины пять: 1, 2, 4, 5, 3, 1; длины четыре: 1, 2, 4, 3, 1 и длины три: 3, 4, 5, 3. Длина пути — количество ребер. 1 3 5 

Источник
Три алгоритма на графах
Пусть G=(V,E) — ориентированный граф , для каждого ребра 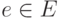
Естественно спросить, как узнать длину кратчайшего пути из a в b и построить его? Лучшие известные на сегодняшний день алгоритмы, отвечающие на этот вопрос, решают, на самом деле, более общую задачу построения всех кратчайших путей из одного источника: по вершине a найти длины кратчайших путей из a во все достижимые из нее вершины и построить для каждой из таких вершин некоторый кратчайший путь из a . Если для каждой вершины , достижимой из a , зафиксировать один кратчайший путь из a в v , то получившийся граф будет представлять ориентированное дерево с корнем a (докажите это!). Это дерево называется деревом кратчайших путей из a .
Мы рассмотрим алгоритм построения дерева кратчайших путей и определения их длин, предложенный в 1959г. Е. Дейкстрой. Его идея следующая: перед каждым этапом известно множество отмеченных вершин S , для которых кратчайшие пути найдены ранее; тогда на очередном этапе к нему добавляется вершина w , с самым коротким путем из a , проходящим по множеству S ; после этого пересчитываются длины кратчайших путей из a в оставшиеся вершины из V \ S с учетом новой вершины w . Длина текущего кратчайшего пути из a в v , проходящего по множеству S , заносится в ячейку D[v] массива D . В конце работы в этом массиве отыскиваются длины соответствующих кратчайших путей . Для определения дерева кратчайших путей служит массив ОТЕЦ , его элемент ОТЕЦ[v] содержит ссылку на вершину, из которой кратчайший путь приходит в v .
Вход: G=(V,E) — ориентированный граф , c(u,v) >= 0 — длина ребра 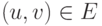

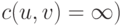
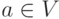
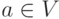
Пример 11.3. Рассмотрим работу этого алгоритма на нагруженном графе G=(V=, E) и выделенной вершине . Зададим длины ребер матрицей C= (cuv) , где элемент cuv=c(u,v) :
Дерево кратчайших путей из вершины a задается массивом ОТЕЦ . Оно представлено на рис. 11.5. Теорема 11.4. (о корректности алгоритма Дейкстры ) Алгоритм Дейкстры строит дерево кратчайших путей из вершины a во все достижимые из нее вершины и для каждой такой вершины v определяет длину D[v] кратчайшего пути в нее из a . Доказательство Докажем по индукции, что после каждого этапа алгоритма выполнены следующие условия: Эти три условия очевидно выполняются после инициализации в строках 1- 5. Предположим теперь, что они выполнены перед началом k -го этапа. Пусть w — вершина , добавляемая к S на k -ом этапе. По предположению, D[w] — длина кратчайшего пути из a в w , все вершины которого, кроме w , входят в S . Предположим, что есть другой более короткий путь p из a в w . Зафиксируем на этом пути первую вершину u , не входящую в S . По выбору p . Поэтому путь p разбивается на две непустые части: путь p1 из a в u и путь p2 из u в w . Но по выбору w мы имеем, что длина p1 >= D[u] >= D[w] . Так как длина p2 неотрицательна, то длина p >= D[w] , т.е. этот путь не короче пути, представленного в дереве T . Таким образом, D[w] — это длина кратчайшего пути из a в w . Следовательно, условие (а) выполнено и после k -го этапа. Рассмотрим теперь произвольную вершину Так как после завершения алгоритма S = V , то в завершающем дереве T представлены кратчайшие пути из a во все достижимые из нее вершины, а массив D содержит длины этих путей. Значение указывает на то, что вершина u не достижима из вершины a . Замечание о сложности. На каждом этапе (исполнении тела основного цикла в стр. 6 — 13) одна вершина добавляется во множество S . Поэтому таких этапов не более |V| . Чтобы выбрать в массиве D вершину w с минимальным D[w] (стр. 7), требуется не более |V| шагов. Перевычисление D[u] для каждой из вершин требует константного числа операций, поэтому весь цикл в стр. 9 — 12 потребует не более c |V| шагов. Отсюда получаем, что для некоторой константы c время выполнения алгоритма Дейкстры не превышает c |V| 2 . Поскольку размер любого представления исходного графа не меньше |V| , то алгоритм работает в квадратичное время (от размера входа). Источник![\[\left( \begin</p></noscript> <p> &a& b& c & d & e & f \\ a &0 & 25& 5 & 30 & \infty & 75\\ b &12 & 0& \infty & \infty & 120 & 20\\ c &\infty & 15& 0 & 20 & 45 & 60\\ d &\infty & \infty& \infty & 0 & 23 & 20\\ e & \infty & \infty & 75 & 20 & 0 & 20\\ f & 40 & 15& 15 & 26 & \infty & 0 \end \right) \]»/></p> <p>Поэтапную работу алгоритма Дейкстры удобно представлять в виде таблицы, строки которой соответствуют его этапам. Первый столбец — номер этапа, второй показывает изменение множества отмеченных вершин S , третий — вершину w , добавляемую к S на текущем шаге, четвертый — длину кратчайшего пути из a в w , затем идут столбцы со значениями элементов массивов D и ОТЕЦ .</p> <table border=](https://intuit.ru/sites/default/files/tex_cache/d1a56d3913f80f422a60fed496cae224.png) Таблица 11.1. Алгоритм Дейкстры на графе G.
Таблица 11.1. Алгоритм Дейкстры на графе G. N S w D[w] D ОТЕЦ b c d e f b c d e f 1. a c 5 25 5 30 
75 a a a — a 2. a, c b 20 20 — 25 50 65 c a c c c 3. a, c, b d 25 — — 25 50 40 c a c c b 4. a, c, b,d f 45 — — — 48 45 c a c d b 5. a, c, b,d e 45 — — — — 45 c a c d b


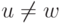

![S \cup \< w\></noscript>»/>, либо не включает вершину w и в этом случае его длина равна D[u] и он имеется в текущем дереве T , либо он проходит через w и составлен из кратчайшего пути из a в w через S , продолженного ребром (w,u) . В последнем случае длина пути равна D[w] + c(w,u) . Но в 10-ой строке алгоритма эти величины сравниваются и, если путь через w короче, то его длина становится новым значениием D[u] (строка 11) и он фиксируется в дереве T (строка 12). Следовательно, условия (б) и (в) также выполнены после k -го этапа.</p> <p><img decoding=](https://intuit.ru/sites/default/files/tex_cache/88e63f3e95a8427f7627cdf70521f228.png)
![D[u]= \infty](https://intuit.ru/sites/default/files/tex_cache/d6d6844bf617078a96ba91421946f8de.png)