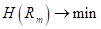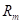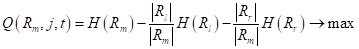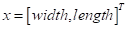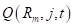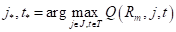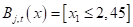Критерии качества для построения решающих деревьев
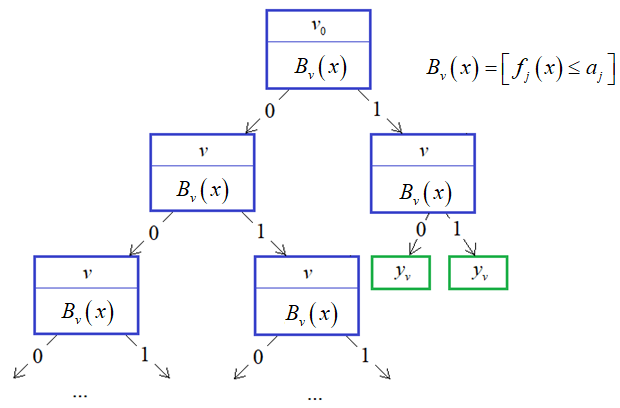
На предыдущем занятии мы с вами познакомились с общей идеей логических методов. Здесь же продолжим эту тему и подробнее поговорим о бинарных решающих деревьях. Приведу пример такого дерева из предыдущего занятия:
Фактически это связный ациклический граф, в котором есть корень, внутренние вершины и листы (вершины без потомков). Причем, каждая внутренняя вершина имеет ровно два ответвления, соответствующие стрелкам «да» и «нет». Именно поэтому дерево с такой структурой называют бинарным.
Если у нас есть уже построенное дерево по множеству данных, то логический вывод делается очень просто. Предположим, мы классифицируем вектор
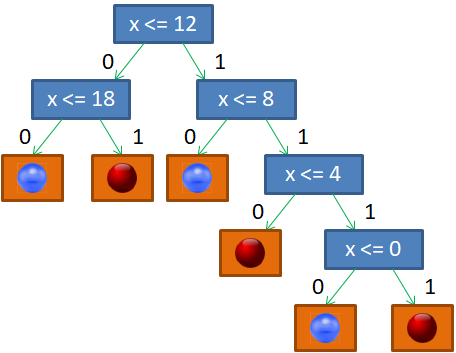
с n признаками. Тогда, начиная с корневой вершины , проверяем предикат:
То есть, мы смотрим на j-й признак для вектора 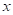
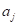
В следующей промежуточной вершине повторяем этот процесс и с помощью предиката проверяем значение другого j-го признака (или того же самого). В зависимости от ответа, переходим или по стрелке 1, или по стрелке 0.
Как только дошли до листа, относим вектор к тому классу, который прописан в текущем листе. Процесс логического вывода на этом завершается. Именно поэтому листовые вершины еще называют терминальными.
Однако, чтобы проделать такой вывод, мы с вами должны знать структуру дерева, набор предикатов для каждой промежуточной вершины и иметь правильные значения в листовых вершинах. Листы дерева, как правило, хранят определенные числа. Они могут означать или номер (метку) класса, или константное значение функции при решении задач регрессии. Но пока будем полагать, что в них записаны метки класса.
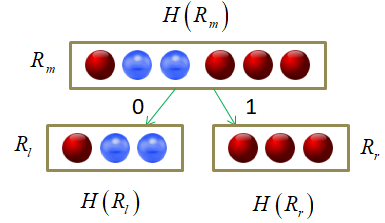
Итак, главный вопрос, как построить бинарное решающее дерево по множеству данных обучающей выборки ? Чтобы лучше понимать этот процесс, давайте возьмем очень простой пример разбиения последовательности красных и синих шаров, собственно, на красные и синие:
Здесь вектор состоит из одной компоненты и представляет собой число – номер позиции шара. Это единственный признак, по которому можно выполнять разбиение данной последовательности. В каждой промежуточной вершине бинарного решающего дерева будет использован предикат вида:
И, так как признак всего один, то . Остается найти только нужные пороги t.
Если бы разбиение делал я сам, то предложил бы следующее решающее дерево:
Почему именно так? В действительности, можно было бы придумать и другие варианты. Я руководствовался простым принципом: в каждой вершине порог t следует выбирать так, чтобы в одной части было как можно больше представителей только одного какого-либо класса (шаров одного цвета), а в другой – все оставшиеся. То есть, это некий критерий здравого смысла, естественная эвристика, которая сокращает глубину дерева. Но вы можете сказать, а зачем нам минимизировать глубину решающего дерева? Пусть оно получается таким, каким сделает его алгоритм. Например, будем поочередно перебирать пороги t от 0 до 19 и рано или поздно гарантированно разобьем последовательность шаров на красные и синие. Да, дерево будет значительно глубже, ну и что? Однако, здесь всегда следует помнить, что данная последовательность всего лишь обучающая выборка. Мы предполагаем использовать это дерево и для других подобных последовательностей с несколько другим распределением синих и красных шаров. Иначе, это была бы не задача машинного обучения, а просто разбиение конкретной выборки. Так вот, можно заметить, что чем меньше глубина решающего дерева, тем меньше используется порогов разбиения и тем выше, в среднем, обобщающая способность такого дерева. Именно поэтому стараются строить деревья минимальной глубины.
Но как это сделать? В самом простом варианте можно выполнить полный перебор всех возможных разбиений и выбрать дерево минимальной глубины. Для нашей задачи это еще как-то можно было бы реализовать. Но, как вы понимаете, в общем случае, это займет так много времени, что не хватит и жизни всего человечества. Поэтому здесь нужно искать другие подходы.
Если вернуться к моему варианту бинарного дерева, то, как я отмечал, в каждой промежуточной вершине старался порог t выбирать так, чтобы в одной части было как можно больше представителей одного класса (шаров одного цвета), а в другой как получится, т.е. все оставшиеся. Это некая эвристика. Наша цель, наделить алгоритм примерно такой же эвристикой. Как это сделать? Математики обратили свои взоры в ранние наработки самых разных формул и представили миру несколько критериев качества предикатов. Одним из популярных стала энтропия:
где — вероятность i-го класса; N – общее число классов (в нашем примере – цветов шаров). Известно, что эта величина является некой характеристикой хаотичности системы. Чем больше разнообразия, тем выше энтропия, и наоборот, чем больше порядка, тем она меньше. Ее можно естественным образом использовать для оценки характеристики текущего разбиения каждой вершины. Например:
Такую характеристику в решающих деревьях называют impurity (информативностью). Чем она меньше, тем лучше (качественнее) набор данных в вершине. И, наоборот, чем она больше, тем разнообразнее (хаотичнее) данные в вершине.
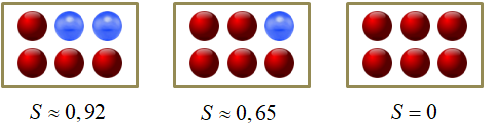
Вернемся, теперь, к примеру разбиения последовательности красных и синих шаров. Последовательность состоит из N=2 классов с вероятностями появления каждого из них:
Следовательно, impurity (в данном случае энтропия) корневой вершины дерева, равна:
Далее, мы выбираем предикат с порогом t = 12:
и получаем две подвыборки с impurity (энтропиями):
Величина 0,6 значительно меньше начального значения 0,993, а значит, во второй последовательности больше порядка, чем в исходной. И это очень хорошо. Именно этого мы и добиваемся, выбирая порог t.
Теперь, нам нужно на основе величин сформировать единый критерий (одно число), по которому мы бы судили о качестве разбиения выборки на две подвыборки. Это также можно выполнить различными способами, но часто используется следующая формула под названием информационный выигрыш (information gain):
где 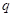
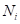
Если посчитать этот критерий для других порогов t, то окажется, что при t = 12 имеем наибольшее значение. А, значит, наилучшее разбиение с точки зрения выбранных критериев: энтропии и информационного выигрыша.
Математически поиск наилучшего предиката в текущей вершине дерева, можно записать так:
Или, в общем случае, учитывая, что мы подбираем не только пороги, но и признаки , по которым делятся объекты на две подвыборки, имеем:
А в качестве impurity, помимо энтропии также используют:
- критерий Джини (Gini impurity):
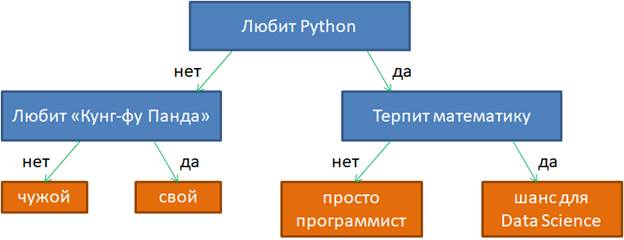
, здесь
— вероятность (частота) появления объектов k-го класса в вершине дерева;
- ошибка классификации (misclassification error):
.
(Критерий Джини не следует путать с индексом Джини, о котором мы ранее говорили – это две совершенно разные характеристики.) На практике критерий Джини работает почти также, как и энтропия. Это хорошо видно из графиков данных критериев при бинарной классификации: 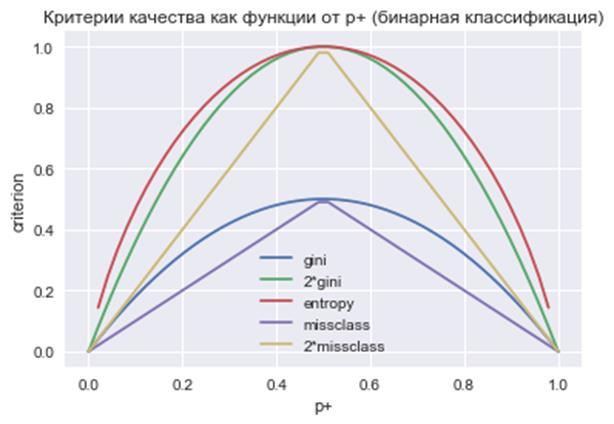
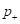
Источник
Построение решающих деревьев жадным алгоритмом ID3
На предыдущем занятии мы с вами познакомились с критериями выбора предикатов для разбиения множества данных в вершинах решающего дерева. В первую очередь – это impurity (информативность, мера неопределенности), обозначим ее через
где — выборка, попавшая в текущую вершину. И показатель качества разбиения, который часто вычисляется как информационный выигрыш:
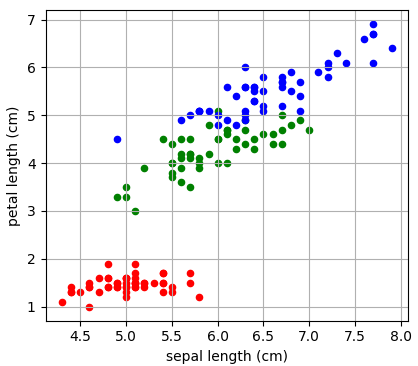
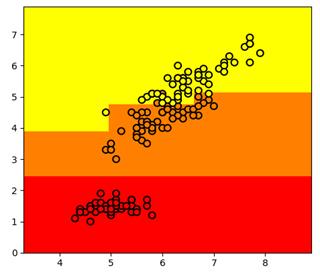
Давайте теперь воспользуемся этими показателями для построения бинарного решающего дерева. В качестве обучающей выборки возьмем 150 объектов трех классов ирисов (50 в каждом классе), распределенных в двумерном признаковом пространстве: длина и ширина лепестков:
То есть, входные векторы будут иметь два числовых признака:
Существует несколько распространенных алгоритмов построения решающих деревьев. Вначале я рассмотрю самый простой, который называется ID3 (Iterative Dichotomiser 3), разработанный Россом Куинланом в 1986 году для задачи классификации. Этот алгоритм использует энтропию в качестве информативности и реализует жадную стратегию, то есть, в каждом узле дерева, начиная с корневого, находит такой признак j и такой порог t, которые дают наибольшее значение показателя :
Затем, построение рекурсивно повторяется для каждой новой вершины.
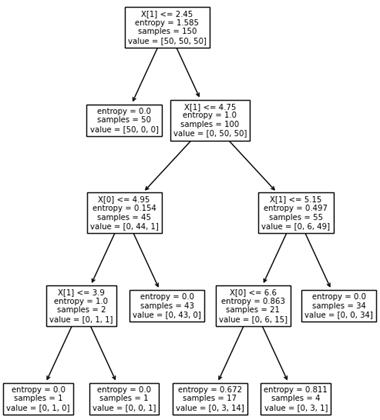
Вот пример разбиения обучающего множества деревом глубиной 4. Само дерево имеет вид:
Отсюда хорошо видно, как происходило разбиение. Вначале были отделены все красные объекты выборки по второму признаку (длина лепестка) с порогом t = 2,45 и предикатом:
Если предикат выполняется, то попадаем в листовую вершину с нулевой энтропией и 50-ю представителями класса «красных» объектов. Во вторую вершину попадает 100 объектов двух других классов с энтропией, равной 1. Далее, мы делим объекты второй вершины дерева также по второму признаку и уровню 4,75. Формируются следующие две вершины. И так далее, пока либо не будет достигнута нулевая энтропия и сформирован лист дерева, либо глубина дерева достигнет уровня 4. (Этот максимальный уровень был задан при генерации данного решающего дерева.) В каждой листовой вершине мы сохраняем метку класса с наибольшим числом представителей.
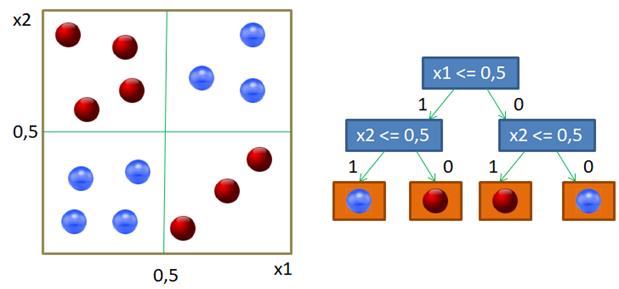
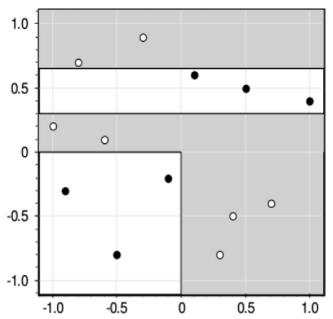
Вот наглядный пример работы жадного алгоритма ID3. Казалось бы, все прекрасно и ничто не мешает нам использовать его в самых разных задачах. Однако, практика показала, что жадная стратегия построения деревьев часто не самая лучшая. Простой контрпример – задача XOR, когда объекты двух классов сосредоточены в разных углах квадрата:
Жадная стратегия дает, следующее решающее дерево:
Но, тем не менее, алгоритм ID3 относительно прост в реализации, а потому является основой для более сложных подходов к построению решающих деревьев, о которых мы поговорим на следующих занятиях.
Критерии останова (методы регуляризации)
- impurity равна нулю или меньше некоторого заданного значения;
- число объектов в вершине меньше заданной величины;
- вероятность правильной классификации объекта больше заданной величины;
- достигнуто максимальное количество листьев в дереве;
- достигнута максимальная заданная глубина дерева.
Преимущества и недостатки жадной стратегии
Итак, я думаю, в целом идея построения решающих деревьев по алгоритму ID3 вам понятна. В заключение отмечу преимущества и недостатки такого подхода.
Достоинства:
- Интерпретируемость и простота классификации (легко объяснить результат классификации эксперту).
- Допустимы разнотипные данные и пропуски в данных.
- Не бывает отказов от классификации.
Недостатки:
- Жадная стратегия в большинстве задач излишне усложняет структуру дерева, то есть, приводит к его переобучению.
- Чем дальше от корня дерева, тем меньше объектов в листовых вершинах, а значит, ниже статистическая надежность различных показателей, например, вероятности появления того или иного класса.
- Высокая чувствительность к шуму в объектах выборки и критерию информативности (impurity).
Источник
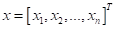
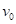
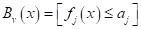
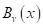
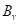
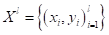

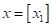
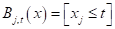
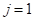
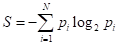
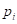
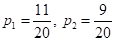
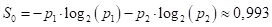
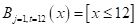
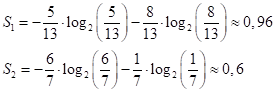
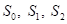
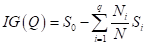
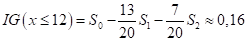
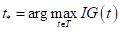
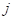
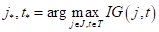
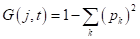 , здесь
, здесь 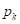 — вероятность (частота) появления объектов k-го класса в вершине дерева;
— вероятность (частота) появления объектов k-го класса в вершине дерева;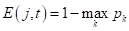 .
.