Дерево маркировки сети петри

На этом шаге мы рассмотрим вопросы, связанные с достижимостью и покрываемостью в сетях Петри .

Определение. Задача достижимости. Для данной сети Петри С = (P, T, I, O) с маркировкой m и маркировки m’ определить: m’ , принадлежащее R(C, m) .

Задача достижимости — основная задача анализа сети Петри. Многие задачи анализа могут быть сформулированы в терминах такой задачи достижимости.

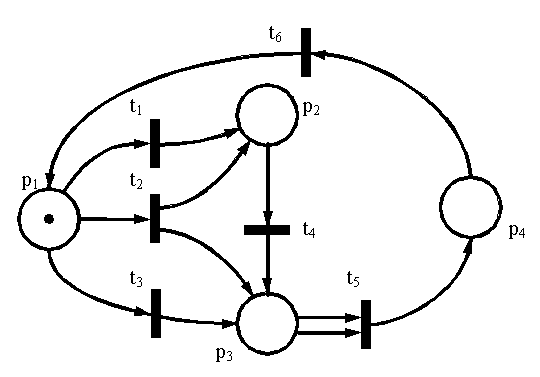
Множество достижимости сети Петри представляет собой дерево достижимости. Пусть имеется сеть Петри, представленная на рисунке 1.

Рис.1. Маркированная сеть Петри, для которой строится дерево достижимости

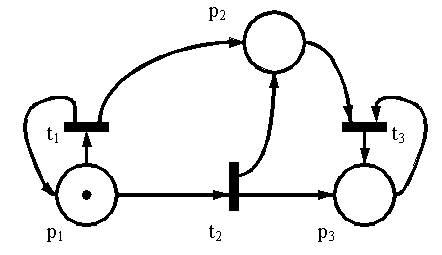
Ее начальная маркировка — (1, 0, 0). В этой начальной маркировке разрешены t 1 и t 2 . Чтобы рассмотреть все множество достижимости, определим новые вершины в дереве достижимости для других достижимых маркировок, получающихся в результате запуска каждого из этих двух переходов. Начальной (корневой) является вершина, соответствующая начальной маркировке. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рисунок 2).

Рис.2. Первый шаг построения дерева достижимости

Это частичное дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.

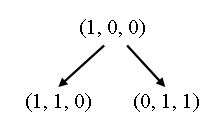
Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1, 1, 0) можно снова запустить t 1 (получая 1, 2, 0) и t 2 (получая (0, 2, 1)); из (0, 1, 1) можно запустить t 3 (получая 0, 0, 1). Это порождает дерево, изображенное на рисунке 3.

Рис.3. Второй шаг построения дерева достижимости

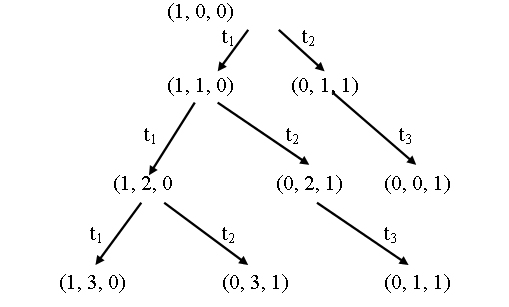
Начиная с трех новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево, как показано на рисунке 4.

Рис.4. Третий шаг построения дерева достижимости

Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешенным, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут. Кроме того, необходимо отметить, что маркировка (0,1, 1), порождаемая запуском t 3 в (0, 2, 1) была уже порождена непосредственно из начальной маркировки запуском t 2 .

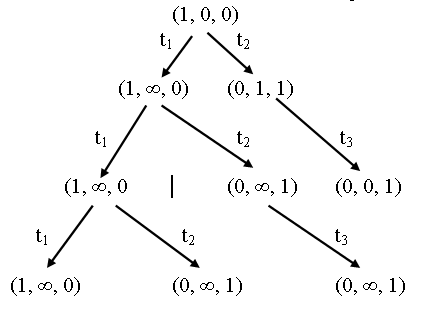
Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порожденной. Однако получившееся дерево достижимости может оказаться бесконечным, так как будет порождена каждая маркировка из множества достижимости. Поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рисунок 5).

Рис.5. Простая сеть Петри с бесконечным деревом достижимости

Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов.

Для получения дерева, которое можно считать полезным инструментом анализа необходимо найти средства ограничения его до конечного размера. Отметим, что если какое-то представление бесконечного множества конечно, то бесконечное множество маркировок должно отображаться в такое представление. В общем случае это приведет к потере информации и, возможно, к тому, что некоторые свойства сетей Петри определить будет нельзя, но все зависит от того, как представление было получено.

Приведение к конечному представлению осуществляется несколькими способами. Прежде всего, необходимо использовать те средства, которые ограничивают введение новых маркировок (называемых граничными вершинами) на каждом шаге. Для этого могут вводиться пассивные маркировки, то есть маркировки, в которых нет разрешенных переходов. Такие пассивные маркировки называются терминальными вершинами . Другой класс маркировок — это маркировки, ранее встречавшиеся в дереве. Такие маркировки называются дублирующими вершинами : никакие последующие маркировки можно не рассматривать — все они будут порождены из места первого появления дублирующей маркировки в дереве. Таким образом, в дереве на рисунке 5 маркировка (0, 1, 1), получившаяся в результате выполнения последовательности t 1 , t 2 , t 3 , не будет порождать какие-либо новые вершины в дереве, поскольку она ранее встречалась в дереве в результате выполнения последовательности t 2 из начальной маркировки.

Каждая вершина может классифицироваться как граничная вершина, терминальная вершина, дублирующая вершина или как внутренняя вершина. Граничными являются вершины, еще не обработанные алгоритмом, а после обработки они могут стать терминальными, дублирующими или внутренними вершинами.

Алгоритм обычно начинается с определения начальной маркировки корнем дерева, т. е. граничной вершиной.

если в дереве имеется другая вершина у , не являющаяся граничной, и с ней связана та же маркировка, m(х) = m(у) , то вершина х — дублирующая;
если для маркировки m(х) ни один из переходов не разрешен, то х — терминальная вершина;
дуга, помеченная t j , направлена от вершины х к вершине у . Вершина х переопределяется как внутренняя, вершина у — становится граничной.

Если все вершины дерева — терминальные, дублирующие или внутренние, то обработка данным алгоритмом останавливается. Определение. Задача покрываемости. Для заданной сети Петри С с начальной маркировкой m и маркировки m’ определить, существует ли такая достижимая маркировка m» принадлежащая R(C, m) , что m» >= m . Маркировка m» покрывает m’ .

Это требование можно усложнить, если определять достижимость и покрываемость для множества маркировок, тогда можно перейти к задачам достижимости множества и покрываемости множества. Однако, если множество конечно, то такие задачи можно решить обычным многократным решением соответствующих задач достижимости и покрываемости для одной маркировки.

Дружинин В. А. Использование сетей Петри для моделирования технологических процессов / Дружинин В. А., Борде Т. Д. // Радиоэлектроника, информатика, управление. — 1999. — №2. — С. 65-72.
Захаров Н. Г. Синтез цифровых автоматов. Учебное пособие / Захаров Н. Г., Рогов В. Н. / Ульяновский гос. техн. ун-т. — Ульяновск, 2003. — 135 с.
Кирюшин О.В. Анализ систем с помощью сетей Петри. Учебно-методическое пособие / Кирюшин О.В. / Уфимский гос. нефт. техн. ун-т. — Уфа, 2006. — 18 с.
Котов В.Е. Сети Петри: Пер. с англ. / Котов В.Е. — М.: Наука, 1984. — 160 с.
Лескин А.А. Сети Петри в моделировании и управлении / Лескин А. А., Мальцев П. А., Спиридонов А. М. — Л.: Наука, 1989. — 133 с.
Никулина Н. О. Применение аппарата сетей Петри для моделирования экономических процессов. Методические указания к лабораторным работам по курсу «ЛВС и распределенная обработка данных в банках» / Никулина Н. О., Старцева Е. Б. / Уфимский гос. авиац. техн. ун-т. — Уфа, 2001. — 32 с.
Павлова А. В. Математические основы теории систем. Учебное пособие / Павлова Н. О. /Белорусский гос. ун-т информатики и радиоэлектроники. — Минск, 2004. — 84 с.
Питерсон Дж. Теория сетей Петри и моделирование систем / Питерсон Дж. — М.: Мир, 1984. — 264 с.
Федотов И. Е. Некоторые приемы параллельного программирования. Учебное пособие. / Московский гос. ин-т радиоэлектроники, электроники и автоматики. — Москва, 2008. — 188 с.
Сети Петри. Моделирование с помощью сетей Петри [Электронный ресурс] http://www.modelling-process.ru
Моделирование (базовый курс) [Электронный ресурс] http://bigor.bmstu.ru
Теория информационных технологий и систем. Лекция: Сети Петри [Электронный ресурс] http://www.intuit.ru
Моделирование информационных процессов и систем [Электронный ресурс] http://www.best-in-web.narod.ru

Удачи в освоении и использовании сетей Петри!

Источник

10.10. Дерево достижимости сети Петри

Основным методом анализа сетей Петри является построение дерева достижимости, позволяющий найти множество маркировок, достижимых из заданной начальной маркировки сети Петри.

Построение дерева достижимости легко выполняется путем счета по компьютерной программе, написанной для данного варианта сети.

Рассмотрим процесс построения дерева достижимости на конкретном примере.

Рис. 10.21. Сеть Петри, для которой строится дерево достижимости.

Начальная маркировка сети μ₀ = (1, 0, 0) – фишка находится в позиции p₁. В этот момент разрешены два перехода: t₁ и t₂. Дерево достижимости должно охватывать все возможные варианты эволюции сети. В результате срабатывания перехода t₁ будет достигнута маркировка μ₁ = (1, 1, 0), а в результате срабатывания перехода t₂ — маркировка μ₂ = (0, 1, 1). Фрагмент дерева достижимости для первого шага имеет следующий вид:

Из маркировки μ₁ = (1, 1, 0) можно запустить переход t₁ и получить маркировку μ₃ = (1, 2, 0).и запустить переход t₂ и получить переход μ₄ = (0, 2, 1). Из маркировки μ₂ = (0, 1, 1) можно запустить переход и получить маркировку μ₅ = (0, 0, 1). В результате получим

дерево достижимости для второго шага построения.

Для третьего шага получим

Продолжая таким образом заметим, что в результате для конечной сети Петри строится бесконечное дерево достижимости. Приведение такого дерева к конечному виду проводится следующим способом. Введение новых маркировок ограничивается на каждом шаге граничными вершинами. Это:

пассивные маркировки, из которых никакие переходы невозможны (такой является маркировка μ₅ = (0, 0, 1), полученная в результате срабатывания переходов t₂ t₃, и
ранее встречавшиеся маркировки, из которых повторяются уже построенные фрагменты дерева достижимости. Такой является маркировка μ₂ = (0, 1, 1), полученная в результате срабатывания последовательности переходов t₁ t₂ t₃ .

Для этого дерева только маркировка μ₅ = (0, 0, 1) является пассивной. Для всех остальных маркировок некоторые переходы сети оказываются разрешенными, что приводит к постепенному накоплению фишек в позиции p₂. Это означает, что сеть имеет бесконечное множество маркировок, что отмечено на конечном дереве достижимости для этой сети.

Если последовательность маркировок ограничена (символ ∞ отсутствует в дереве достижимости), то число состояний сети Петри конечно. Дерево достижимости является графом состояний для этой сети. В этом практически важном случае находить множество всех достижимых маркировок (множество состояний сети) можно простым перебором. Понятно, что только ограниченная сеть Петри является безопасной, в которой число фишек в позициях не может превышать некоторое конечное число. Такая сеть аппаратно осуществима. Пример ограниченной сети Петри приведен на следующем рисунке.

Рис. 10.22. Ограниченная сеть Петри

Дерево достижимости для этой сети имеет следующий вид:

Граф достижимости показывает, что сеть Петри ограничена и безопасна. Дерево достижимости позволяет легко проверить, является ли сеть сохраняющей или нет. Для этого достаточно сложить количество фишек для каждой маркировки (для каждой вершины дерева достижимости) и сравнить суммы. Если они одинаковы, то сеть сохраняющая. Сеть на рис. 10.22 не является сохраняющей.

Анализ дерева достижимости для ограниченной сети Петри позволяет определить все его свойства, перечисленные выше. Если сеть неограниченна (в разметке дерева достижимости присутствует символ ∞), то анализ сети затруднен. Наличие символа ∞ означает потерю части информации о свойствах сети.

Основным недостатком сетей Петри являются трудности моделирования времени работы (времени задержки) переходов. Поэтому классические сети Петри позволяют эффективно моделировать логику работы программ и технических устройств, но имитационное моделирование временных характеристик в них затруднено. Поэтому разработаны различные варианты расширения возможностей сетей Петри, приспособленных к решению различных конкретных задач.

10.11. Е – сеть

Наиболее современным и продвинутым к задачам графического программирования и моделирования вычислительных систем являются Е–сети (от английского evaluation – вычисления).

Е-сети включают несколько типов позиций:

Меткам (фишкам) в Е-сети могут присваиваться атрибуты.

Переходам приписывается время задержки и функции преобразования атрибутов меток.

Источник