Действительно ли пустые Деревья двоичного поиска допустимы?
Как уже указывалось, Lua использует ключевое слово not для логической инверсии, а не оператор ! . Выложенный вами код выглядит как gLua: вариант Lua, основанный на Lua 5.1 и разработанный для Garry’s Mod. Среди отличий от чистого Lua 5.1 он реализует множество операторов в стиле C, как указано здесь здесь . Попытка запустить gLua в обычной среде Lua не будет работать, так как базовая Lua не поддерживает эти операторы, а некоторые встроенные функции Lua ведут себя по-разному в gLua.
РЕДАКТИРОВАТЬ: Если выполняется в среде gLua, причиной проблемы, вероятно, является использование entity.GetrHealth : это не базовая функция, вы намеревались entity.GetHealth ?
5 ответов
Точное значение пустого дерева, конечно же, зависит от вашей реализации, равно как и значение слова «действительный», но в целом я бы сказал «да» на оба вопроса. Пустое дерево представляет случай, когда набор сущностей, в который вы вставили, пуст, а единственный узел — случай, когда набор содержит одну сущность.
Один узел без дочерних элементов, безусловно, действителен и согласно Структура двоичного дерева :
- Когда оно пустое, оно не содержит данных.
- Когда он не пустой, он содержит объект данных, называемый корневым элементом, и 2 различных объекта BiTree, называемых левым поддеревом и правым поддеревом.
Для полноты, эта запись в Википедии является довольно полезное краткое изложение терминологии и тому подобное.
Допустимо ли пустое дерево (нулевое)?
Если его пусто, дерева нет. Следовательно, вопрос о действительности не возникает.
Является ли действительным корневой узел без дочерних элементов?
Да. Это тройник с одним элементом.
Я думаю, что вы смешиваете яблоки и апельсины:
- null — это значение в некоторых языках программирования, и оно связано с конкретным представлением вашей реализации структуры данных
- «Пусто» — это свойство абстрактной структуры данных, которую мы называем «бинарное дерево поиска»
Теперь дерево — это упорядоченный набор: ни больше, ни меньше. Конечно, набор может быть пустым! Это означает, что в вашей реализации что-то похожее на:
представляет пустое дерево? Ну, это зависит от вашей модели. Например, вы можете подумать, что пустое поддерево должно быть представлено узлом без значения и с аннулированными ссылками на листья: в этой модели нулевой указатель не имеет смысла с логической точки зрения. Но это только один подход! Подход, основанный на дозорных, — это удовольствие для программирования, но он требует большого объема памяти: тогда вы можете моделировать пустые узлы только с нулем. В этом случае указатель null может быть пустым деревом.
Источник
2. Двоичные деревья
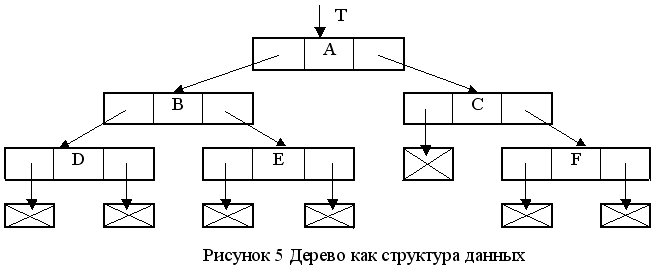
Особенно важную роль играют упорядоченные деревья второй степени. Их называют двоичными или бинарными деревьями. Определим двоичное дерево как конечное множество элементов – узлов, которое или пусто, или состоит из корня и двух непересекающихся двоичных деревьев, называемых левым и правым поддеревьями данного корня. Заметим, что двоичное дерево не является частным случаем дерева, хотя эти два понятия связаны между собой. Основные отличия между ними: 1) Дерево никогда не бывает пустым, т.е. имеет, по меньшей мере, один узел, а двоичное дерево может быть пустым. 2) Двоичное дерево — упорядоченное дерево, т.е. делается различие между левым и правым поддеревом, даже в том случае, когда узел имеет лишь одного потомка. В графическом изображении дерева (рисунок 4) “наклон” ветвей важен. Реализация таких рекурсивных структур, как двоичные деревья, приводит к использованию ссылок (указателей). Ссылки на пустые деревья будут обозначаться nil. Из определения двоичных деревьев следует естественный способ их описания ( и представления в компьютере ) : для этого достаточно иметь две связи L и R в каждом узле и переменную связи T, которая является указателем на это дерево. Если дерево пусто, то T = nil ; в противном случае T — адрес корня этого дерева, а L и R — указатели соответственно на левое и правое поддеревья этого корня. На языке Паскаль узлы бинарного дерева описываются как записи с одним или несколькими информационными полями и двумя полями – указателями. Если Elem — тип информационной части узлов дерева, то компоненты дерева ( узел и ссылка на узел ) имеют такие типы: type Tree = ^Node; < указатель на узел >Node = record < узел дерева >
Inf : Elem;
L, R : Tree end; Таким образом, дерево на рисунке 4 б) можно представить так, как на рисунке 5. Далее будем иметь дело только с двоичными деревьями, поэтому термин “дерево” будет означать двоичное дерево.
3. Основные операции с двоичными деревьями
3.1. Обход дерева Наиболее распространенная задача обработки древовидных структур – выполнение некоторой определенной операции над каждым элементом дерева. При этом происходит “посещение” всех вершин, т.е. обход дерева. При обходе каждый узел проходится, по меньшей мере, один раз, а, вообще говоря, три раза. Полное прохождение дерева дает линейную расстановку узлов. Если, обходя дерево, обрабатывать вершины при первой встрече, то ( см. рис. 4 б) ) получим последовательность A, B, D, E, C, F ; если при второй встрече, то получим D, B, E, A, C, F ; если при третьей встрече, то получим D, E, B, F, C, A. Эти три способа обхода называются соответственно – обходом сверху вниз (в прямом порядке, префиксным обходом, preorder); – обходом слева направо (в обратном порядке, инфиксным обходом, inorder); – обходом снизу вверх (в концевом порядке, постфиксным обходом, postorder или endorder). Способы прохождения деревьев определяются рекурсивно. Если дерево пусто, то никаких действий не выполняется, в противном случае обход выполняется в три этапа
| Префиксный обход | Инфиксный обход |
| Обработать узел | Пройти левое поддерево |
| Пройти левое поддерево | Обработать узел |
| Пройти правое поддерево | Пройти правое поддерево |
Постфиксный обход Пройти левое поддерево Пройти правое поддерево Обработать узел Обход слева направо (инфиксный обход) часто используется при сортировке (см. раздел 4 ). Префиксный и постфиксный способы обхода дерева играют важную роль при анализе текстов на языках программирования. Все три метода легко представляются как рекурсивные процедуры. Пример 3.1. Префиксный обход дерева : procedure PreOrder(T : Tree); begin if T <> nil then begin < операция обработки узла дерева , например, writeln( T^.inf );> PreOrder (T^.L); PreOrder (T^.R) end end; PreOrder > Пример 3.2. Инфиксный обход дерева : procedure InOrder(T : Tree); begin if T <> nil then begin InOrder (T^.L); < операция обработки узла дерева , например, writeln( T^.inf );> InOrder (T^.R) end end; Пример 3.3. Постфиксный обход дерева : procedure PostOrder(T : Tree); begin if T <> nil then begin PostOrder (T^.L); PostOrder (T^.R) < операция обработки узла дерева , например, writeln( T^.inf );> end end; PostOrder > Замечание. Ссылка T передается как параметр — значение, т.е. в процедуре используется ее локальная копия. При реализации нерекурсивных процедур обхода дерева обычно используют вспомогательный стек и операции работы с ним: – очистить стек (создать пустой стек); – проверить, является ли стек пустым; – добавить в стек элемент; – извлечь элемент из стека. В стеке запоминаются ссылки на вершины (поддеревья), обработка которых временно откладывается. Пример 3.4. Описать нерекурсивную процедуру префиксного обхода дерева. Описание вспомогательного стека : type Stack = ^Rec; Rec = record
Источник
1.3.4. Деревья и их представление
Конечное корневоедерево T формально определяется как непустое множество упорядоченных узлов, таких что существует один выделенный узел, называемыйкорнемдерева, а оставшиеся узлы разбиты на m>=0 поддеревьев Т1,Т2. Тm. Узлы, не имеющие поддеревьев, называютсялистьями; остальные узлы называются внутренними узлами.
Рис.3.8. Дерево с 11 узлами, помеченными буквами от А до К. Узлы с метками D,E,F,H,J и K являются листьями; другие узлы внутренние. Узел А — корень.
Посредством деревьев изображаются иерархические организации, поэтому они являются нелинейными структурами данных в комбинаторных алгоритмах.
В описанных соотношениях между узлами дерева мы используем терминологию, принятую в генеалогических деревьях. Так, мы говорим, что в дереве (или поддереве) все узлы являются потомками его корня, и наоборот, корень — предок всех своих потомков. Корень именуется отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. Например, на рис. 3.8 узел А является отцом узлов B,G и I; J и K — сыновья I, а C, E, F -братья.
Все рассматриваемые нами деревья будут упорядочены, т.е. для них будет важен относительный порядок расположения каждого узла. Таким образом, деревья считаются различными.
Определим лес как упорядоченное множество деревьев; в связи с этим мы можем перефразировать определение дерева: дерево есть непустое множество узлов, такое, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы образуют лес с m>=0 поддеревьями корня.
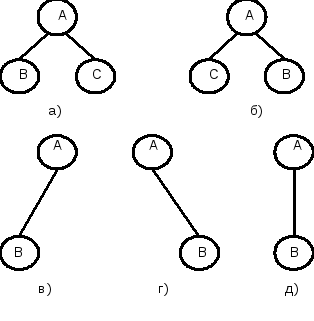
Важной разновидностью корневых деревьев является класс бинарных деревьев. Бинарное дерево Т либо пустое, либо состоит из выделенного узла, называемого корнем, и двух бинарных поддеревьев: левого Тlи правого Tr. Бинарные деревья, вообще говоря не являются подмножеством множества деревьев, они полностью отличаются по своей структуре, поскольку две следующие картинки ( а) и б)) не изображают одно и то же бинарное дерево. Как деревья, однако, они обе неотличимы от ( в) ).
Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, и каждый узел дерева может иметь произвольное число поддеревьев; в тоже время бинарное дерево может быть пустым, каждая из его вершин может иметь 0, 1 или 2 поддерева, и существует различие между левыми и правыми поддеревьями.
Почти все машинное представления деревьев основаны на связанных распределениях. Каждый узел состоит из поля INFO и некоторых полей для указателей. Например, одно из представлений для каждого узла имеет единственное поле для указателя F (FATHER), указывающее на отца данного узла. При этом приведенное на рис.3.8 дерево будет выглядеть так, как показано на рис.310.
Рис.3.10.Дерево из рис.3.8, представленное из узлов с полем INFO и указателем FATHER.
Такое представление полезно, если необходимо подниматься по дереву от потомков к предкам. Такая операция встречается довольно редко; чаще требуется опуститься по дереву от предков к потомкам.
Представление дерева (или леса) с использованием указателей, ведущих от предков к потомкам, довольно сложно, поскольку узел, имея не более одного отца, может иметь в тоже время произвольно много сыновей. Другими словами, при таком представлении узлы должны различаться по размеру, что является определенным неудобством. Один из путей обхода этой трудности состоит в том, чтобы определить соотношение между деревьями и бинарными деревьями, поскольку бинарные деревья легко представить узлами фиксированного размера. Каждый узел в этом случае имеет три поля: LEFT (указывает положение корня левого поддерева), INFO (содержимое узла) и RIGHT (указатель местоположения корня правого поддерева). Все сказанное выше проиллюстри-ровано на рис.3.11.
а) б)
Рис.3.11. Бинарное дерево (а) и его представление (б) с помощью узлов с тремя
полями LEFT , INFO и RIGTH.
Мы можем представлять деревья как бинарные деревья ( используя узлы фиксированного размера), представляя каждый узел леса в виде узла, состоящего из полей LEFT, INFO и RIGHT. При этом поле LEFT предназначается для указания самого левого сына
данного узла, а поле RIGHT — для указания следующего брата данного узла. Например, лес (рис.3.11,а) преобразуется в бинарное дерево ( рис.3.11,б). Таким образом, мы используем поле LEFT некоторого узла для указателя на связанный список сыновей этого узла; этот список связывается с помощью полей RIGHT. Такое представление мы будем называть естественным соответствием между лесами и бинарными деревьями.
а)
Рис.3.12. Лес (а) и его представление в виде бинарного дерева (б)
Двоичное дерево обычно представляют в виде двух массивов LES (LEFTSON-левый сын) и RIS (RIGHTSON-правый сын). Пусть узлы двоичного дерева занумерованы целыми числами от 1 до N. В этом случае LES[i]=j узел с номером j является левым сыном узла с номером i. Если у узла i нет левого сына, то LES[i]=0. RES[i] определяется аналогично.
Источник