- LCA — lowest (least) common ancestor Наименьший общий предок двух вершин
- Наивная реализация
- Метод двоичных подъёмов
- А как еще можно?
- А ещё?
- ВАЖНО!
- Найдите наименьшего общего предка (LCA) двух узлов в двоичном дереве
- Сведение задачи LCA к задаче RMQ
- Препроцессинг
- Запрос
- Доказательство корректности алгоритма
- Пример
- Сложность
- См.также
- Источники информации
LCA — lowest (least) common ancestor
Наименьший общий предок двух вершин
Для начала давайте разберемся, что такое общий предок двух вершин \(u\) и \(v\).
Это любая такая вершина \(t\), которая лежит на пути от корня до \(u\) и на пути от корня до \(v\).
Тогда наименьшим общим предком \(u\) и \(v\) назовем такую вершину \(t\), которая является их общим предком, и расстояние от корня до нее максимально.
Зачем нужно уметь его искать?
В последнее время я все реже встречаю задачи, требующие именно явного нахождения наименьшего общего предка, но порой попадаются задачи про запросы на пути, а с ними нам может помочь LCA.
Наивная реализация
Для начала рассмотрим самую простую реализацию поиска LCA:
vector> gr; \\ наш граф vector pre; \\ массив предков vector d; \\ массив глубин void dfs(int v, int p = -1) < if (p == -1) d[v] = 0; else d[v] = d[p] + 1; pre[v] = p; for (int to : gr[v]) if (to != p) dfs(to, v); >int getLCA(int a, int b) < while (a != b) < if (d[a] >d[b]) a = pre[a]; else b = pre[b]; > return a; > int main() < . // считываем граф dfs(root) // запускаем дфс от корня for () < . // считываем запрос getLCA(a, b); // отвечаем на него >> Давайте посмотрим, что делает наш алгоритм. Пусть сейчас выбраны вершины \(a\) и \(b\).
Их LCA имеет глубину не больше, чем минимум из глубин \(a\) и \(b\), так как лежит на пути от корня до этих вершин.
Значит, если глубины вершин неравны, то можно смело заменять более глубокую вершину ее предком.
Теперь допустим, что глубины вершин одинаковы.
Тогда если они равны, то очевидно что это и есть LCA.
Иначе, LCA имеет губину меньшую, чем та, на которой сейчас расположены вершины, и опять можно заменить их своими предками.
Отлично, теперь давайте оценим время работы.
dfs() отработает за O(n)
getLCA() в худшем случае будет работать за O(n) (например, если граф — бамбук, и мы спрашиваем ответ от его концов)
Таким образом, алгоритм работает за O(q * n) — достаточно долго.
Здесь и далее \(n\) — число вершин в графе, а \(q\) — количество запросов
Давайте попробуем ускорить наш алгоритм.
Метод двоичных подъёмов
Если очень внимательно посмотреть на предыдущую реализацию, то можно заметить два этапа в ней:
Первый — глубина вершин выравнивается.
Второй — вершины параллельно поднимаются наверх, пока не станут равными.
Тогда давайте ходить не по 1, а большими блоками. Например, степенями двойки.
Для начала разберемся, как их предпосчитать.
vector> gr; vector d; vector> bl; // бинарные подъемы // этот массив следует инициализировать так: bl[log(n)+1][n] // log(n)+1 ассив по n элементов void dfs(int v, int p = -1) < if (p == -1) < p = v; d[v] = 0; >else d[v] = d[p] + 1; bl[0][v] = p; for (int i = 1; i
Почему это работает? В цикле построения bl мы говорим, что подняться на \(2^i\) то же самое, что подняться на \(2^\) два раза.
Как можно заметить, в такой реализации нельзя подняться выше корня, а значит, не нужны дополнительные if.
Как же тут отвечать на запрос? Давайте разбираться.
int getLCA(int a, int b) < if (d[a] >d[b]) swap(a, b); // Теперь b глубже a for (int i = bl.size() - 1; i >= 0; --i) if (d[bl[i][b]] >= d[a]) b = bl[i][b]; // Теперь их глубины равны if (a == b) return a; // Если они равны, то это и есть LCA for (int i = bl.size() - 1; i >= 0; --i) if (bl[i][b] != bl[i][a]) < a = bl[i][a]; b = bl[i][b]; >//Теперь верно, что a != b и их глубина минимальна return bl[0][a]; > Теперь есть два варианта:
Первый — вы верите мне, что это работает. Тогда делайте *ТЫК* и читайте дальше
Второй — вы хотите понять, что вообще произошло. Тогда продолжайте читать дальше.
Для начала докажем, что работает первый этап и глубина b становится равной глубине a.
Рассмотрим число \(x = (d[b] — d[a])\),
тогда когда мы пойдем от меньшего бита к большему, мы будем совершать переход только тогда, когда этот бит есть в числе.
Почему? Потому что если степень двойки больше, чем максимальный бит числа, то эта степень точно больше самого числа.
Значит, мы будем всегда совершать переход по самому большому биту числа.
После этого расстояние уменьшится на эту степень двойки, и мы перейдем к меньшему расстоянию, с которым по аналогии возьмем переход в соответствии с максимальным битом. Кстати, на этом можно основать некоторую оптимизацию. Вместо цикла
for (int i = bl.size() - 1; i >= 0; --i) if (d[bl[i][b]] >= d[a]) b = bl[i][b]; int x = d[b] - d[a]; for (int i = bl.size() - 1; i >= 0; --i) if (x & (1 А что происходит на втором этапе?
Вообще, мы хотим максимально подняться так, чтобы a было все еще не было равно b.
Значит, есть какая-то глубина x, на которую нам хотелось бы подняться, но мы ее не знаем. У нас есть условие \(a \neq b\), которое мы и будем использовать.
Опять таки, мы не можем перейти по биту больше, чем максимальный, а по максимальному можем всегда. Так мы поднимемся максимально и сохраним \(a\neq b\), а значит, их предок уже таков, что \(pre[a] = pre[b]\), следовательно, это и есть LCA.
Что еще умеют бинподъемы?
Например, можно посчитать какую-то функцию на пути, параллельно с поиском LCA.
Для этого давайте хранить bl как массив пар вида \( [to, f] \) - куда нужно перейти, и какое значение функции на этом переходе.
Покажу на примере минимума. Он хорош тем, что нельзя брать его на пути до корня, а потом вычитать ответ на пути от LCA до корня.
Например, сумму можно считать так: если \(sum[v]\) - сумма на пути до вершины v, то сумма на пути от a до b считается как \(sum[a] + sum[b] - 2 * sum[LCA]\). Это если значения записаны на ребрах.
С минимумом так не выйдет.
vector>> gr; vector d; vector>> bl; void dfs(int v, int p = -1, int pEdge = inf) < if (p == -1) < p = v; d[v] = 0; >else d[v] = d[p] + 1; bl[0][v] = ; for (int i = 1; i < bl.size(); ++i) bl[i][v] = to : gr[v]) dfs(to.first, v, to.second); > int getMIN(int a, int b) < int ans = inf; if (d[a] >d[b]) swap(a, b); for (int i = bl.size() - 1; i >= 0; --i) if (d[bl[i][b].first] >= d[a]) < ans = min(ans, bl[i][b].second); b = bl[i][b].first; >if (a == b) return ans; for (int i = bl.size() - 1; i >= 0; --i) if (bl[i][b].first != bl[i][a].first) < ans = min(ans, bl[i][b].second); ans = min(ans, bl[i][a].second); a = bl[i][a].first; b = bl[i][b].first; >ans = min(); return ans; > Ну и самое важное: время и память!
Как можно заметить, алгоритм требует \(O(n \cdot log(n))\) памяти и \(O(n \cdot log(n))\) времени на предподсчет
Но вот ответ на запрос занимает всего \(O(log(n))\)
Получаем \(O(n \cdot log(n) + q \cdot log(n))\)
А как еще можно?
Можно свести LCA к RMQ и решать его любыми удобными вам методами - ДО, Sparse-table.
Как свести? Давайте выпишем Эйлеров обход графа. Тогда ответом будет вершина на полуинтервале \([min(first[a], first[b]), max(last[a], last[b]))\), глубина которой минимальна.
Здесть first и last - массивы первых и последних вхождений вершины в Эйлеров обход.
vector> gr; vector d; vector> euler; vector first; vector last; void dfs(int v, int p = -1) < if (p == -1) d[v] = 0; else d[v] = d[p] + 1; first[v] = euler.size(); euler.push_back(); for (int to : gr[v]) < dfs(to, v); euler.push_back(); > last[v] = euler.size(); > Теперь можно взять первый элемент и минимум по вторым элементам пар на полуинтервале, это и будет LCA.
Почему так? Эйлеров обход записывает вершину в самом начале и после обхода каждого поддерева. То есть, если минимум на отрезке - какая-то вершина v, то две данные находятся в разных ее поддеревьях.
Какие плюсы и минусы?
К плюсам можно отнести то, что используя столько же памяти, сколько бинарные подъемы, можно построить sparse-table и отвечать на запросы за O(1).
А также, что можно использовать O(n) памяти, например - ДО.
Минусы - нельзя вычислять что-то на пути (только если это не Мо. Но это лучше даже в голову не брать.)
А ещё?
Есть алгоритм, требующий \(O(n)\) как памяти, так и времени на предподсчет. Отвечает на запрос он за \(O(1)\).
Но рассказывать его я не буду (пока уж точно), так как он мало применим на практике и будет бесполезен на олимпиадах.
ВАЖНО!
Все алгоритмы, описанные в данном тексте, умеют отвечать на запросы онлайн. Запрос пришел - мы ответили.
Бинарные подъемы умеют даже добавлять вершину в дерево. Для этого нужно просто представить, что мы пришли в нее в ходе дфс, и пройтись циклом по степеням двойки.
Если все запросы известны заранее, лучше использовать алгоритм Тарьяна. Про него я напишу отдельно.
Источник
Найдите наименьшего общего предка (LCA) двух узлов в двоичном дереве
Имея бинарное дерево и два узла, x а также y , найти наименьшего общего предка (LCA) x а также y в этом. Решение должно возвращать значение null, если либо x или же y не является фактическим узлом в дереве.
Наименьший общий предок (LCA) двух узлов x а также y в бинарном дереве — это самый нижний (т. е. самый глубокий) узел, который имеет оба x а также y как потомки, где каждый узел может быть потомком самого себя (поэтому, если x доступен из w , w является LCA). Другими словами, LCA x а также y является общим предком x а также y который находится дальше всего от корня.
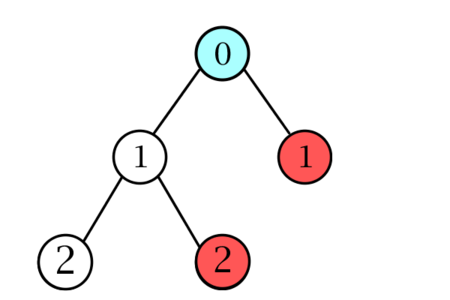
Например, рассмотрим следующее бинарное дерево. Позволять x = 6 а также y = 7 . Общие предки узлов x а также y равны 1 и 3. Из узлов 1 и 3 LCA равен 3, поскольку он находится дальше всего от корня.

Простым решением было бы сохранить путь от корня к x и путь от корня к y в двух вспомогательных массивах. Затем просматривайте оба массива одновременно, пока значения в массивах не совпадут. Последнее совпадающее значение будет LCA. Если достигнут конец одного массива, то последним увиденным значением будет LCA. Временная сложность этого решения O(n) , куда n это общее количество узлов в бинарном дереве. Но используемое им вспомогательное пространство равно O(n) требуется для хранения двух массивов.
Мы можем рекурсивно найти наименьшего общего предка узлов x а также y присутствуют в бинарном дереве. Хитрость заключается в том, чтобы найти узел в двоичном дереве с одним ключом, присутствующим в его левом поддереве, и другим ключом, присутствующим в правом поддереве. Если какой-либо такой узел присутствует в дереве, то это LCA; если y лежит в поддереве с корнем в узле x , тогда x является ОЖЦ; иначе, если x лежит в поддереве с корнем в узле y , тогда y является ЛКА.
Алгоритм может быть реализован следующим образом на C++, Java и Python:
Источник
Сведение задачи LCA к задаче RMQ
Будем решать задачу [math]LCA[/math] , уже умея решать задачу [math]RMQ[/math] . Тогда поиск наименьшего общего предка [math]i[/math] -того и [math]j[/math] -того элементов сводится к запросу минимума на отрезке массива, который будет введен позднее.
Препроцессинг
Для каждой вершины [math]T[/math] определим глубину с помощью следующей рекурсивной формулы:
[math]\mathrm(u) = \begin 0 & u = \mathrm(T),\\ \mathrm(v) + 1 & u = \mathrm(v). \end[/math]
Ясно, что глубина вершины элементарным образом поддерживается во время обхода в глубину.
Запустим обход в глубину из корня, который будет вычислять значения следующих величин:
- Cписок глубин посещенных вершин [math]d[/math] . Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
- Список посещений узлов [math]\mathtt[/math] , строящийся аналогично предыдущему, только добавляется не глубина а сама вершина.
- Значение функции [math]\mathtt[u][/math] , возвращающей индекс в списке глубин [math]d[/math] , по которому была записана глубина вершины [math]u[/math] (например на момент входа в вершину).
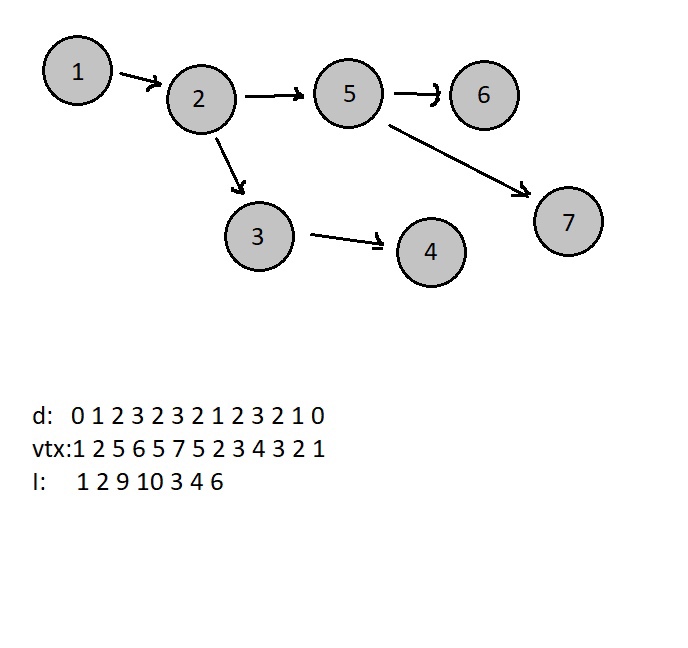
Вот таким образом будут выглядеть эти три массива после обхода в глубину:
Запрос
Будем считать, что [math]\mathrm(d,l,r)[/math] возвращает индекс минимального элемента в [math]d[/math] на отрезке [math][l..r][/math] . Тогда ответом на запрос [math]\mathrm(u, v)[/math] , где [math]\mathtt[u] \leqslant \mathtt[v][/math] , будет [math]\mathtt[\mathrm(d,\mathtt[u], \mathtt[v])][/math] .
Доказательство корректности алгоритма
Наименьшему общему предку вершин [math]u, v[/math] соответствует минимальная глубина на отрезке [math]d[\mathtt[u], \mathtt[v]][/math] .
Пример
Рассмотрим дерево на рисунке 1. Найдем наименьшего общего предка вершин, помеченных красным цветом. Список глубин, получающийся в результате обхода в глубину — [math][0, 1, 2, 1, 2, 1, 0, 1, 0].[/math] Глубина наименьшего общего предка красных вершин равна минимуму на отрезке [math][2, 1, 0, 1].[/math]
Сложность
Для нахождения минимального элемента на отрезке можно использовать алгоритм Фарака-Колтона и Бендера для [math]\pm 1RMQ[/math] , т. к. соседние элементы в списке глубин отличаются не более чем на единицу. Длина списка глубин составляет [math](2n - 1)[/math] , таким образом, препроцессинг работает за [math]O(n)[/math] . Время выполнения запроса равно времени запроса минимального элемента на отрезке — [math]O(1)[/math] .
См.также
Источники информации
Источник