Дерево обхода вершин графа

Обход в глубину, цвета вершин

Обход в глубину (поиск в глубину, англ. Depth-First Search, DFS) — один из основных методов обхода графа, часто используемый для проверки связности, поиска цикла и компонент сильной связности и для топологической сортировки.

Алгоритм

Общая идея

Общая идея алгоритма состоит в следующем: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.

Пошаговое представление

1. Выбираем любую вершину из еще не пройденных, обозначим ее как [math]u[/math] .
2. Запускаем процедуру [math]\mathrm[/math]
   • Помечаем вершину [math]u[/math] как пройденную
   • Для каждой не пройденной смежной с [math]u[/math] вершиной (назовем ее [math]v[/math] ) запускаем [math]\mathrm[/math]
3. Повторяем шаги 1 и 2, пока все вершины не окажутся пройденными.

Реализация

В массиве [math]\mathrm[/math] хранится информация о пройденных и не пройденных вершинах.

function doDfs(G[n]: Graph): // функция принимает граф G с количеством вершин n и выполняет обход в глубину во всем графе visited = array[n, false] // создаём массив посещённых вершины длины n, заполненный false изначально function dfs(u: int): visited[u] = true for v: (u, v) in G if not visited[v] dfs(v) for i = 1 to n if not visited[i] dfs(i)

Время работы

Оценим время работы обхода в глубину. Процедура [math]\mathrm[/math] вызывается от каждой вершины не более одного раза, а внутри процедуры рассматриваются все такие ребра [math]\ = u\>[/math] . Всего таких ребер для всех вершин в графе [math]O(E)[/math] , следовательно, время работы алгоритма оценивается как [math]O(V+E)[/math] .

Цвета вершин

Зачастую, простой информации «были/не были в вершине» не хватает для конкретных целей.

Поэтому в процессе алгоритма вершинам задают некоторые цвета:

• если вершина белая, значит, мы в ней еще не были, вершина не пройдена;
• серая — вершина проходится в текущей процедуре [math]\mathrm[/math] ;
• черная — вершина пройдена, все итерации [math]\mathrm[/math] от нее завершены.

Такие «метки» в основном используются при поиске цикла.

Реализация

Отличие реализации с цветами от предыдущей лишь в массиве [math]\mathrm[/math] , который мы назовем теперь [math]\mathrm[/math] . В нем будет хранится информация о цветах вершин.

function doDfs(G[n]: Graph): // функция принимает граф G с количеством вершин n и выполняет обход в глубину во всем графе color = array[n, white] function dfs(u: int): color[u] = gray for v: (u, v) in G if color[v] == white dfs(v) color[u] = black for i = 1 to n if color[i] == white dfs(i)

Пример

Рассмотрим, как будут изменяться цвета вершин при обходе в глубину данного графа.

Описание шага	Состояние графа
В функции [math]\mathrm[/math] присваиваем всем вершинам в массиве [math]\mathrm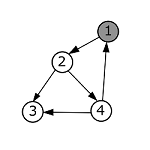[/math] белый цвет. Затем проверяем, что первая вершина окрашена в белый цвет. Заходим в нее и раскрашиваем ее в серый цвет.
Пробуем пойти в вершину с номером 2. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет.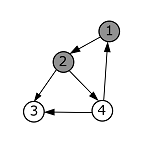
Пробуем пойти в вершину с номером 3. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет.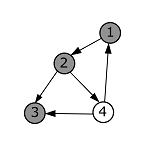
Проверяем, что из вершины с номером 3 не исходит ни одного ребра. Помечаем ее в черный цвет и возвращаемся в вершину с номером 2.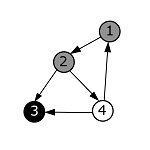
Пробуем пойти в вершину с номером 4. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет.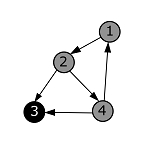
Пробуем пойти в вершину с номером 3. Видим, что она черного цвета, и остаемся на месте.
Пробуем пойти в вершину с номером 1. Видим, что она серого цвета, и остаемся на месте.
Из вершины с номером 4 больше нет исходящих ребер. Помечаем ее в черный цвет и возвращаемся в вершину с номером 2.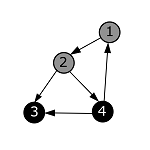
Из вершины с номером 2 больше нет исходящих ребер. Помечаем ее в черный цвет и возвращаемся в вершину с номером 1.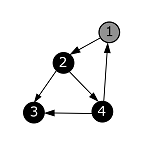
Из вершины с номером 1 больше нет исходящих ребер. Помечаем ее в черный цвет и выходим в программу [math]\mathrm[/math] . В ней проверяем, что все вершины окрашены в черный цвет. Выходим из функции [math]\mathrm[/math] . Алгоритм завершен.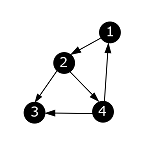

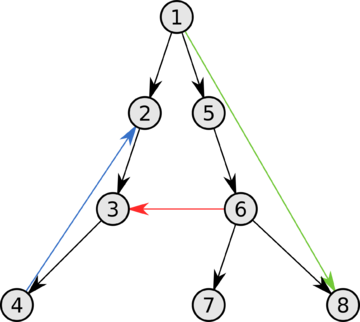
Дерево обхода в глубину

Типы ребер, определяемые деревом обхода:
1) ребра дерева
2) обратные ребра
3) прямые ребра
4) перекрестные ребра

Рассмотрим подграф предшествования обхода в глубину [math]G_p = (V, E_p)[/math] , где [math]E_p = \<(p[u], u) : u \in V,\ p[u] \neq NIL\>[/math] , где в свою очередь [math]p[u][/math] — вершина, от которой был вызван [math]\mathrm\ [/math] (для вершин, от которых [math]\mathrm[/math] был вызван нерекурсивно это значение соответственно равно [math]NIL[/math] ). Подграф предшествования поиска в глубину образует лес обхода в глубину, который состоит из нескольких деревьев обхода в глубину. С помощью полученного леса можно классифицировать ребра графа [math]G[/math] :

• Ребрами дерева назовем те ребра из [math]G[/math] , которые вошли в [math]G_p[/math] .
• Ребра [math](u, v)[/math] , соединяющие вершину [math]u[/math] с её предком [math]v[/math] в дереве обхода в глубину назовем обратными ребрами (для неориентированного графа предок должен быть не родителем, так как иначе ребро будет являться ребром дерева).
• Ребра [math](u, v)[/math] , не являющиеся ребрами дерева и соединяющие вершину [math]u[/math] с её потомком [math]v[/math] в дереве обхода в глубину назовем прямыми ребрами (в неориентированном графе нет разницы между прямыми и обратными ребрами, поэтому все такие ребра считаются обратными).
• Все остальные ребра назовем перекрестными ребрами — такие ребра могут соединять вершины одного и того же дерева обхода в глубину, когда ни одна из вершин не является предком другой, или соединять вершины в разных деревьях.

Алгоритм [math]\mathrm[/math] можно модифицировать так, что он будет классифицировать встречающиеся при работе ребра. Ключевая идея состоит в том, что каждое ребро [math](u, v)[/math] можно классифицировать при помощи цвета вершины [math]v[/math] при первом его исследовании, а именно:

• Белый цвет вершины [math]v[/math] по определению [math]\mathrm[/math] говорит о том, что это ребро дерева.
• Серый цвет в силу того, что серые вершины всегда образуют нисходящий путь в каком-либо из деревьев [math]\mathrm[/math] и встреченная вершина [math]v[/math] лежит на нем выше вершины [math]u[/math] , определяет обратное ребро (для неориентированного графа необходимо проверить условие [math]v \neq p[u][/math] ).
• Черный цвет, соответственно, указывает на прямое или перекрестное ребро.

См. также

Источники информации

• Википедия — Поиск в глубину
• Wikipedia — Depth-first search
• Обход в глубину. Реализации.
• Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, второе издание. Пер. с англ. — Издательский дом «Вильямс», 2007. — 1296 с. — Глава 22. Элементарные алгоритмы для работы с графами.

Источник

Реализуем алгоритм поиска в глубину

В этом туториале описан алгоритм поиска в глубину (depth first search, DFS) с псевдокодом и примерами. Кроме того, расписаны способы реализации поиска в глубину в C, Java, Python и C++.

“Поиск в глубину” или “обход в глубину” — это рекурсивный алгоритм по поиску всех вершин графа или дерева. Обход подразумевает под собой посещение всех вершин графа.

Алгоритм поиска в глубину

Стандартная реализация поиска в глубину помещает каждую вершину (узел, node) графа в одну из двух категорий:

Цель алгоритма состоит в том, чтобы пометить каждую вершину как “Пройденная”, избегая при этом циклов.

Алгоритм поиска в глубину работает следующим образом:

1. Начните с того, что поместите любую вершину графа на вершину стека.
2. Возьмите верхний элемент стека и добавьте его в список “Пройденных”.
3. Создайте список смежных вершин для этой вершины. Добавьте те вершины, которых нет в списке “Пройденных”, в верх стека.
4. Необходимо повторять шаги 2 и 3, пока стек не станет пустым.

Пример реализации поиска в глубину

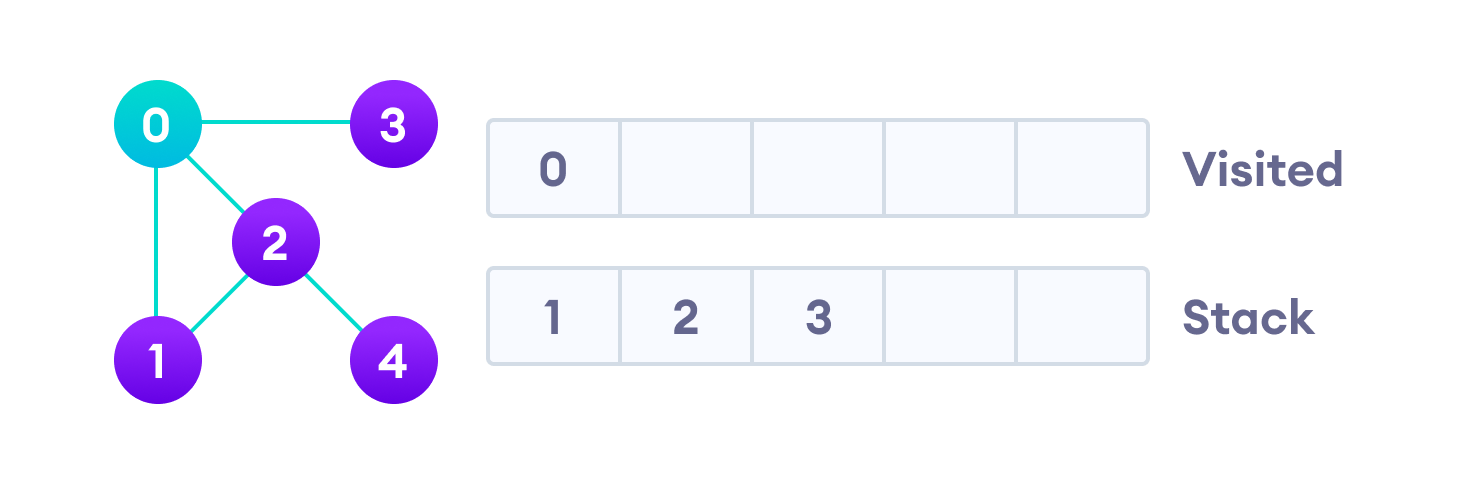
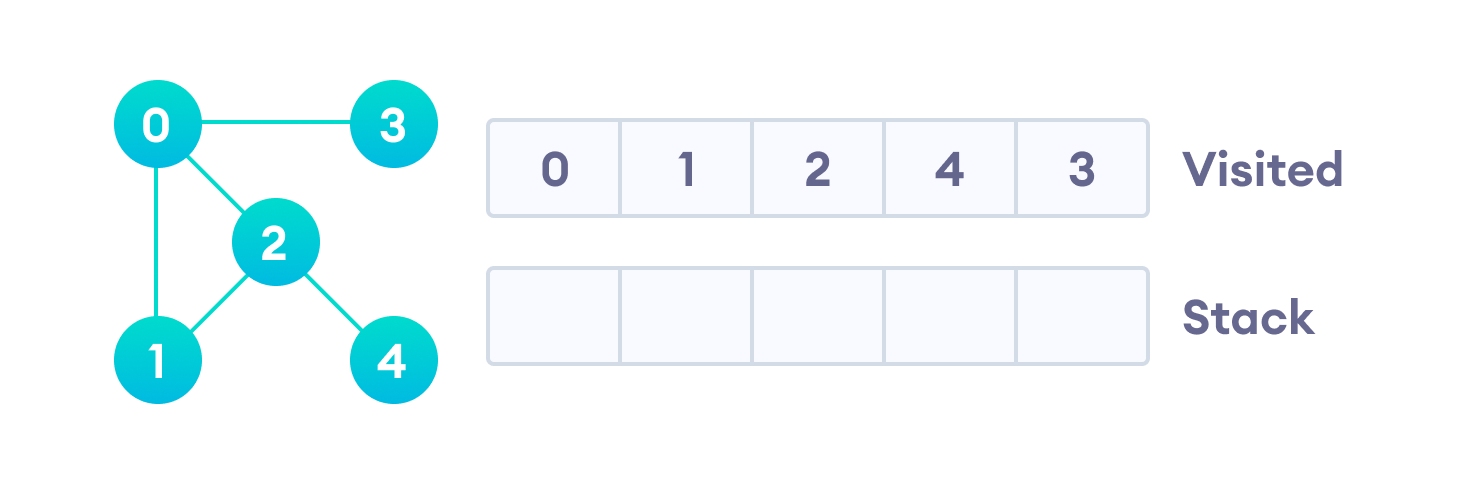
Предлагаю рассмотреть на примере, как работает алгоритм поиска в глубину. Мы будем использовать неориентированный граф с пятью вершинами.

Начнем мы с вершины “0”. В первую очередь алгоритм поиска в глубину поместит ее саму в список “Пройденные” (на изображении “Visited”), а ее смежные вершины — в стек.

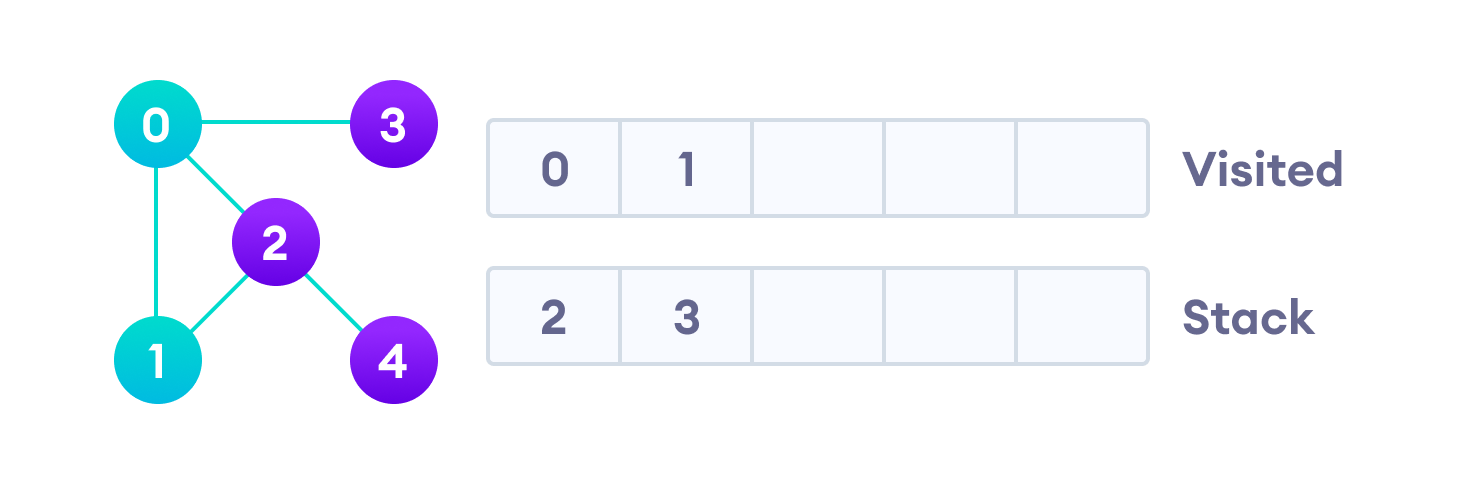
Затем мы берем следующий элемент сверху стека, т.е. к вершину “1”, и переходим к ее соседним вершинам. Поскольку вершина “0” уже пройдена, следующая вершина “2”.

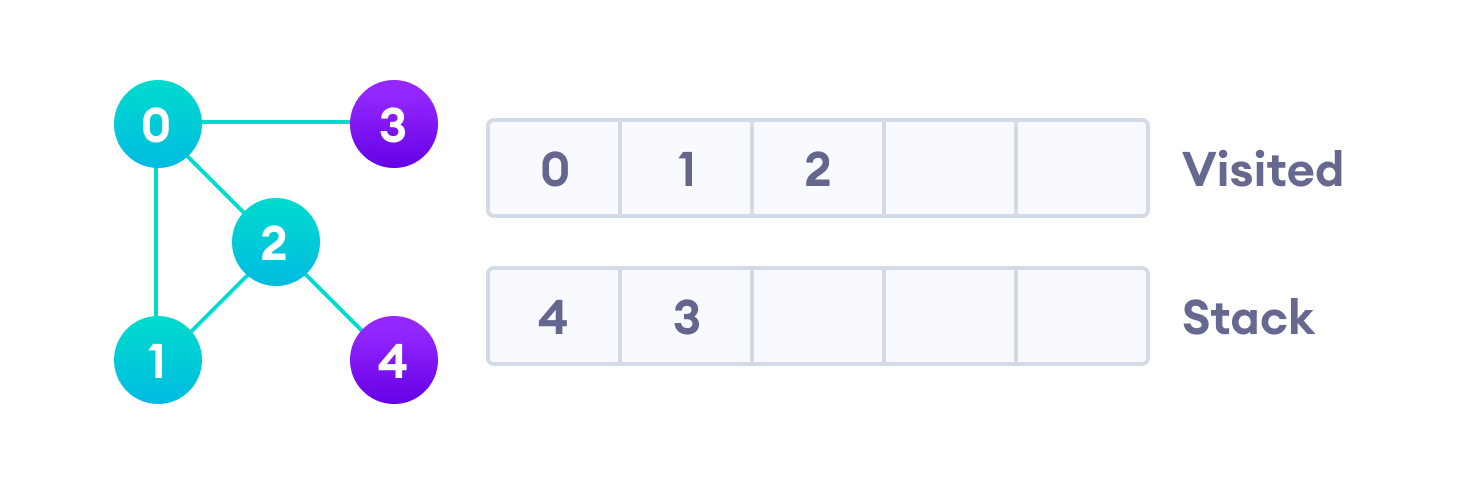
Вершина “2” смежна непройденной вершине “4”, следовательно мы добавляем ее наверх стека и проходим ее.

После того, как мы пройдем последний элемент (вершину “3”), в стеке не останется непройденных смежных вершин, и таким образом мы завершили обход графа в глубину.

Псевдокод поиска в глубину (рекурсивная реализация)

Ниже представлен псевдокод для алгоритма поиска в глубину. Обратите внимание, что в функции init() необходимо запускать функцию DFS на каждой вершине. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому для того, чтобы убедиться, что мы покрываем каждую вершину, мы должны запускать алгоритм поиска в глубину на каждой вершине.

DFS(G, u) u.visited = true for each v ∈ G.Adj[u] if v.visited == false DFS(G,v) init()

Реализация поиска в глубину на Python, Java и C/C++

Ниже приведены примеры реально кода алгоритма поиска в глубину. Код был упрощен, чтобы мы могли сфокусироваться на самом алгоритме, а не на других деталях.

# Алгоритм поиска в глубину на Python # Алгоритм def dfs(graph, start, visited=None): if visited is None: visited = set() visited.add(start) print(start) for next in graph[start] - visited: dfs(graph, next, visited) return visited graph = dfs(graph, '0')

// Алгоритм поиска в глубину на Java import java.util.*; class Graph < private LinkedListadjLists[]; private boolean visited[]; // Создание графа Graph(int vertices) < adjLists = new LinkedList[vertices]; visited = new boolean[vertices]; for (int i = 0; i < vertices; i++) adjLists[i] = new LinkedList(); > // Добавление ребер void addEdge(int src, int dest) < adjLists[src].add(dest); >// Алгоритм void DFS(int vertex) < visited[vertex] = true; System.out.print(vertex + " "); Iteratorite = adjLists[vertex].listIterator(); while (ite.hasNext()) < int adj = ite.next(); if (!visited[adj]) DFS(adj); >> public static void main(String args[]) < Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); System.out.println("Following is Depth First Traversal"); g.DFS(2); >> 

// Алгоритм поиска в глубину на C #include #include struct node < int vertex; struct node* next; >; struct node* createNode(int v); struct Graph < int numVertices; int* visited; // Нам нужен int** для хранения двумерного массива. // Аналогично, нам нужна структура node** для хранения массива связанных списков. struct node** adjLists; >; // Алгоритм void DFS(struct Graph* graph, int vertex) < struct node* adjList = graph->adjLists[vertex]; struct node* temp = adjList; graph->visited[vertex] = 1; printf("Visited %d \n", vertex); while (temp != NULL) < int connectedVertex = temp->vertex; if (graph->visited[connectedVertex] == 0) < DFS(graph, connectedVertex); >temp = temp->next; > > // Создание вершины struct node* createNode(int v) < struct node* newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; > // Создание графа struct Graph* createGraph(int vertices) < struct Graph* graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) < graph->adjLists[i] = NULL; graph->visited[i] = 0; > return graph; > // Добавление ребра void addEdge(struct Graph* graph, int src, int dest) < // Проводим ребро от начальной вершины ребра графа к конечной вершине ребра графа struct node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Проводим ребро из конечной вершины ребра графа в начальную вершину ребра графа newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; > // Выводим граф void printGraph(struct Graph* graph) < int v; for (v = 0; v < graph->numVertices; v++) < struct node* temp = graph->adjLists[v]; printf("\n Adjacency list of vertex %d\n ", v); while (temp) < printf("%d ->", temp->vertex); temp = temp->next; > printf("\n"); > > int main()

// Алгоритм прохода в глубину в C++ #include #include using namespace std; class Graph < int numVertices; list*adjLists; bool *visited; public: Graph(int V); void addEdge(int src, int dest); void DFS(int vertex); >; // Инициализация графа Graph::Graph(int vertices) < numVertices = vertices; adjLists = new list[vertices]; visited = new bool[vertices]; > // Добавление ребер void Graph::addEdge(int src, int dest) < adjLists[src].push_front(dest); >// Алгоритм void Graph::DFS(int vertex) < visited[vertex] = true; listadjList = adjLists[vertex]; cout << vertex << " "; list::iterator i; for (i = adjList.begin(); i != adjList.end(); ++i) if (!visited[*i]) DFS(*i); > int main()

Сложность алгоритма поиска в глубину

Временная сложность алгоритма поиска в глубину представлена ​​в виде O(V + E), где V — количество вершин, а E — количество ребер.

Пространственная сложность алгоритма равна O(V).

Применения алгоритма

1. Для поиска пути.
2. Для проверки двудольности графа.
3. Для поиска сильно связанных компонентов графа.
4. Для обнаружения циклов в графе.

Приглашаем всех желающих на открытый урок в OTUS «Теория графов. Термины и определения. Основные алгоритмы», регистрация доступна по ссылке.

Источник