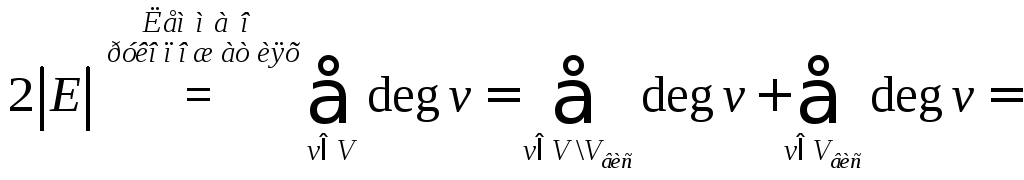- Введение в деревья
- Дерево и его свойства
- Центры и Би-Центры Дерева
- Алгоритм нахождения центров и бицентров дерева
- Маркированные деревья
- пример
- Немеченые деревья
- пример
- Укорененное дерево
- Двоичное дерево поиска
- Лекция 11
- Базовые понятия и утверждения
- 1. Определение и основные свойства деревьев.
- 3.9. Деревья и леса
Введение в деревья
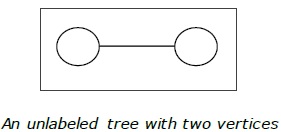
Дерево – это дискретная структура, которая представляет иерархические отношения между отдельными элементами или узлами. Дерево, в котором родитель имеет не более двух детей, называется бинарным деревом.
Дерево и его свойства
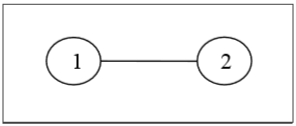
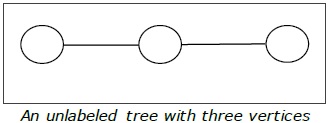
Определение – Дерево – это связный ациклический неориентированный граф. Между каждой парой вершин в G существует уникальный путь. Дерево с N числом вершин содержит ( N − 1 ) число ребер. Вершина, которая имеет 0 градусов, называется корнем дерева. Вершина, имеющая 1 градус, называется листовым узлом дерева, а степень внутреннего узла составляет не менее 2.
Пример . Ниже приведен пример дерева.
Центры и Би-Центры Дерева
Центр дерева – это вершина с минимальным эксцентриситетом. Эксцентриситет вершины X в дереве G – это максимальное расстояние между вершиной X и любой другой вершиной дерева. Максимальный эксцентриситет – диаметр дерева. Если у дерева есть только один центр, оно называется Центральным деревом, а если у дерева есть только несколько центров, оно называется Би-центральным деревом. Каждое дерево является либо центральным, либо двухцентральным.
Алгоритм нахождения центров и бицентров дерева
Шаг 1 – Удалите все вершины степени 1 из данного дерева, а также удалите их падающие ребра.
Шаг 2 – Повторяйте шаг 1, пока не останется одна вершина или две вершины, соединенные ребром. Если осталась одна вершина, то это центр дерева, а если осталось две вершины, соединенные ребром, то это бицентр дерева.
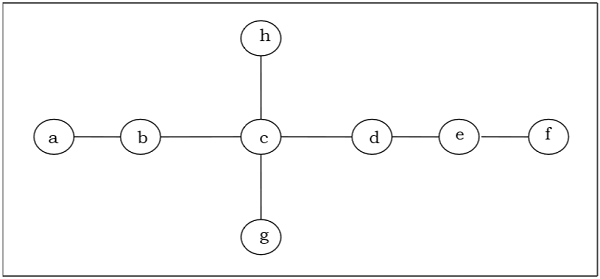
Узнайте центр / би-центр следующего дерева –
Сначала мы удалим все вершины степени 1, а также удалим их падающие ребра и получим следующее дерево:
Опять же, мы удалим все вершины степени 1, а также удалим их инцидентные ребра и получим следующее дерево:
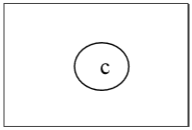
Наконец, мы получили одну вершину «c» и остановили алгоритм. Поскольку существует единственная вершина, у этого дерева есть один центр ‘c’, и дерево является центральным деревом.
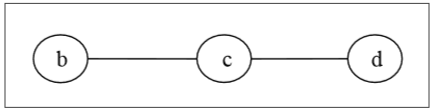
Узнайте центр / би-центр следующего дерева –
Сначала мы удалим все вершины степени 1, а также удалим их падающие ребра и получим следующее дерево:
Опять же, мы удалим все вершины степени 1, а также удалим их инцидентные ребра и получим следующее дерево:
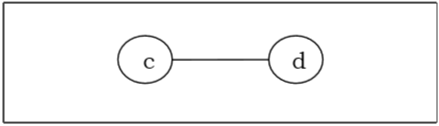
Наконец, у нас осталось две вершины «c» и «d», поэтому мы останавливаем алгоритм. Поскольку оставлены две вершины, соединенные ребром, это дерево имеет двухцентровый «cd», а дерево является двухцентровым.
Маркированные деревья
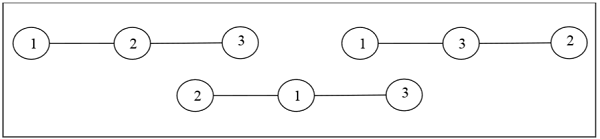
Определение – помеченное дерево – это дерево, вершинам которого присваиваются уникальные номера от 1 до n. Мы можем посчитать такие деревья для малых значений n вручную, чтобы предположить общую формулу. Число помеченных деревьев из n вершин равно n n − 2 . Два помеченных дерева изоморфны, если их графы изоморфны и соответствующие точки двух деревьев имеют одинаковые метки.
пример
Немеченые деревья
Определение – немеченое дерево – это дерево, вершинам которого не назначены никакие числа. Число помеченных деревьев с числом вершин n равно $ \ frac <(N + 1)! N! >$ (n- е каталонское число)
пример
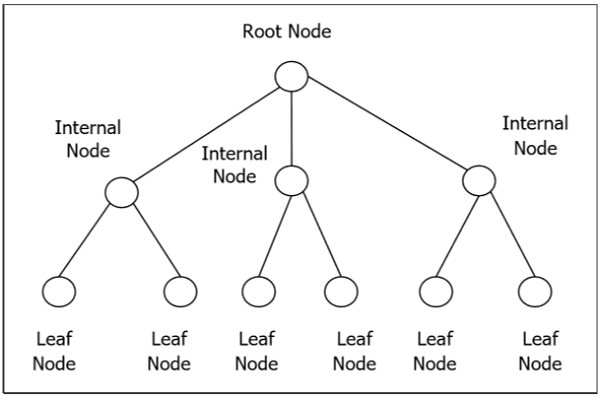
Укорененное дерево
Корневое дерево G – это связный ациклический граф со специальным узлом, который называется корнем дерева, и каждое ребро прямо или косвенно происходит от корня. Упорядоченное корневое дерево – это корневое дерево, в котором упорядочены дочерние элементы каждой внутренней вершины. Если каждая внутренняя вершина корневого дерева имеет не более m дочерних элементов, она называется m-арным деревом. Если каждая внутренняя вершина корневого дерева имеет ровно m детей, она называется полным m-арным деревом. Если m = 2 , корневое дерево называется бинарным деревом.
Двоичное дерево поиска
Двоичное дерево поиска – это двоичное дерево, которое удовлетворяет следующему свойству:
- X в левом поддереве вершины V , V a l u e ( X ) l e V a l u e ( V )
- Y в правом поддереве вершины V , V a l u e ( Y ) g e V a l u e ( V )
Таким образом, значение всех вершин левого поддерева внутреннего узла V меньше или равно V , а значение всех вершин правого поддерева внутреннего узла V больше или равно V . Количество ссылок от корневого узла к самому глубокому узлу является высотой дерева двоичного поиска.
Источник
Лекция 11
Дерево. Лес (ациклический граф). Остовный подграф. Остов. Взвешенный граф. Минимальный остов. Кодирование деревьев.
Базовые понятия и утверждения
1. Определение и основные свойства деревьев.
Определение. Граф называется деревом, если он связный и в нем нет циклов.
Одноэлементный граф, т.е. граф, имеющий одну вершину и не имеющий ребер, также считается деревом.
Граф называется лесом (или ациклическим графом), если в нем нет циклов. Очевидно, что каждая компонента связности леса — дерево.
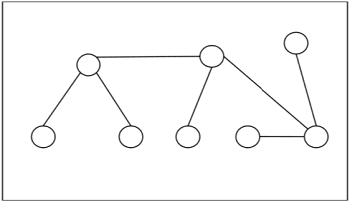
Пример 1. Граф 


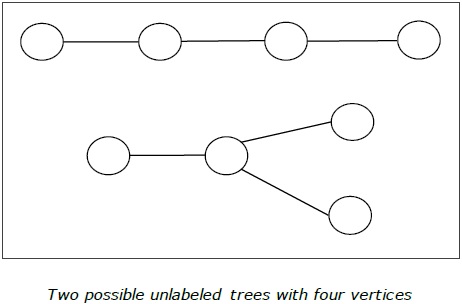
Пример 2. Представьте диаграммами все (с точностью до изоморфизма) деревья с пятью вершинами.
◄ Имеется три различных (с точностью изоморфизма) дерева с пятью вершинами (рис. 3.22 — 3.24). ►
Деревья обладают рядом характеристических свойств, по наличию или отсутствию каждого их которых в рассматриваемом графе можно определить, является граф деревом или нет. Перечислим эти свойства:
1) граф 

2) граф 

3) граф — дерево в том и только в том случае, когда он связный, и каждое его ребро является мостом;
4) граф 

5) граф — дерево в том и только в том случае, когда в нем нет циклов и добавление к нему нового ребра приводит к образованию единственного простого цикла.
Также приведем одно из характеристических свойств леса: граф 


2. Остовы графа. Подграф 


Остовом обыкновенного графа называется его остовный подграф, являющийся деревом.
Пусть 







Пусть теперь 






.
Таким образом, чтобы получить остовный подграф, нужно, последовательно разрушая циклы графа, удалить из него число ребер, равное его цикломатическому числу.
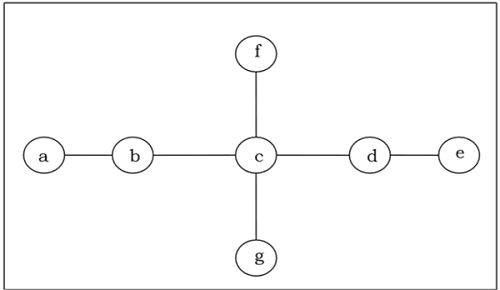
Пример 3. Построим остов графа 










Источник
3.9. Деревья и леса
Каждая компонента связности леса – дерево, следовательно, для 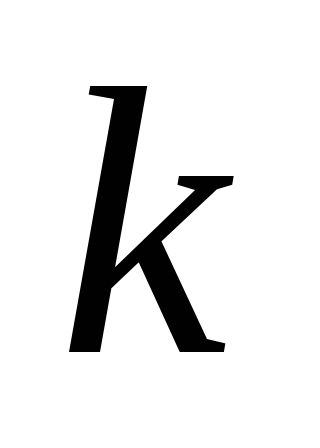

П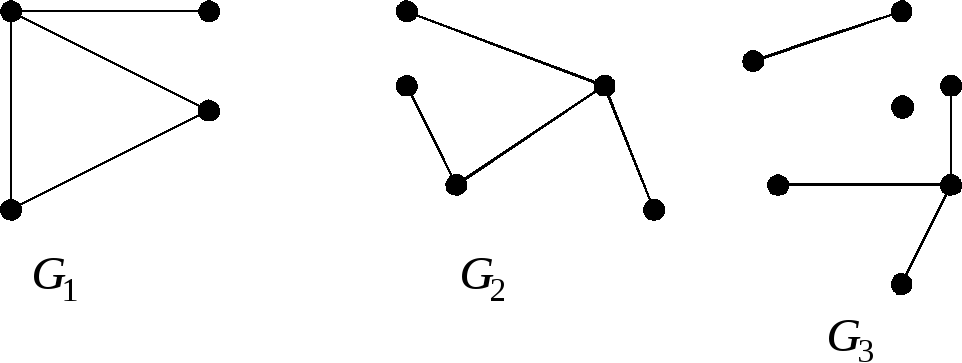

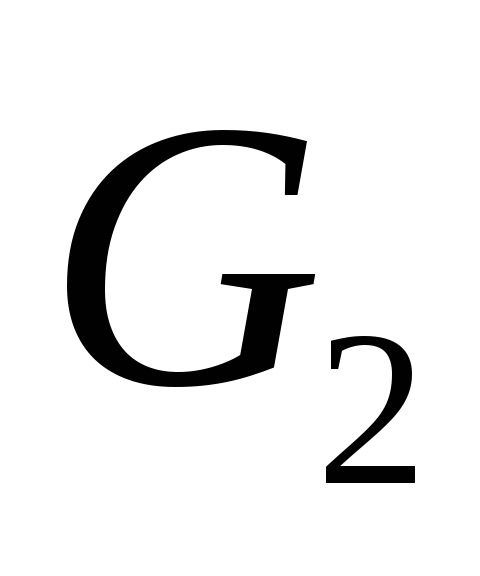

Лемма. Если граф – дерево, то каждое его ребро является мостом.
Доказательство.В параграфе 3.6 было доказано, что если ребро графа не содержится ни в одном цикле, то оно является мостом. Дерево граф ациклический, следовательно, каждое его ребро мост.■
Теорема (основная теорема о деревьях). Для графа следующие утверждения равносильны:
- Граф
— дерево.
ациклический и
.
связный и
.
связный и каждое его ребро является мостом.
- Любые две вершины графа
можно соединить, притом единственной, простой цепью.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
Доказательство.Доказательство проведем по следующей схеме:


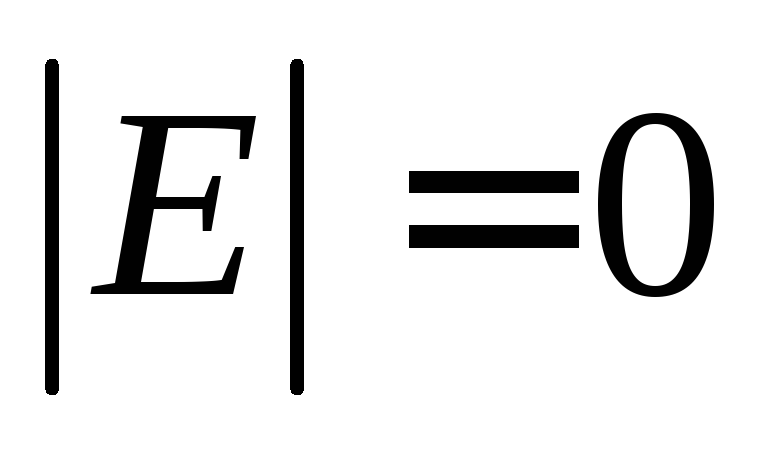
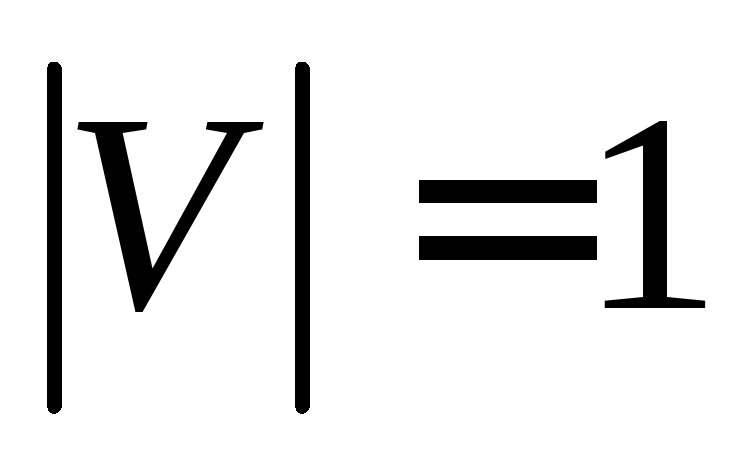
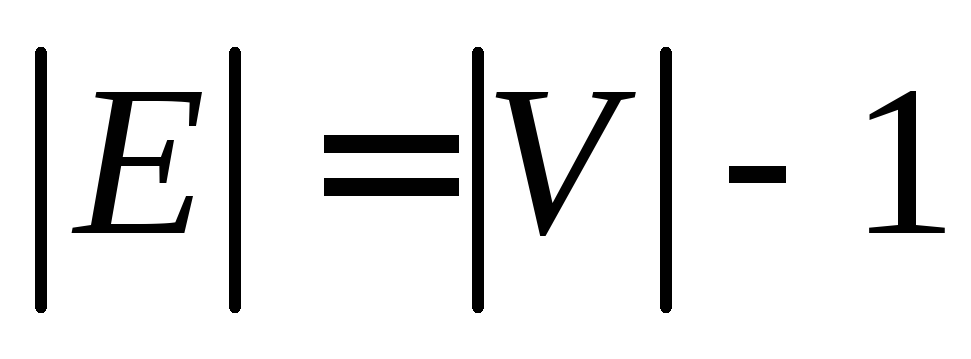




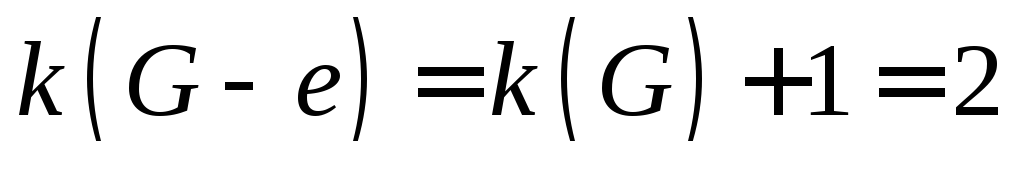
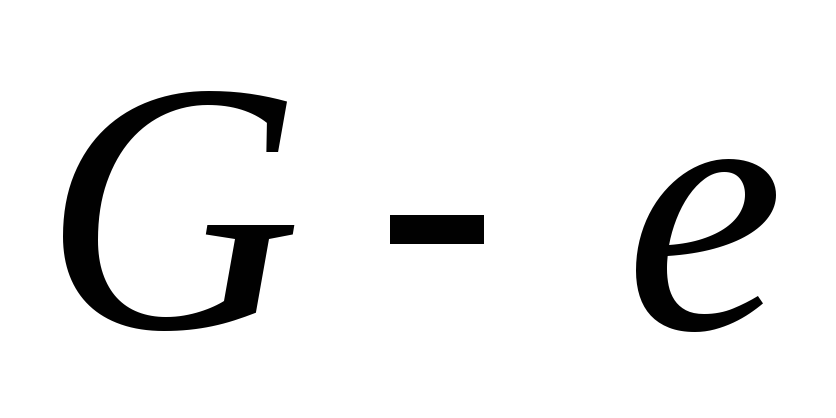
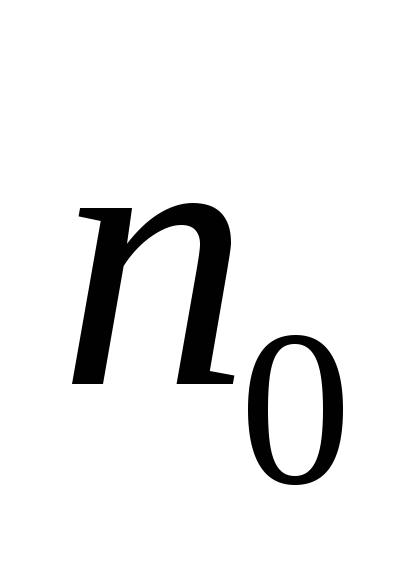
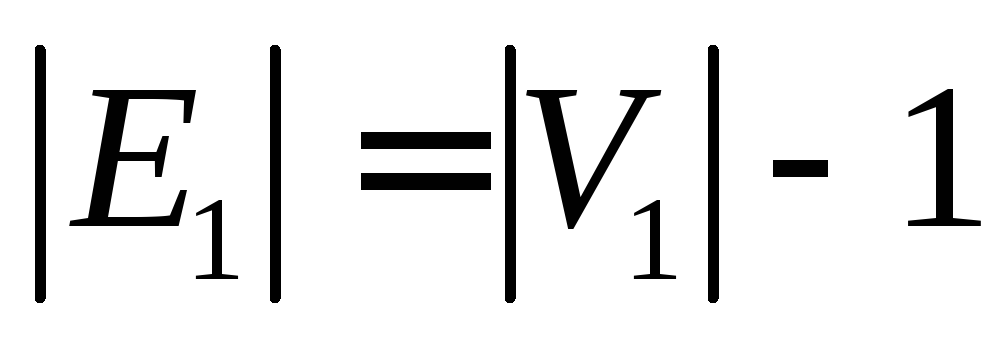
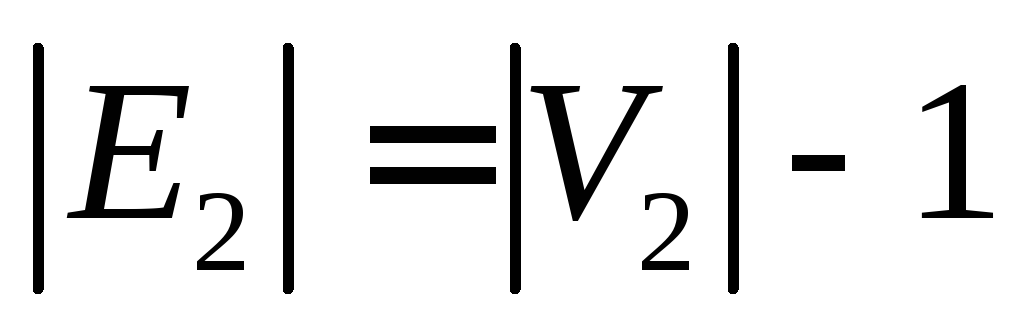



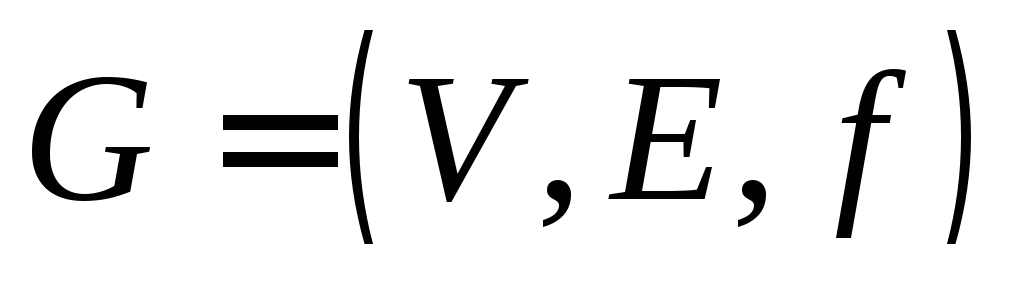
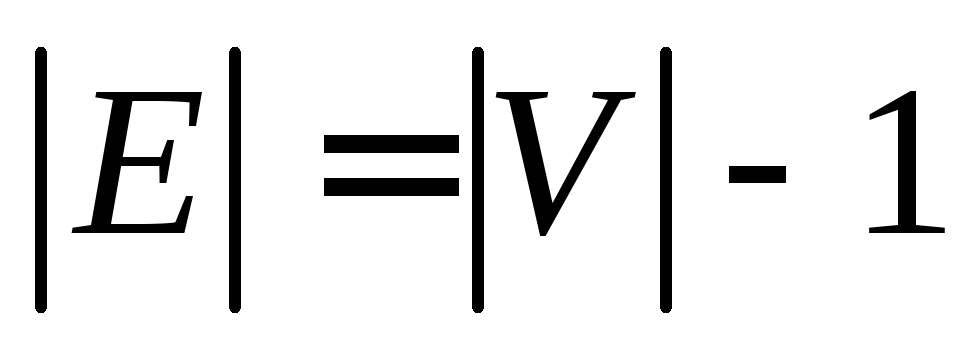

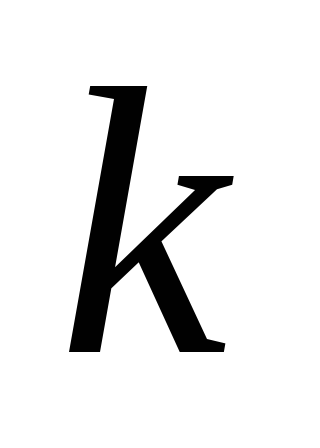











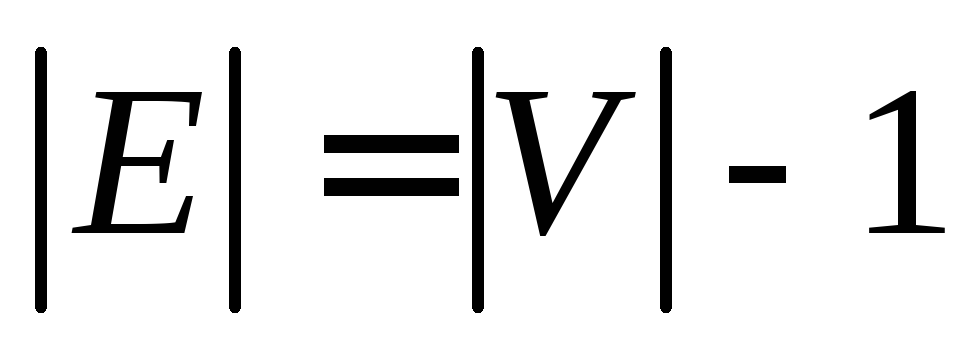



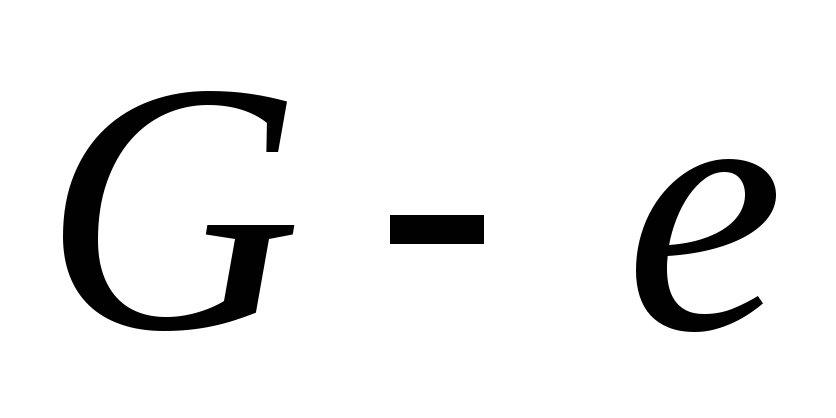
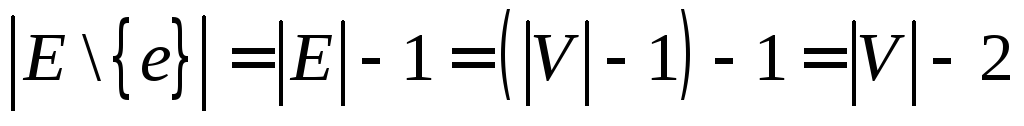
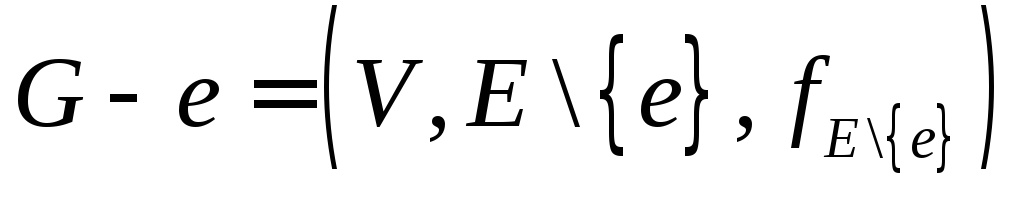











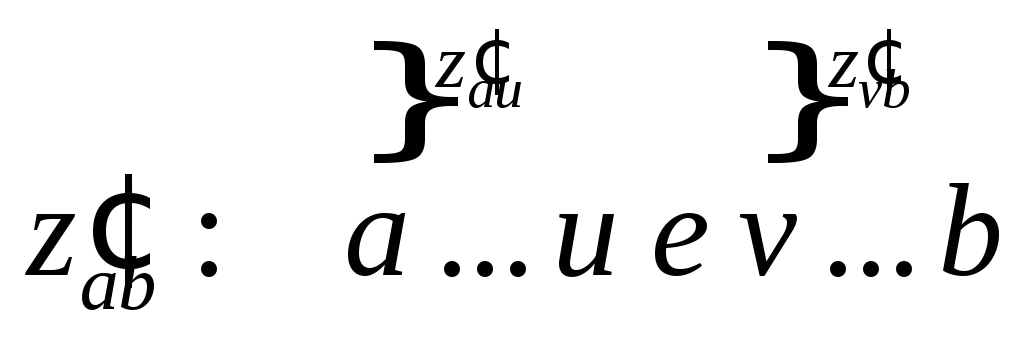



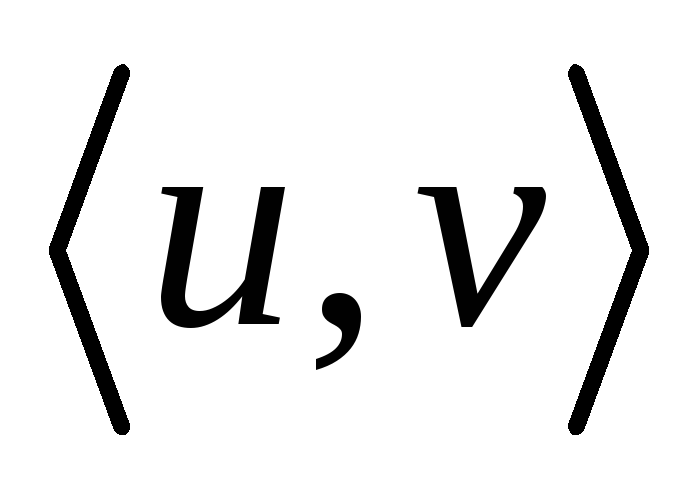

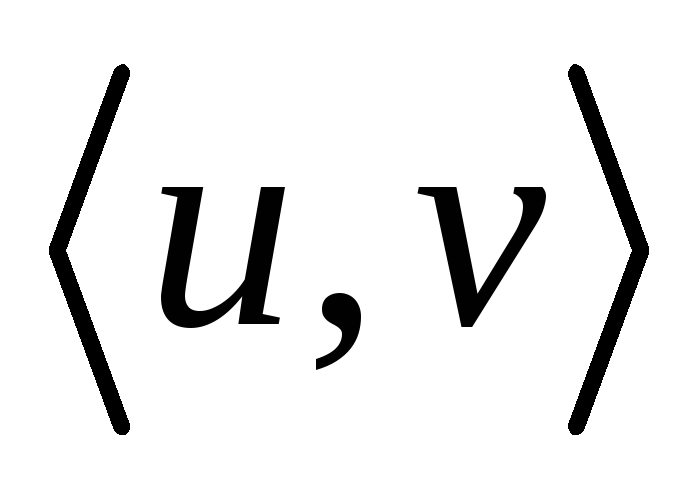
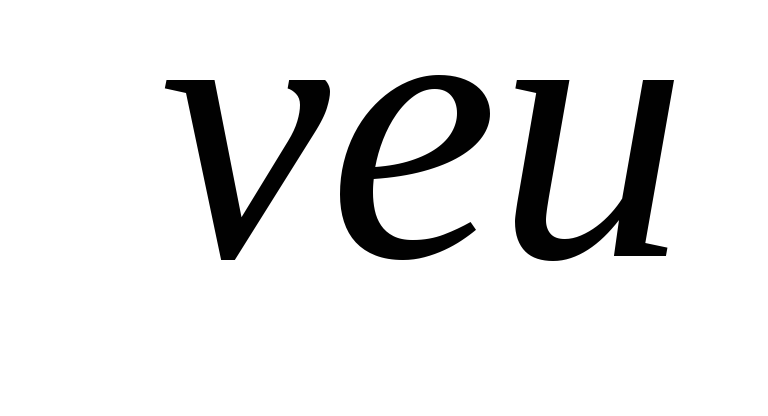

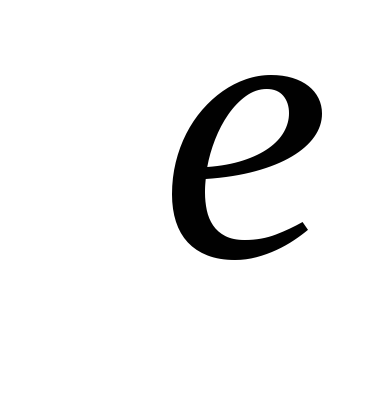






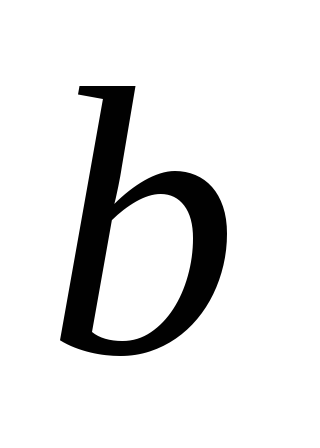







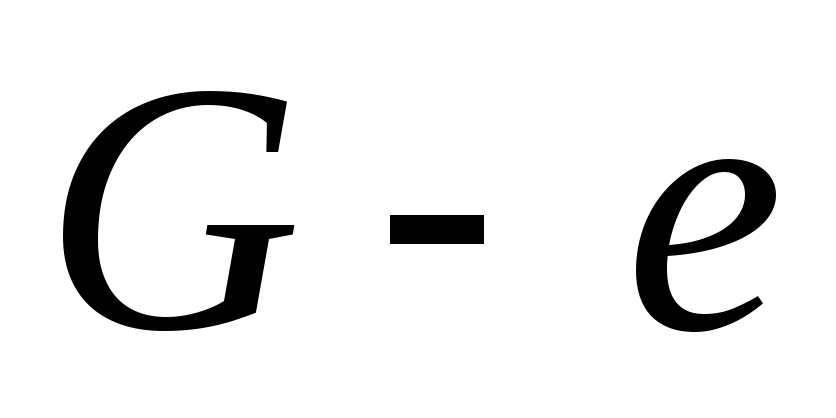

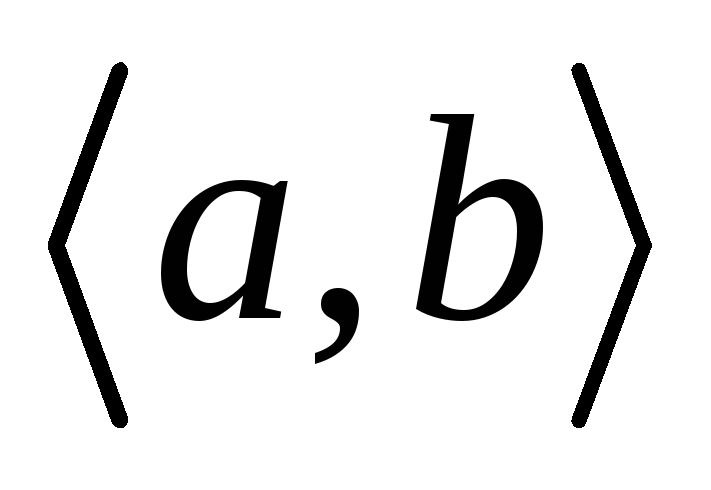








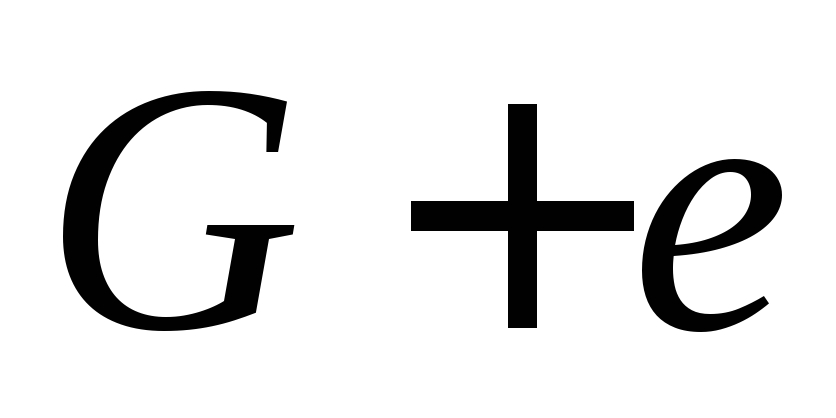

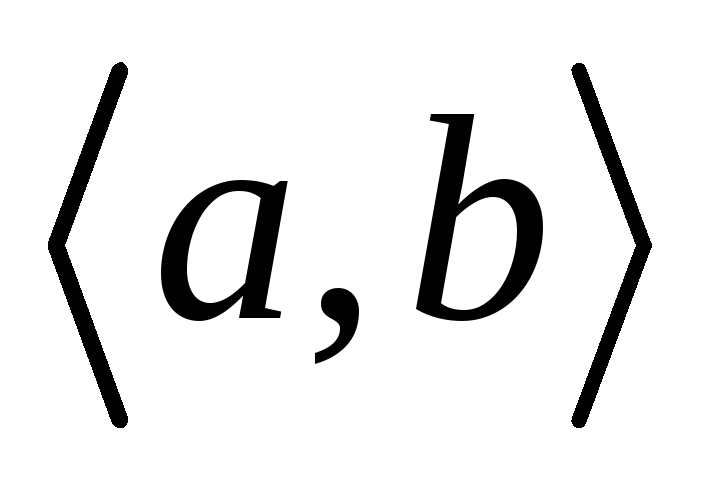

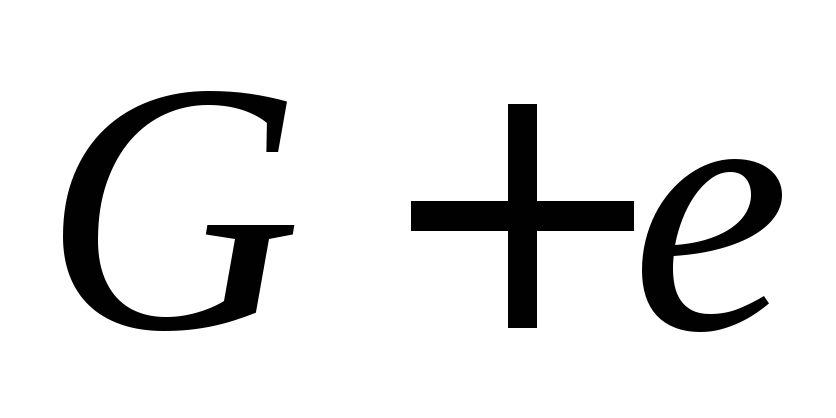
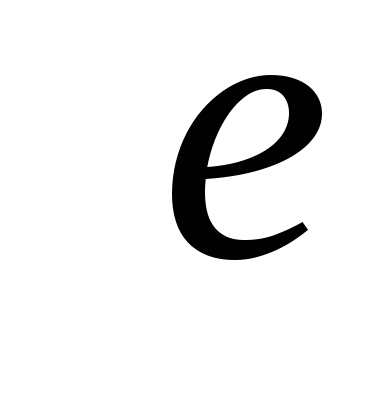
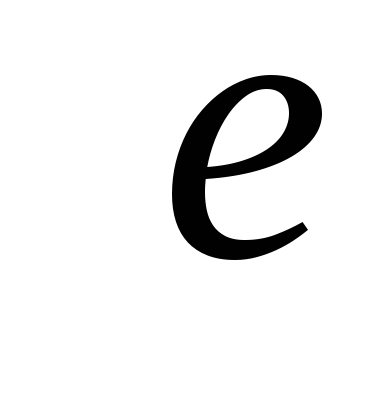

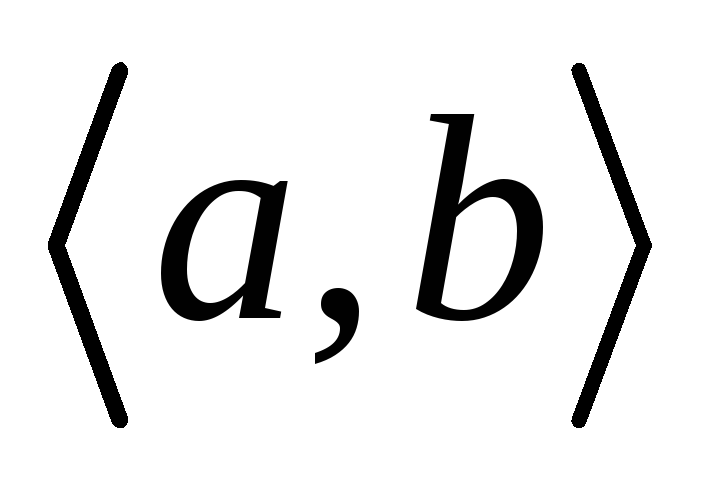




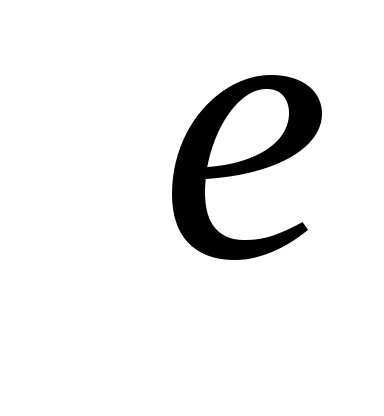
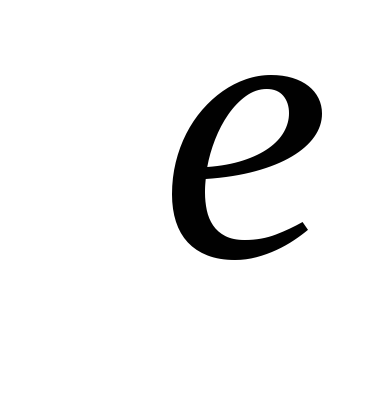



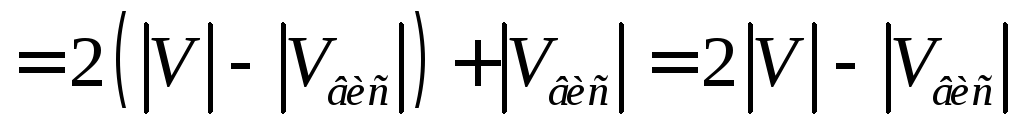




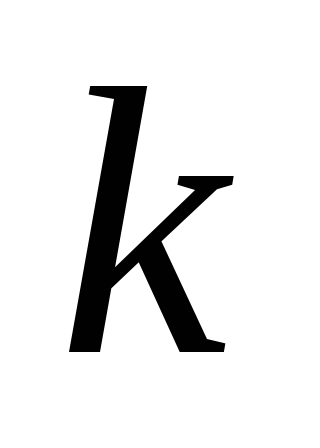

Источник














 — дерево.
— дерево. ациклический и
ациклический и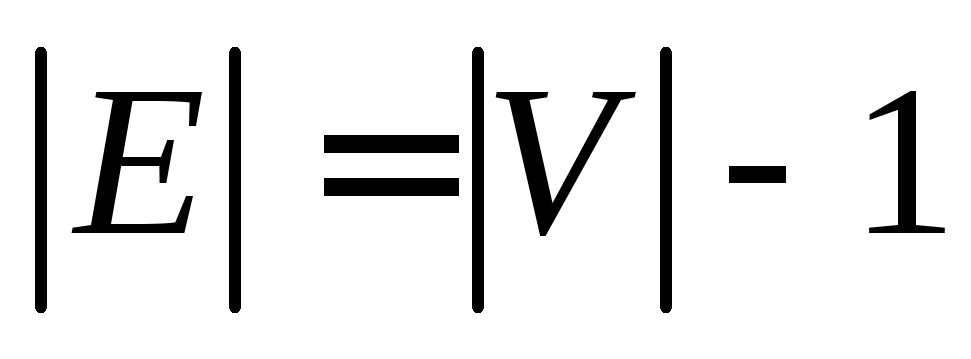 .
. связный и
связный и .
. связный и каждое его ребро является мостом.
связный и каждое его ребро является мостом. можно соединить, притом единственной, простой цепью.
можно соединить, притом единственной, простой цепью. ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.