Дерево отрезков. Построение
Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера [math]N*N[/math] , объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов.
При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[l \ldots r][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.
Структура
Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по [math]2[/math] ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0\ldots n-1][/math] , левый ребёнок корня содержит результат функции на [math][0\ldots\dfrac][/math] , а правый, соответственно результат на [math][\dfrac+1\ldots n-1][/math] . И так далее, продвигаясь вглубь дерева.
Построение дерева
Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math] , где [math]2^k \geqslant n[/math] . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой [math]n+\dfrac+\dfrac \ldots +1 \lt 2n[/math] , где [math]n=2^k[/math] . Таким образом, структура занимает линейную память.
Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.
Реализация построения сверху:
function treeBuild(T a[], int i, int tl, int tr): // мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr) if tr - tl == 1 t[i] = a[tl] else tm = (tl + tr) / 2 // середина отрезка treeBuild(a, 2 * i + 1, tl, tm) treeBuild(a, 2 * i + 2, tm, tr) t[i] = t[2 * i + 1] t[2 * i + 2] Реализация построения снизу:
function treeBuild(T a[]): for i = 0 to n - 1 t[n - 1 + i] = a[i] for i = n - 2 downto 0 t[i] = t[2 * i + 1] t[2 * i + 2] См. также
Источники информации
Источник
Задача RMQ – 2. Дерево отрезков
В первой части нашей темы мы рассмотрели решение задачи static RMQ за (O(nlogn), O(1)). Теперь мы разберёмся со структурой данных, называемой дерево отрезков, или интервалов (в англоязычной литературе – segment tree или interval tree). С помощью неё можно решать dynamic RMQ за (O(n), O(logn)).
Определение
Введём понятие дерева отрезков. Для удобства дополним длину массива до степени двойки. В добавленные элементы массива допишем бесконечности (за бесконечностью стоит понимать, например, число, больше которого в данных ничего не появится). Итак, дерево отрезков это двоичное дерево, в каждой вершине которого написано значение заданной функции на некотором отрезке. Функция в нашем случае – это минимум.
Каждому листу будет соответствовать элемент массива с номером, равным порядковому номеру листа в дереве. А каждой вершине, не являющейся листом, будет соответствовать отрезок из элементов массива соответствующих листам-потомкам этой вершины.
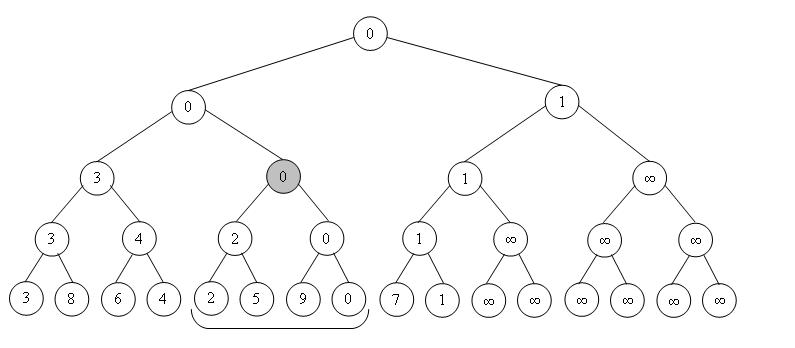
За кажущейся монструозностью определения скрывается вполне простое понятие – обращаем взгляд на рисунок.
Поясним определение. Выделенной вершине будет соответствовать отмеченный отрезок, потому как он является объединением всех листов-потомков данной вершины (начиная с этого момента отождествим лист и элемент массива, который он представляет).
Хранить дерево будем подобно двоичной куче. Заведём массив T[2n – 1]. Корень будет лежать в первом элементе массива, а сыновья i-ой вершины будут лежать в элементах с номерами 2i и 2i + 1 – левый и правый соответственно. Сразу можно заметить очевидное свойство: T[i] = min(T[2i], T[2i + 1]) для i-ой вершины, не являющейся листом. Листы, к слову, будут лежать при такой нумерации в элементах с номерами от n до 2n – 1.
Построение
Построим дерево, пробежавшись по элементам с (n – 1)-ого по первый, считая минимум значений в сыновьях для каждой вершины.
Начиная с этой статьи я буду давать код для большей наглядности.
const int INF = INT_MAX; void build_tree(const vector& V) < // размер, доведённый до степени двойки int n = (1 0; i--) V[i] = min(V[2 * i], V[2 * i + 1]); > Функция build_tree(V) превращает массив V в дерево отрезков для этого массива. Итак, как теперь по отрезку найти минимум на нём? Для этого введём понятие фундаментального отрезка.
Запрос минимума
Назовём фундаментальным отрезком в массиве такой отрезок, что существует вершина в дереве, которой он соответствует. Разобьём наш отрезк на минимальное количество непересекающихся фундаментальных. Покажем, что на каждом уровне их количество не превосходит 2.
Возьмём самый большой фундаментальный отрезок в разбиении. Пусть его длина – 2t. Заметим, что фундаментальных отрезков длиной 2t – не более двух (1). Возьмём самый левый из имеющихся максимальных фундаментальных. Будем двигаться от него налево. Заметим, опять же, что длины отрезков будут убывать (2). Так же и с правым из максимальных. Тем самым получим, что фундаментальных отрезков – не более 2t, что не превосходит 2logn. Пункты (1) и (2) в доказательстве я оставлю для самостоятельного осмысления.
Чем нам это помогает? Теперь мы можем реализовать запрос минимума «снизу». Будем подниматься снизу, добавляя к ответу на каждом уровне, если надо, фундаментальный отрезок.
Заведём два указателя – l и r, с помощью которых будем находить очередные фундаментальные отрезки разбиения. Изначально установим l и r указывающими на листы, соответствующие концам отрезка запроса. Заметим, что если l указывает на вершину, являющуюся правым сыном своего родителя, то эта вершина принадлежит разбиению на фундаментальные отрезки, в противном случае не принадлежит. Аналогично с указателем r – если он указывает на вершину, являющуюся левым сыном своего родителя, то добавляем её в разбиение. После этого сдвигаем оба указателя на уровень выше и повторяем операцию. Продолжаем операции пока указатели не зайдут один за другой.
Находя очередной фундаментальный отрезок, мы сравниваем минимум на нём с текущим найденным минимумом и уменьшаем его в случае необходимости. Асимптотика работы алгоритма – O(logn), т. к. на каждом уровне мы выполняем константное число операций, а всего уровней – logn.
Модификация
Теперь научимся изменять значение элемента дерева. Заметим, что для каждого листа есть ровно logn фундаментальных отрезков, которые его содержат – все они соответствуют вершинам, лежащим на пути от нашего листа до корня.
Значит, при изменении элемента достаточно просто пробежаться от его листа до корня и обновить значение во всех вершинах на пути по формуле T[i] = min(T[2i], T[2i + 1]).
void update(vector& T, int i, int x) < int n = T.size() / 2; i += n – 1; T[i] = x; while (i /= 2) T[i] = min(T[2 * i], T[2 * i + 1]); >Ура! Получаем решение задачи Dynamic RMQ за (O(n), O(logn)).
В следующей статье мы научимся делать запрос сверху. Несмотря на то, что асимптотика у запроса сверху будет такая же, у него есть одна большая плюшка – возможность легко и непринуждённо прикрутить модификацию на отрезке. До новых встреч!
Источник
Дерево отрезков
Дерево отрезков — структура данных, позволяющая выполнять многие операции с отрезками массива за \(O(\log N)\). Дерево отрезков — универсальная структура данных, для которой можно реализовать неограниченный набор операций (иногда за большую сложность: \(O(\log^2 N)\)). Самая простая версия дерева отрезков позволяет находить сумму или минимум на отрезке, и изменять отдельные элементы.
Построение дерева отрезков
Дерево отрезков — полное бинарное дерево, в котором каждая вершина отвечает за некоторый отрезок в массиве. Корень дерева отвечает за весь массив, его две дочерних вершины — за две половины, и так далее. У каждой вершины, отвечающей за отрезок длиной больше \(1\), есть две дочерних вершины, отвечающих за левую и правую половины этого отрезка. Листья дерева отрезков отвечают за отдельные элементы (отрезки длиной \(1\)).
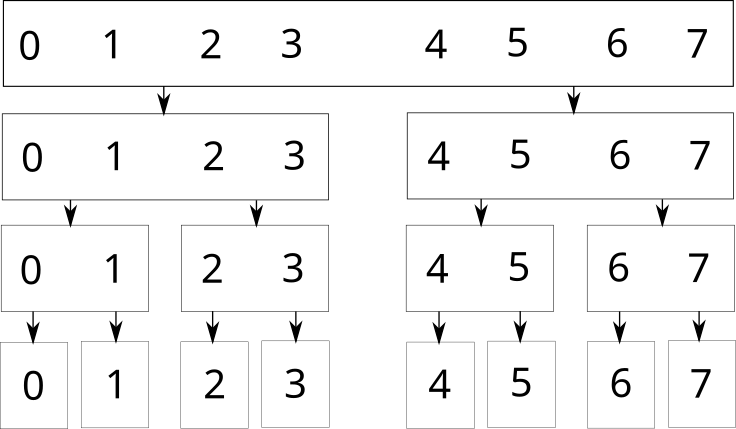
Графически это выглядит следующим образом (для массива из 8 элементов):
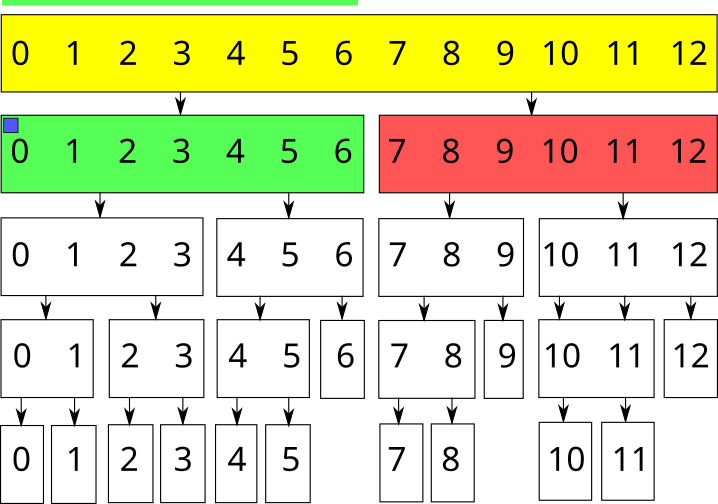
Каждый прямоугольник — вершина дерева отрезков. Если некоторая вершина отвечает за отрезок нечётной длины, то одна из её дочерних вершин будет отвечать за отрезок длиной \(\lceil \rceil\), а другая — за отрезок длиной \(\lfloor \rfloor\). Например, так выглядит дерево отрезков для массива из 13 элементов:
Для массива из \(n\) элементов дерево отрезков имеет около \(2n\) вершин (\(n + + + \ldots\)), а его высота равна порядка \(\log n\).
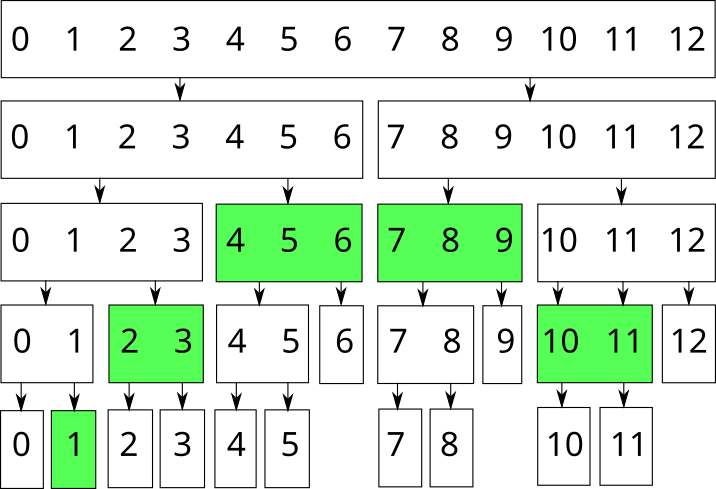
Главное свойство дерева отрезков, на котором и строятся все алгоритмы работы с ним: любой непрерывный отрезок в массиве из \(n\) элементов можно представить с помощью около \(2 \log n\) вершин в дереве отрезков.
Например, отрезок \([1; 11]\) в массиве длиной \(13\) можно представить с помощью следующих вершин:
Дерево отрезков для поиска суммы
Одна из простейших функций, которую можно считать за \(O(\log N)\) с помощью дерева отрезков — сумма.
При построении дерева в каждой его вершине сохраним сумму на соответствующем отрезке (построение будет вестись рекурсивно, поэтому достаточно просто сложить суммы на двух дочерних отрезках). Затем каждый запрос суммы на отрезке будем разбивать на \(2 \log N\) отрезков, и находить сумму на каждом из них за \(O(1)\), используя предпросчитанные значения. Таким образом сложность запроса суммы равна \(O(\log N)\).
Кроме запросов суммы к дереву отрезков также могут поступать запросы на изменение отдельных элементов (модификацию). Заметим, что от изменения одного элемента значение суммы изменится в одной вершине на каждом уровне дерева отрезков (в которую входит этот элемент). Пересчитаем значения суммы (опять же, рекурсивно) только в этих вершинах. Таким образом сложность запроса модификации равна высоте дерева, или \(O(\log N)\).
Для реализации запроса суммы и запроса модификации обход дерева реализуется с помощью одного и того же алгоритма, основанного на DFS. Пусть границы нашего запроса \([L; R]\) (в случае запроса модификации \(L = R\)), а границы отрезка, соответствующего текущей вершине \([TL; TR]\). В зависимости от взаимного положения этих границ, существуют три варианта действий алгоритма:
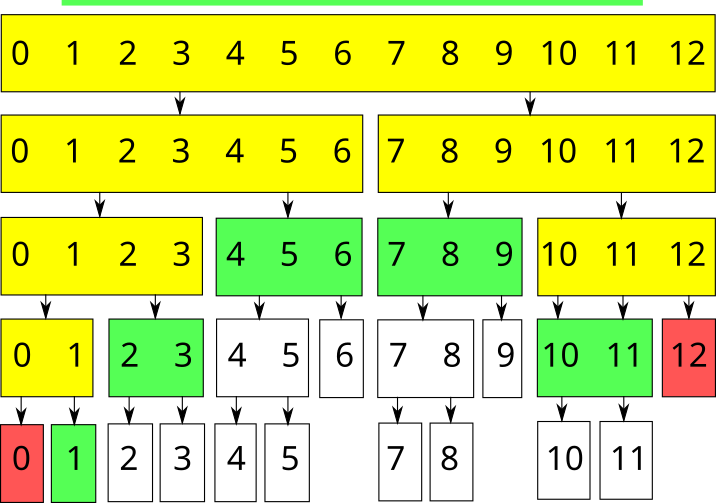
- Текущий отрезок полностью входит в запрос (\(L \le TL; TR \le R\)). Если это запрос суммы, вернём предпросчитанную сумму на отрезке. Если это запрос модификации, изменим элемент и пересчитаем сумму. В дочерние вершины спускаться нет надобности.
- Текущий отрезок полностью не входит в запрос (\(TR < L\) или \(R < TL\)). Никаких действий выполнять не нужно, просто выйдем из функции. Если это запрос суммы, просто вернём \(0\).
- Текущий отрезок частично входит в запрос. Вызовем функцию рекурсивно для двух дочерних отрезков. Если это запрос суммы, вернём сумму двух полученных значений. Если это запрос модификации, пересчитаем значение суммы для текущего отрезка (так как оно могло измениться).
Обозначим эти варианты соответственно зелёным, красным и жёлтым цветом. Тогда запрос суммы на отрезке \([1; 11]\) массива длиной \(13\) будет обработан следующим образом:
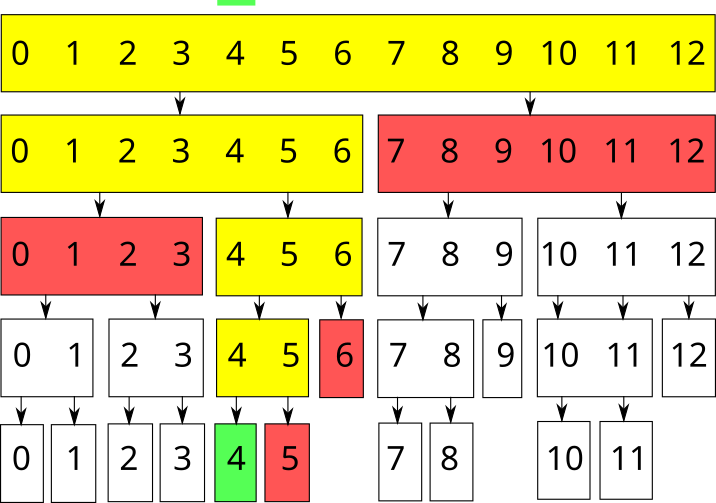
А запрос модификации \(4\)-го элемента:
Реализация дерева отрезков для поиска суммы
Полное бинарное дерево представляем, как и, например, кучу, с помощью массива и формул перехода \(l = 2v\) и \(r = 2v + 1\). Для предотвращения всех возможных переполнений размер дерева отрезков для массива из \(n\) элементов принимают равным \(4n\).
brestprog
Источник