Дерево отрезков построение снизу

Дерево отрезков. Построение

Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера [math]N*N[/math] , объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов.

При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[l \ldots r][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.

Структура

Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по [math]2[/math] ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0\ldots n-1][/math] , левый ребёнок корня содержит результат функции на [math][0\ldots\dfrac][/math] , а правый, соответственно результат на [math][\dfrac+1\ldots n-1][/math] . И так далее, продвигаясь вглубь дерева.

Построение дерева

Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math] , где [math]2^k \geqslant n[/math] . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой [math]n+\dfrac+\dfrac \ldots +1 \lt 2n[/math] , где [math]n=2^k[/math] . Таким образом, структура занимает линейную память.

Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.

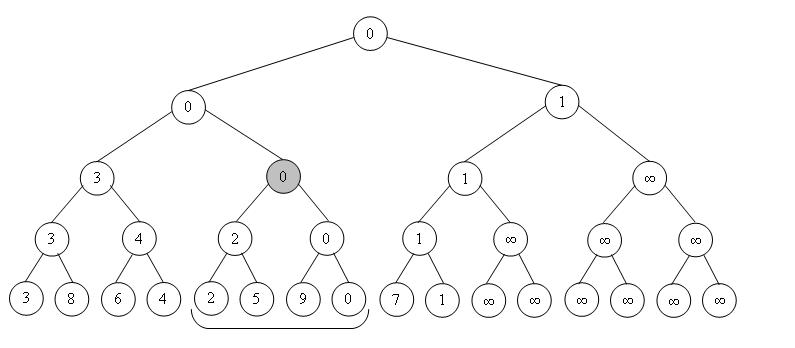
Реализация построения сверху:

function treeBuild(T a[], int i, int tl, int tr): // мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr) if tr - tl == 1 t[i] = a[tl] else tm = (tl + tr) / 2 // середина отрезка treeBuild(a, 2 * i + 1, tl, tm) treeBuild(a, 2 * i + 2, tm, tr) t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

Реализация построения снизу:

function treeBuild(T a[]): for i = 0 to n - 1 t[n - 1 + i] = a[i] for i = n - 2 downto 0 t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

См. также

Источники информации

Источник

Реализация запроса в дереве отрезков снизу

Реализация запроса снизу вверх в дереве отрезков является, в отличие от реализации запроса сверху вниз, итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности, и обозначать ее [math]a \circ b[/math] .

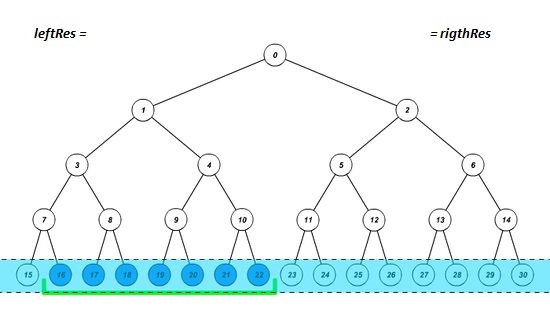
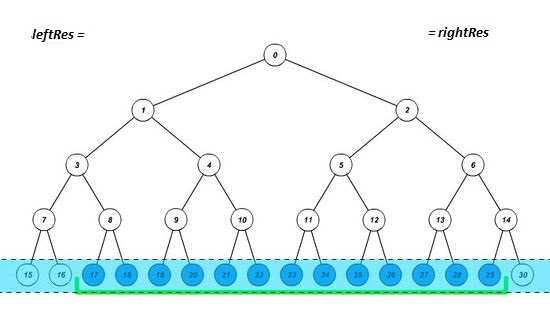
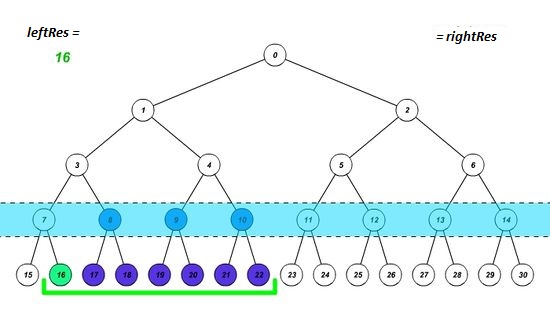
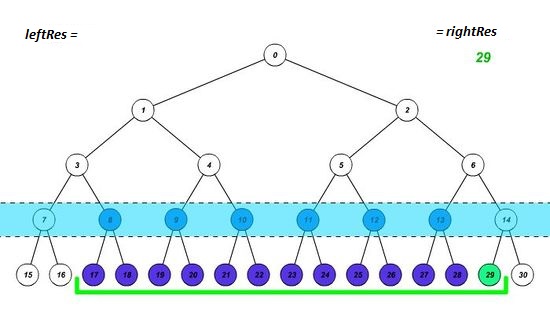
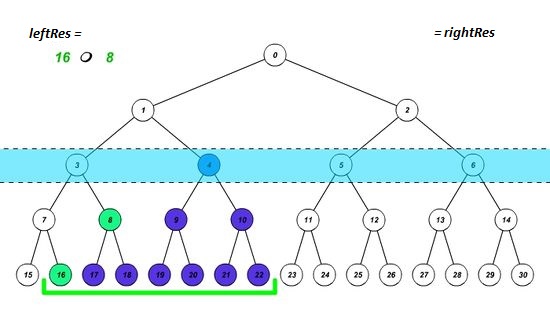
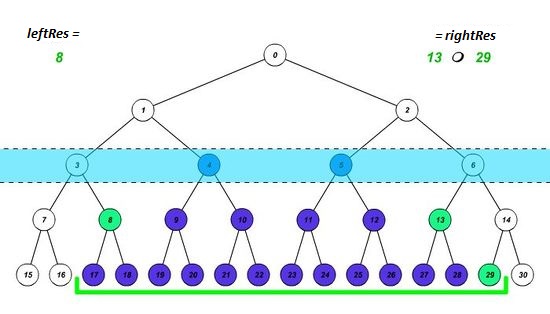
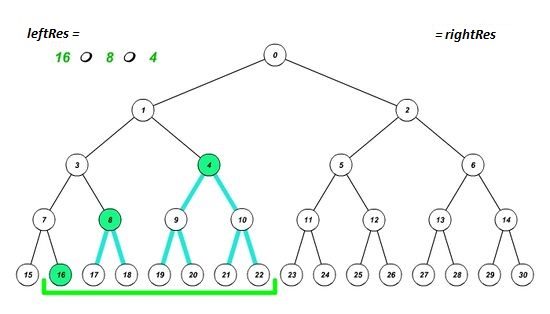
Построим дерево отрезков, и установим границы отрезка на соответствующие им листья. Будем действовать в 3 этапа:

1. Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Аналогично с правой границей (является ли она левым сыном). Таким образом мы учтем вклад нужной нам вершины и избавимся от вклада ненужного нам поддерева.
2. Устанавливаем границы отрезка на родительские элементы текущих границ. Это позволит узнать, входит ли полученный отрезок в искомый или нет. Повторяем этап 1, пока границы не пересекутся.
3. Если после завершения цикла границы совпадут, значит полученный отрезок входит в искомый, и надо пересчитать результат.

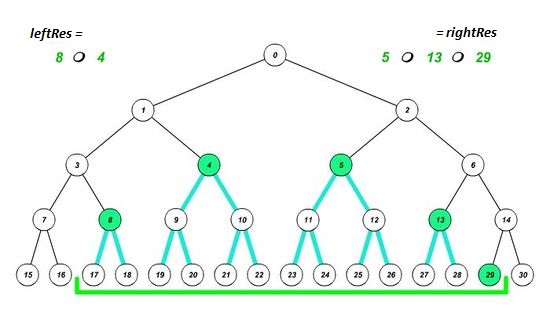
Реализация запроса снизу вверх	Ещё один пример

Псевдокод

Пусть результат считаем на отрезке [math] [left, right] [/math] . При этом значения [math]left[/math] и [math]right[/math] , передающиеся в функцию, должны указывать на листья дерева (необходимо увеличить значение на индекс массива, с которого начинаются листья). Переменные [math]leftRes[/math] и [math]rightRes[/math] будут собирать значения на отрезках, отделившихся соответственно слева или справа от рассматриваемого.

int query(left: int, right: int): leftRes = neutral rightRes = neutral while left < right if left mod 2 == 0 leftRes = leftRes [math] \circ [/math] data[left] left = left div 2 if right mod 2 == 1 rightRes = data[right] [math] \circ [/math] rightRes right = right div 2 - 1 if left == right leftRes = leftRes [math] \circ [/math] data[left] return leftRes [math] \circ [/math] rightRes

См. также

Источники информации

Источник

Дерево отрезков. Построение

Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера [math]N*N[/math] , объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов.

При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[l \ldots r][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.

Структура

Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по [math]2[/math] ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0\ldots n-1][/math] , левый ребёнок корня содержит результат функции на [math][0\ldots\dfrac][/math] , а правый, соответственно результат на [math][\dfrac+1\ldots n-1][/math] . И так далее, продвигаясь вглубь дерева.

Построение дерева

Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math] , где [math]2^k \geqslant n[/math] . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой [math]n+\dfrac+\dfrac \ldots +1 \lt 2n[/math] , где [math]n=2^k[/math] . Таким образом, структура занимает линейную память.

Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.

Реализация построения сверху:

function treeBuild(T a[], int i, int tl, int tr): // мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr) if tr - tl == 1 t[i] = a[tl] else tm = (tl + tr) / 2 // середина отрезка treeBuild(a, 2 * i + 1, tl, tm) treeBuild(a, 2 * i + 2, tm, tr) t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

Реализация построения снизу:

function treeBuild(T a[]): for i = 0 to n - 1 t[n - 1 + i] = a[i] for i = n - 2 downto 0 t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

См. также

Источники информации

Источник

Дерево отрезков. Построение

Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера [math]N*N[/math] , объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов.

При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[l \ldots r][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.

Структура

Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по [math]2[/math] ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0\ldots n-1][/math] , левый ребёнок корня содержит результат функции на [math][0\ldots\dfrac][/math] , а правый, соответственно результат на [math][\dfrac+1\ldots n-1][/math] . И так далее, продвигаясь вглубь дерева.

Построение дерева

Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math] , где [math]2^k \geqslant n[/math] . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой [math]n+\dfrac+\dfrac \ldots +1 \lt 2n[/math] , где [math]n=2^k[/math] . Таким образом, структура занимает линейную память.

Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.

Реализация построения сверху:

function treeBuild(T a[], int i, int tl, int tr): // мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr) if tr - tl == 1 t[i] = a[tl] else tm = (tl + tr) / 2 // середина отрезка treeBuild(a, 2 * i + 1, tl, tm) treeBuild(a, 2 * i + 2, tm, tr) t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

Реализация построения снизу:

function treeBuild(T a[]): for i = 0 to n - 1 t[n - 1 + i] = a[i] for i = n - 2 downto 0 t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

См. также

Источники информации

Источник