Дерево отрезков python реализация
Segment Tree
import math class SegmentTree: def __init__(self, a): self.N = len(a) self.st = [0] * ( 4 * self.N ) # approximate the overall size of segment tree with array N if self.N: self.build(1, 0, self.N - 1) def left(self, idx): return idx * 2 def right(self, idx): return idx * 2 + 1 def build(self, idx, l, r): # noqa: E741 if l == r: self.st[idx] = A[l] else: mid = (l + r) // 2 self.build(self.left(idx), l, mid) self.build(self.right(idx), mid + 1, r) self.st[idx] = max(self.st[self.left(idx)], self.st[self.right(idx)]) def update(self, a, b, val): return self.update_recursive(1, 0, self.N - 1, a - 1, b - 1, val) def update_recursive(self, idx, l, r, a, b, val): # noqa: E741 """ update(1, 1, N, a, b, v) for update val v to [a,b] """ if r < a or l > b: return True if l == r: self.st[idx] = val return True mid = (l + r) // 2 self.update_recursive(self.left(idx), l, mid, a, b, val) self.update_recursive(self.right(idx), mid + 1, r, a, b, val) self.st[idx] = max(self.st[self.left(idx)], self.st[self.right(idx)]) return True def query(self, a, b): return self.query_recursive(1, 0, self.N - 1, a - 1, b - 1) def query_recursive(self, idx, l, r, a, b): # noqa: E741 """ query(1, 1, N, a, b) for query max of [a,b] """ if r < a or l > b: return -math.inf if l >= a and r return self.st[idx] mid = (l + r) // 2 q1 = self.query_recursive(self.left(idx), l, mid, a, b) q2 = self.query_recursive(self.right(idx), mid + 1, r, a, b) return max(q1, q2) def show_data(self): show_list = [] for i in range(1, N + 1): show_list += [self.query(i, i)] print(show_list) if __name__ == "__main__": A = [1, 2, -4, 7, 3, -5, 6, 11, -20, 9, 14, 15, 5, 2, -8] N = 15 segt = SegmentTree(A) print(segt.query(4, 6)) print(segt.query(7, 11)) print(segt.query(7, 12)) segt.update(1, 3, 111) print(segt.query(1, 15)) segt.update(7, 8, 235) segt.show_data()
Источник
How to Implement Segment Tree in Python?
In this tutorial, we will learn what Segment Tree is and how to implement Segment Tree in Python with some non-recursive functions. This is a very important topic in Practical Data Structures.
Segment Tree is basically a data structure. It can be used to perform range queries and updates in an easy and fastest way.
Python program to implement segment tree
To understand Segment Tree we have to take an array first.
Let’s take an array A=[1,3,5,6,7,-3,6,2] of length 8 indexed from 0 to 7 and we have to solve problems called range queries and updates.
- Range queries mean to determine the sum of different segments of the given array.
Example-sum(0,3)=1+3+5+6=15 (Here 0 and 3 represent the index no. of the given array). - update means to change the value of a specified element of the given array to a new value.
Example-If we perform an update(3,5), then the array becomes A=[1,3,5,5,7,-3,6,2] (Here 3 represents the index of the array, whose value to be changed and 5 represent the new or updated value). - After performing the update, the sum(0,3) becomes 14(1+3+5+5) because of updating the value of the element index 3.
So, We can use Segment Tree to perform both the operations(range queries and update) in O(log n) time. First of all, let us have a look at the Segment Tree of the given array :
In the above figure [L,R) indicates that left (L)is included and right(R)is excluded.
From the above image, you can see that the tree has 15 nodes in total and if you chose any one node from the parent nodes, let us suppose node 4 from the above tree then the left and right child of that node are node 8 and node 9 respectively.
So, in general, we can say that if we construct a Segment Tree for an element array total number of elements of the tree array will be (2*n-1) and the left and right child of the pth node will be at 2*p and 2*p+1 index respectively. Leaf nodes are starting from index (n) to (2*n-1). We can also observe that an element will be at index (k+n) in the segment tree array if it is kth element or k index element in the original array.
To perform range queries and updates using the Segment tree I am using three non-recursive functions. Python code of these three functions are given below:
# function to build the segmenttree array def buildTree(a): # insert leaf nodes in tree for i in range(n): tree[n + i] = a[i] # creating parent node by adding left and right child for i in range(n - 1, 0, -1): tree[i] = tree[2*i] + tree[2*i+1]
# function to update a node of the tree def updateTree(index, value): # set value at position index tree[index + n] = value index+=n # after updating the child node,update parents i = index while i > 1: #update parent by adding new left and right child tree[i//2] = tree[i] + tree[i^1] i =i//2
#function to find sum on different range def queryTree(l, r): sum = 0 #to find the sum in the range [l,r) l += n r += n while l < r: if ((l & 1)>0): sum += tree[l] l += 1 if ((r & 1)>0): r -= 1 sum += tree[r] l =l// 2 r =r// 2 return sum
To check these three non-recursive function we have to write the main function.
if __name__ == "__main__": A = [1, 2, 3, 4, 5, 6, 7,8] n = len(A) buildTree(A) print(queryTree(1, 4)) updateTree(2, 5) print(queryTree(1, 4))
Источник
Дерево отрезков
Для изучения темы “дерево отрезков” необходимо знать следующие понятия:
Дерево отрезков (Segment Tree) — это динамическая структура данных, используемая для выполнения операций над интервалами и их обновления. Оно поддерживает две операции: обновление элементов (update) в заданном диапазоне и запрос (query) на сумму элементов в заданном диапазоне.
Выполним следующую задачу: у нас есть массив, и мы хотим находить сумму элементов в определенном диапазоне.
Для этой задачи мы можем использовать дерево отрезков. Оно построено как бинарное дерево, где каждый узел представляет интервал, а значение узла — это сумма элементов в этом интервале.
Элемент суммы в дереве отрезков является суммой всех элементов в диапазоне, который он представляет.
Дерево отрезков может быть построено на базе массива чисел. Каждый узел дерева представляет диапазон элементов в массиве и хранит сумму элементов в этом диапазоне.
Реализация различных операций в дереве отрезков по сути зависит от его структуры. Однако, существует несколько операций, которые часто используются в различных задачах:
- Обновление значения в массиве: Эта операция позволяет изменять значение элемента в массиве. Обычно она реализуется с помощью рекурсивного прохода по дереву.
- Запрос на значение: Эта операция позволяет запрашивать значение элемента в массиве. Обычно она также реализуется с помощью рекурсивного прохода по дереву.
- Запрос на сумму: Эта операция позволяет запрашивать сумму значений в массиве на заданном интервале. Она обычно реализуется с помощью рекурсивного прохода по дереву и подсчета суммы
Построение дерева отрезков
Так как дерево бинарное, у каждой вершины будет до двух потомков.
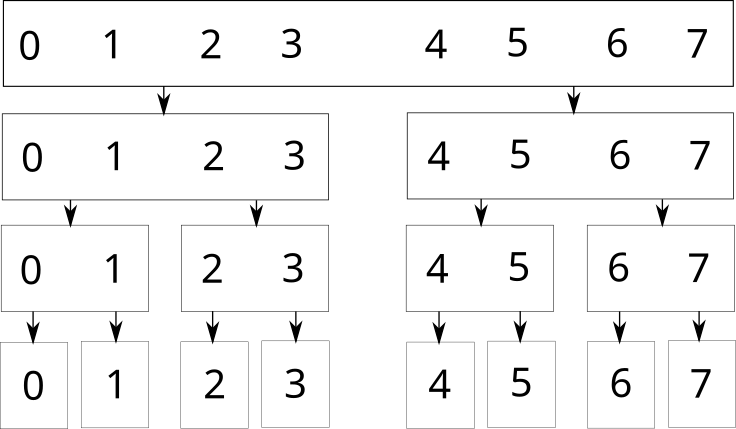
Графически это выглядит следующим образом (для массива из 8 элементов):
В самой верхней вершине зафиксирован отрезок от начала массива до последнго элемента.
Слева — лева половина от родителя ( [0 1 2 3] ). Справа — правая половина () [4 5 6 7] ). И так далее до последнего узла с отрезком из одного элемента.
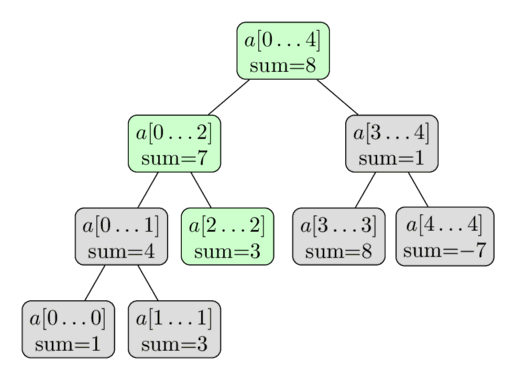
Возьмем массив a = [1, 3, -2, 8, -7] . На его базе построим дерево отрезкови запишем суммы этих отрезков в каждый узел.
Структура такого дерево выглядит следующим образом:
💡 Дерево содержит менее 2n вершин. 2*n-1
Число вершин в худшем случае оценивается суммой $n + \frac + \frac + \frac + \ldots + 1 < 2n$
Отобразим такое дерево как массив:
tree[0] = A[0:4] tree[1] = A[0:2] tree[2] = A[3:4] tree[3] = A[0:1] tree[4] = A[2:2] tree[5] = A[3:3] tree[6] = A[4:4] tree[7] = A[0:0] tree[8] = A[1:1] В данном дереве покрыты все вершины.
Имея такую структуру, в значениях вершин можно хранить различные данные, например, сумму отрезка, наименьшее/наибольшее число или другие агрегированные данные на отрезках.
Реализация дерева отрезков на Python
Так как самыми последними вершинами являются отрезки длиной == 1 . То процесс создания начинаем с них, постепенно поднимаясь на уровень выше.
💡 Дерево содержит менее 2n вершин. 💡 Нижняя виршина — длина отрезка равна 1.
def build_tree(array): n = len(array) tree = [0] * 2 * n # Дерево содержит менее **2n** вершин. for i in range(n): tree[n + i] = a[i] # самые нижние вершины дерева # добавляем родителей for i in reversed(range(n)): tree[i] = tree[2 * i] + tree[2 * i + 1] print(i, tree) >> array = [1, 3, -2, 8, -7] >> build_tree(array) 4 [0, 0, 0, 0, 1, 1, 3, -2, 8, -7] 3 [0, 0, 0, 1, 1, 1, 3, -2, 8, -7] 2 [0, 0, 2, 1, 1, 1, 3, -2, 8, -7] 1 [0, 3, 2, 1, 1, 1, 3, -2, 8, -7] 0 [3, 3, 2, 1, 1, 1, 3, -2, 8, -7] Подсчет суммы на отрезке:
Функция получает индексы исходного массива.
При создании дерева из изходного массива мы помещали каждый отдельный элемент на новый индекс [n + i] .
💡 Поэтому когда функция принимает индекс, сначала мы найдет самый нижний элемент в дереве. Он расположен в новом массиве по индексу [длина_исходного_массива + index]
# подсчет суммы на отрезке def query_tree(l, r): global tree, n sum = 0 l += n # индекс текущего элемента r += n while l r: if l % 2 == 1: # если индекс нечетный sum += tree[l] l += 1 if r % 2 == 0: sum += tree[r] r -= 1 l //= 2 # floor division. 8 // 3 = 2 r //= 2 return sum >> a = [1, 3, -2, 8, -7] >> n = len(a) >> tree = build_tree(a) >> query_tree(0, 4) # sum([1, 3, -2, 8, -7]) 3 >> query_tree(1, 3) # sum([3, -2, 8]) 9 >> query_tree(4, 4) -7 Получаем класс SegmentTree :
Функцию суммирования или любую другую можно включить в момент генерации дерева
class SegmentTree: def __init__(self, a): self.n = len(a) self.tree = [0] * 2 * self.n for i in range(self.n): self.tree[self.n + i] = a[i] for i in range(self.n - 1, 0, -1): self.tree[i] = self.tree[2*i] + self.tree[2*i+1] def calculate_sum(self, l, r): sum = 0 l += self.n r += self.n while l r: if l % 2 == 1: sum += self.tree[l] l += 1 if r % 2 == 0: sum += self.tree[r] r -= 1 l //= 2 r //= 2 return sum def find_value(self, l, r): l += self.n r += self.n while l r: if r % 2 == 0: r -= 1 else: r -= 1 l += 1 return l - self.n Шаблон класса Segment Tree
class SegmentTree: def __init__(self, data, default=0, func=max): self._default = default self._func = func self._len = len(data) self._size = _size = 1 (self._len - 1).bit_length() self.data = [default] * (2 * _size) self.data[_size:_size + self._len] = data for i in reversed(range(_size)): self.data[i] = func(self.data[i + i], self.data[i + i + 1]) def __delitem__(self, idx): self[idx] = self._default def __getitem__(self, idx): return self.data[idx + self._size] def __setitem__(self, idx, value): idx += self._size self.data[idx] = value idx >>= 1 while idx: self.data[idx] = self._func(self.data[2 * idx], self.data[2 * idx + 1]) idx >>= 1 def __len__(self): return self._len def query(self, start, stop): """func of data[start, stop)""" start += self._size stop += self._size if start==stop: return self._default res_left = res_right = self._default while start stop: if start & 1: res_left = self._func(res_left, self.data[start]) start += 1 if stop & 1: stop -= 1 res_right = self._func(self.data[stop], res_right) start >>= 1 stop >>= 1 return self._func(res_left, res_right) def __repr__(self): return "SegmentTree( )".format(self.data) Метод build_tree строит дерево отрезков, а query позволяет выполнять операции запроса.
Ресурсы
Источник